Referencias
https://cran.r-project.org/web/packages/data.tree/vignettes/data.tree.html
- Más ejemplos de data.tree (se resuelven problemas: árbol de decisión, selección de genes, …)
Vídeo de youtube en el que se explican los árboles de decisión para clasificación
Resolviendo árboles de decisión con “radiant.models”
Introducción
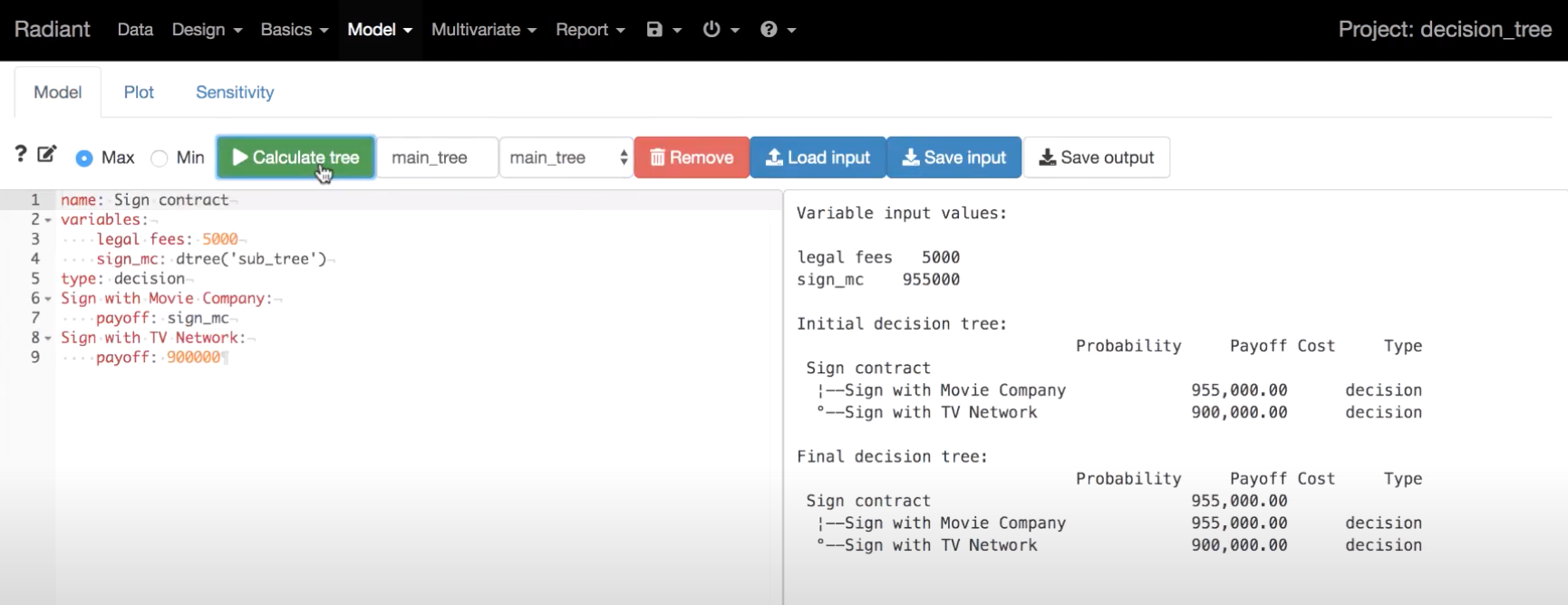
En las siguientes capturas puede verse cómo se resuelve desde “Radiant” (“Models-Decision”) un problema de árboles de decisión.
El primer paso será escribir los datos asociados al árbol de decisión. Radiant usa la estructura del paquete “data.tree” (ver más en la referencia citada al inicio de este documento). Y al pulsar sobre el botón de “Calculate tree” se obtiene la solución en formato texto, cómo puede verse en la captura a la derecha. El árbol se puede definir cómo de “Ganancias” (“Max”) o de “Costos” (“Min”).
Se pueden definir los diferentes elementos de un modelo de árboles de decisión:
“name”: nombre del árbol de decisión planteado.
“variables”: se pueden definir distintas variables o valores del modelo que pueden variar y aparecer en distintas posiciones. Por ejemplo, se pueden usar luego para un estudio de análisis de sensibilidad.
“type”: tipo de nodo:
“decision”: para representar alternativas o decisiones entre las que elegir.
- “cost”: se pueden asociar a las distintas alternativas.
- “type: chance”. Nodos Hijos de riesgo.
- “payoff”: valor asociado en la tabla de pagos o valoraciones a esa decisión. Todos los nodos terminales tienen que tener un valor “payoff”.
“chance”: para representar los nodos de riesgo o los estados de la naturaleza con naturaleza probabilística.
- “p”: probabilidad asociada a ese nodo de riesgo (todas las probabilidades desde un nodo “chance” tienen que sumar 1 y deben ser valores entre 0 y 1).
- “payoff”: valor asociado en la tabla de pagos o valoraciones a ese nodo de riesgo. Todos los nodos terminales tienen que tener un valor “payoff”.
Nota 1: Cada una de las alternativas o nodos de riesgo se les da nombre colocando estos en la misma columna que la definición “type”.
Nota 2: se usan “4 espacios en blanco” para indentar cada subnivel en el árbol de decisión.
Nota 3: la variable “legal fees” se ha utilizado únicamente como costo asociado a la alternativa “Sign with Movie Company”.
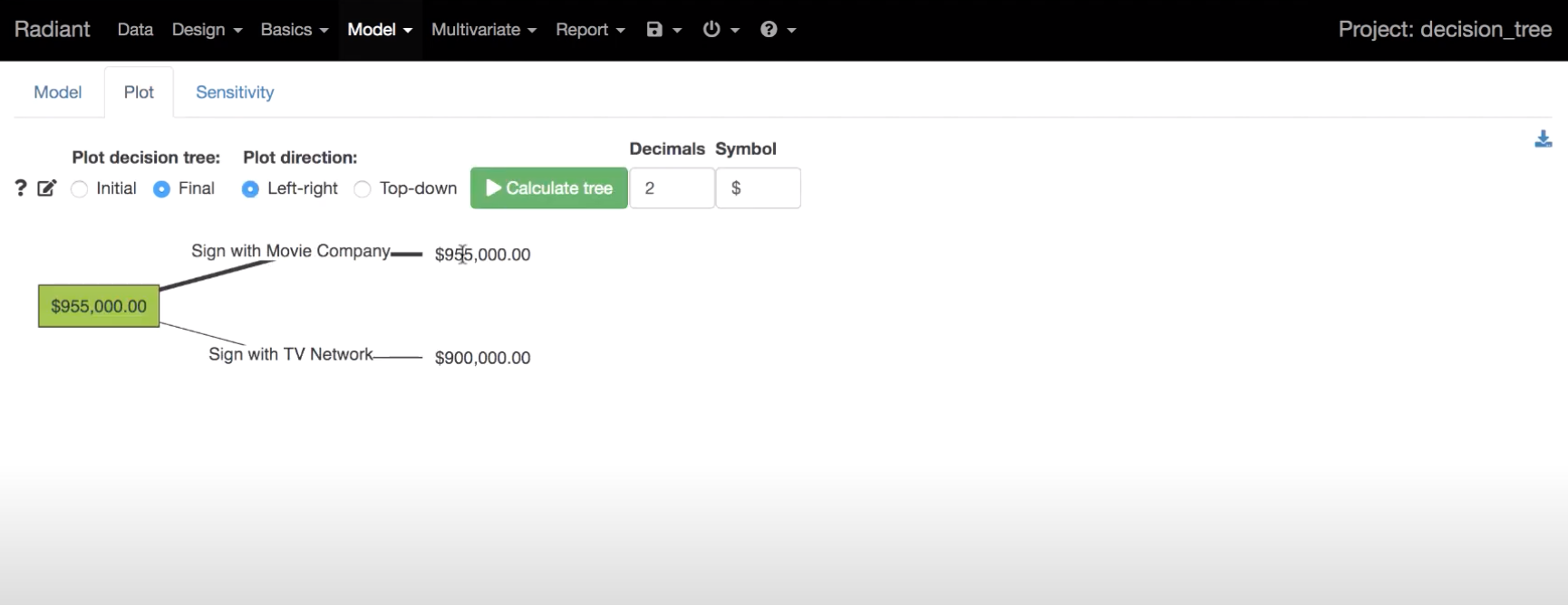
En el apartado “Plot” de Radiant puede verse una representación gráfica del problema de dos modos: (a) de arriba a abajo o (b) de izquierda a derecha.
En esta captura se muestra el árbol de decisión de arriba a abajo antes de resolverse (“Initial”).
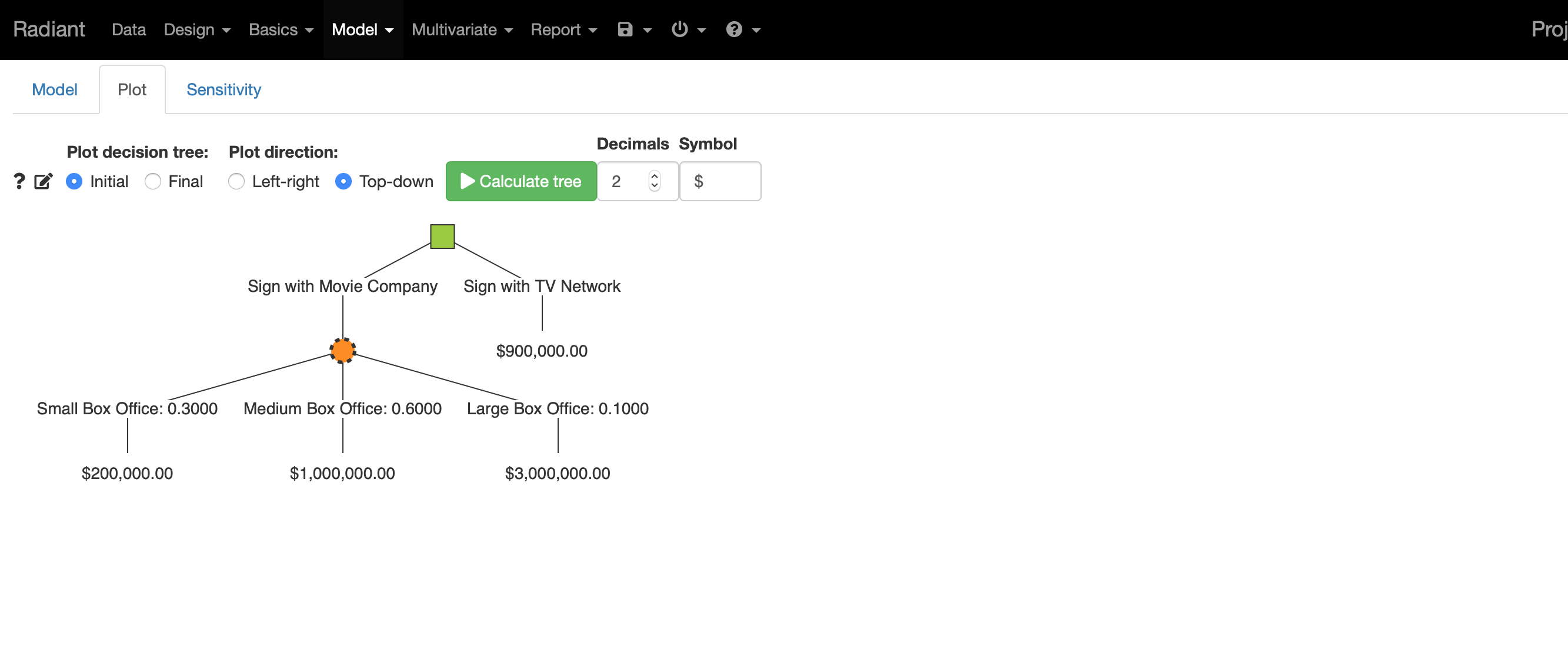
En esta captura se muestra el árbol de decisión de arriba a abajo después de resolverse (“Final”).
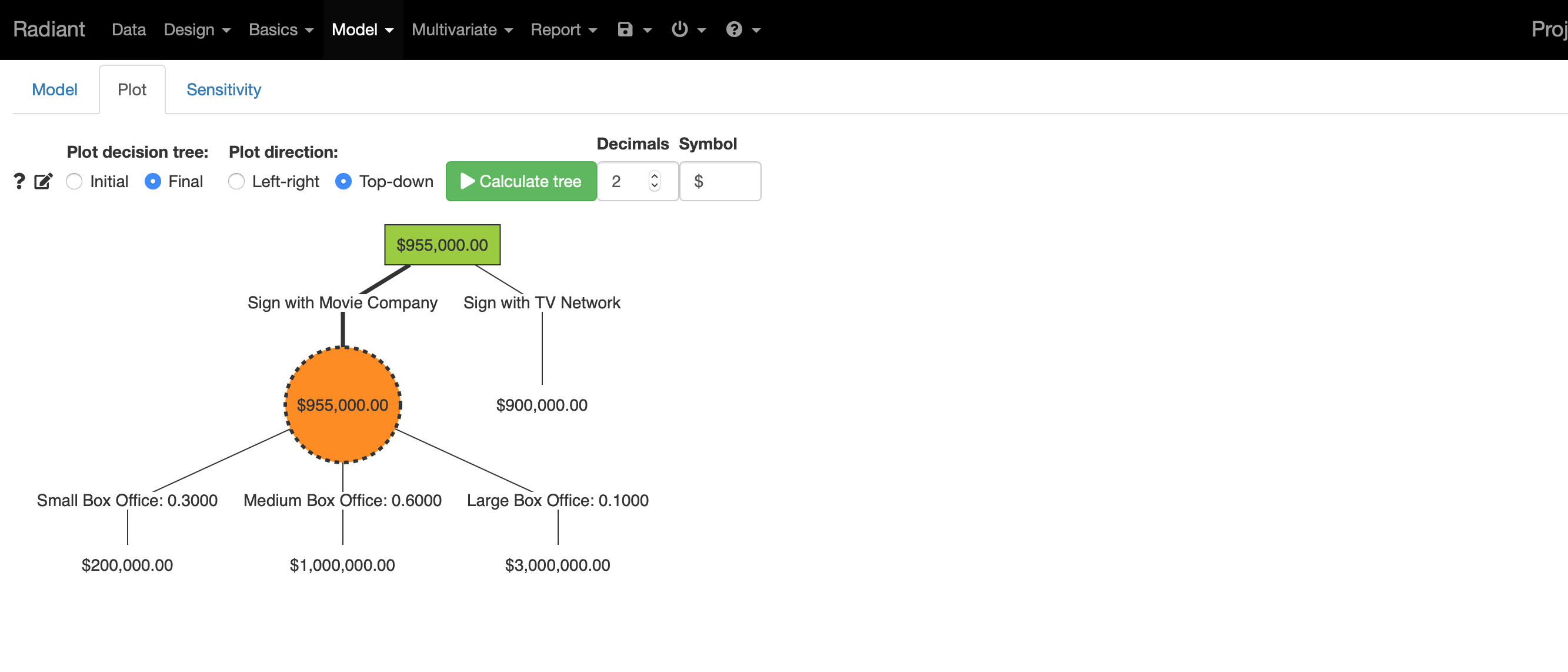
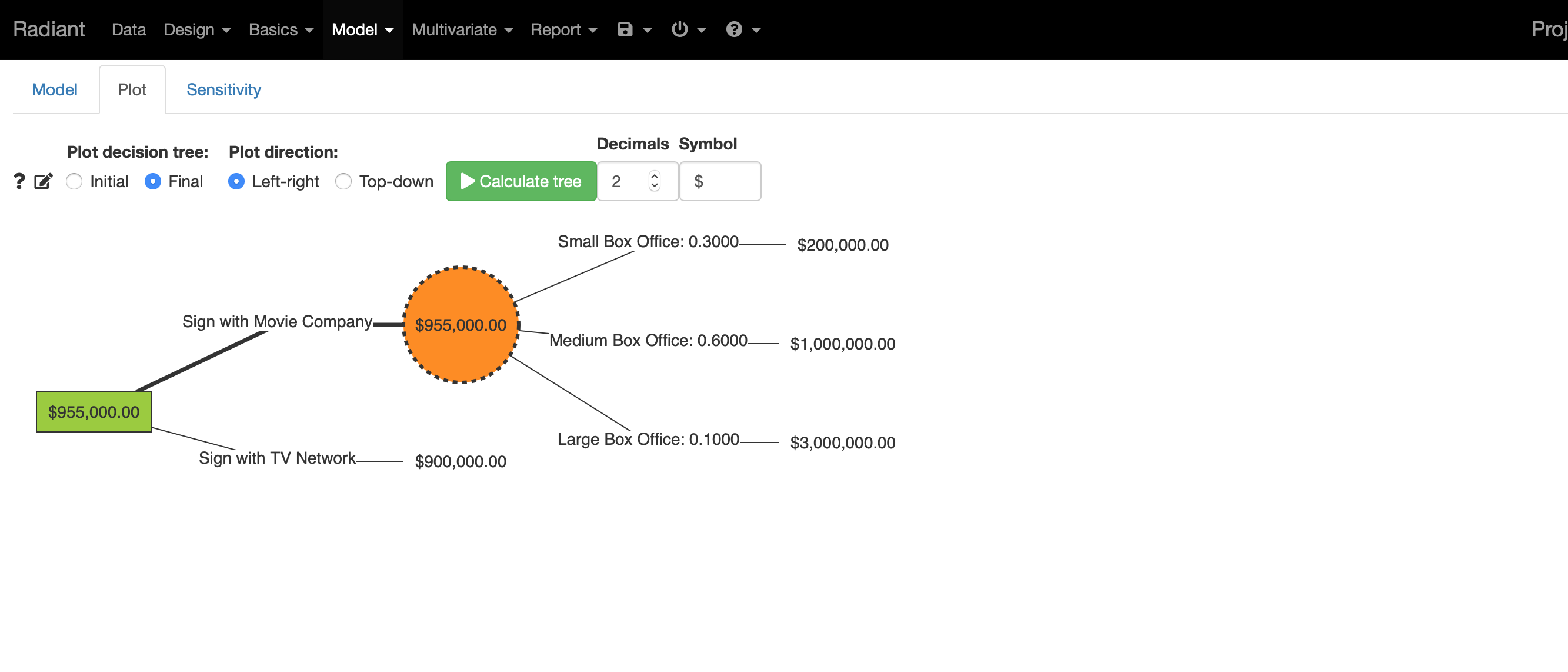
En esta captura se muestra el árbol de decisión de izquierda a derecha después de resolverse (“Final”).
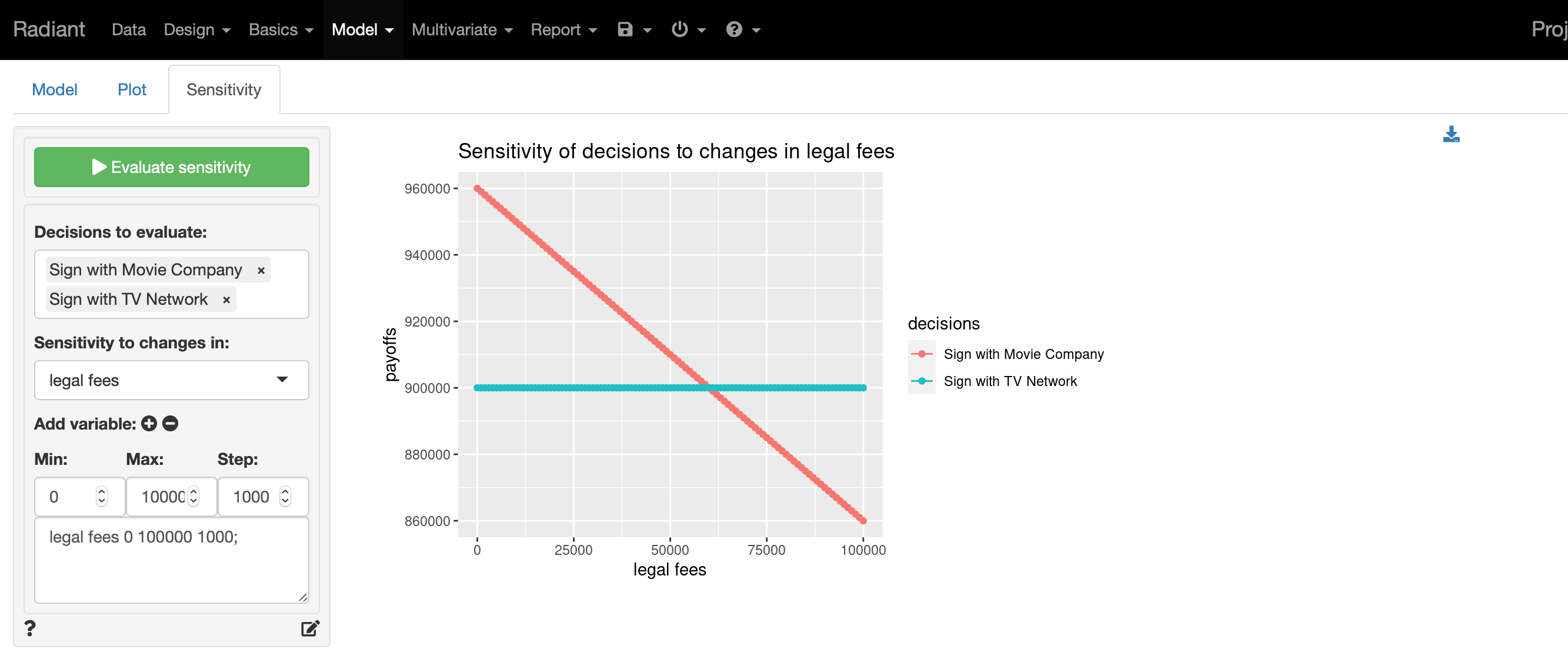
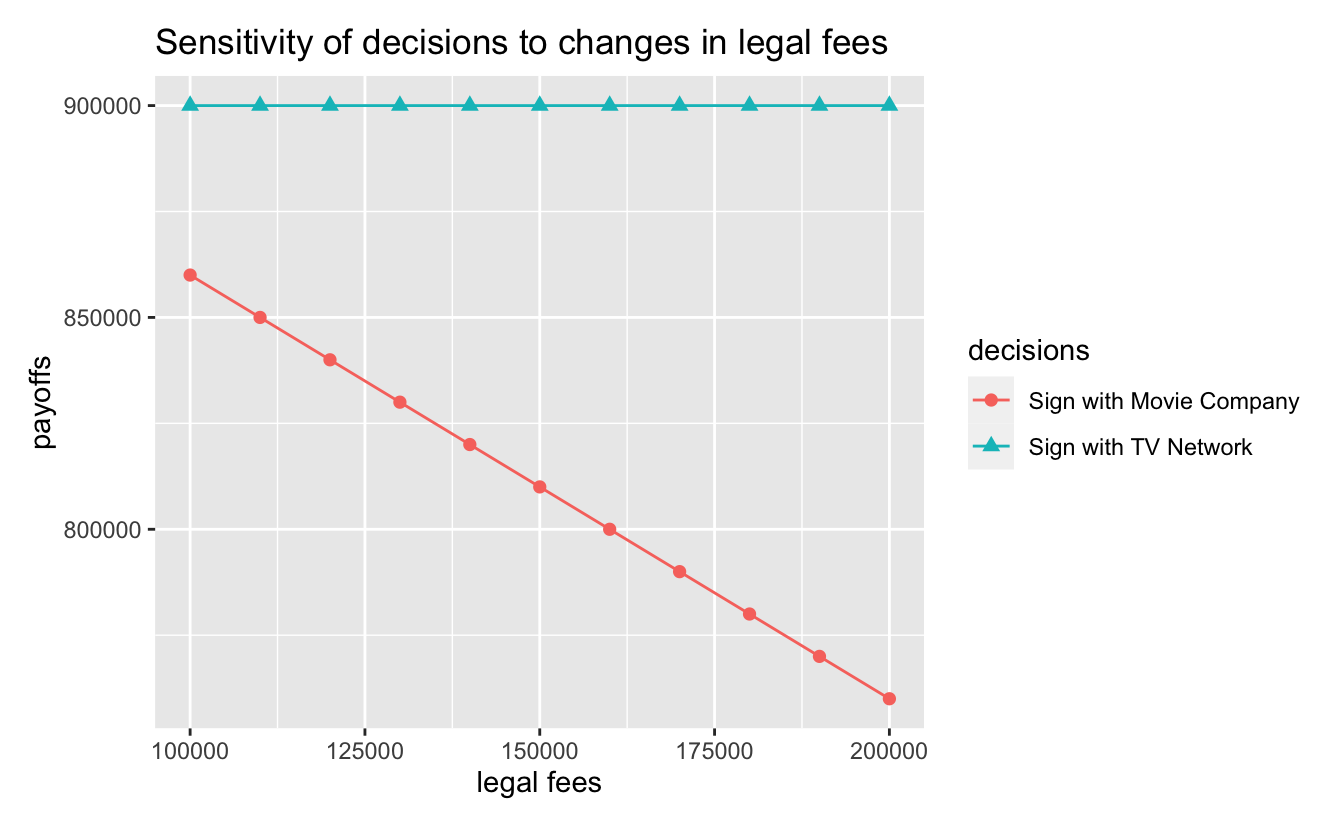
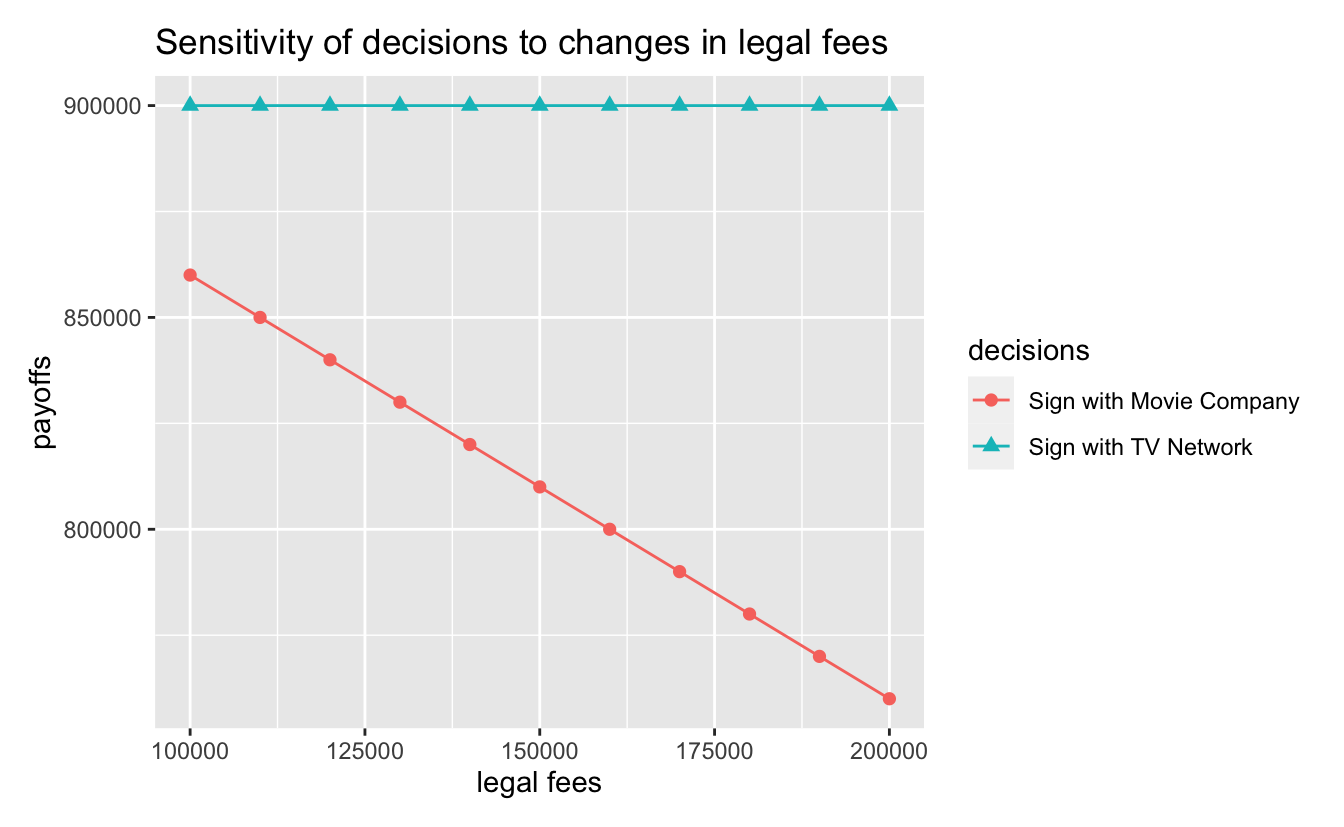
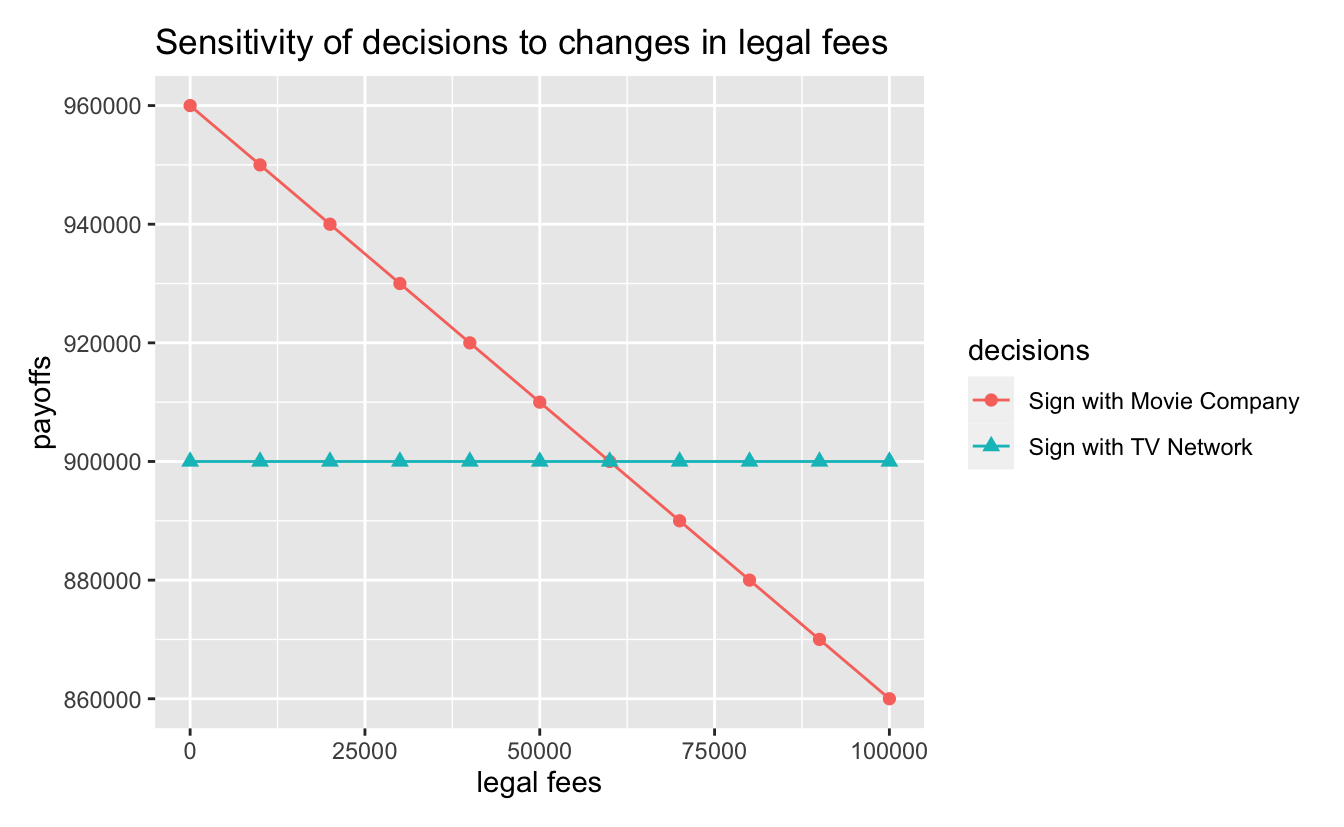
En el apartado “Sensitivity” se puede realizar un análisis de sensibilidad sobre alguna de las variables definidas en el árbol de decisión.
En esta captura se muestra cómo cambia el valor de cada una de las alternativas o decisiones (nodos: “decision”) al modificar la variable “legal fees” (que se ha definido como un costo)
Ayuda para crear fichero yaml del árbol de decisión (radiant)
Reglas para la entrada del árbol de decisiones
Siempre comience con un nombre de árbol (por ejemplo, name: Mi árbol)
La segunda línea debe comenzar una sección de variables o una definición de nodo (es decir,
type: chanceotype: decisión)Todas las líneas deben tener:. Para los nodos
namelos:finalizan la línea. Para todas las demás líneas, asigna un valor. Específicamente, asigna un nombre (p. Ej.,name: Mi árbol), un nodotype(p. ej.,type: decision), unavariable(p. ej.,Honorarios legales: 5000) o un número (p. ej.,payoff: 100,p: 0.1,cost: 10).Un nodo
typedebe ir seguido en la siguiente línea por un nodo nombre (por ejemplo,Cancelar pedidos:).Use solo letras y espacios en los nombres de los nodos (es decir, sin símbolos).
La línea que sigue al nombre de un nodo siempre debe tener sangría.
Los nodos finales (o terminales o de salida) deben tener una recompensa (por ejemplo,
payoff: 100).Si están vinculados a un nodo de azar, los nodos terminales deben tener una probabilidad (por ejemplo,
p: 0.4) y una recompensapayoff.
Para referenciar a otro “subárbol” se debe usar la función dtree en la sección “variables” y el nombre del “subárbol”. Por ejemplo, se supone que se quiere incluir un árbol “tuesday_tree” que evalúa una decisión sobre precios el martes en un árbol que evalúa la decisión sobre precios el lunes. El inicio de la sección “variables” debe escribirse cómo se muestra a continuación:
variables:
tuesday_emv: dtree("tuesday_tree")En el árbol del lunes se debería referenciar a “tuesday_emw” en el apartado donde se necesite el EMV (valor monetario esperado) de la decisión de precios del martes.
En las siguientes capturas se ve un ejemplo mucho más detallado del proceso de solución con la inclusión de subárboles.
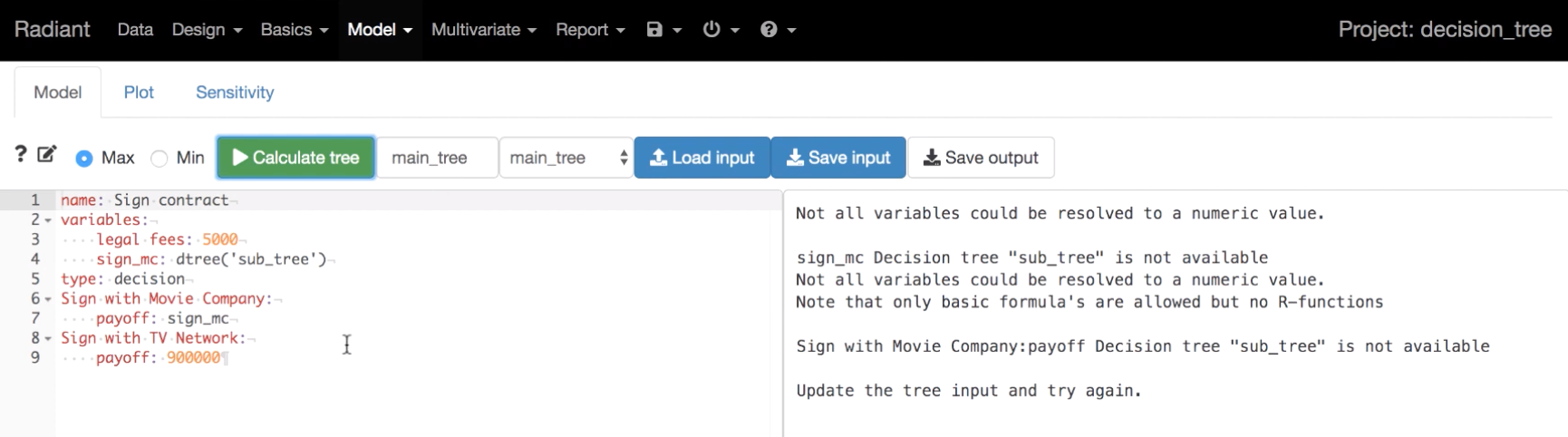
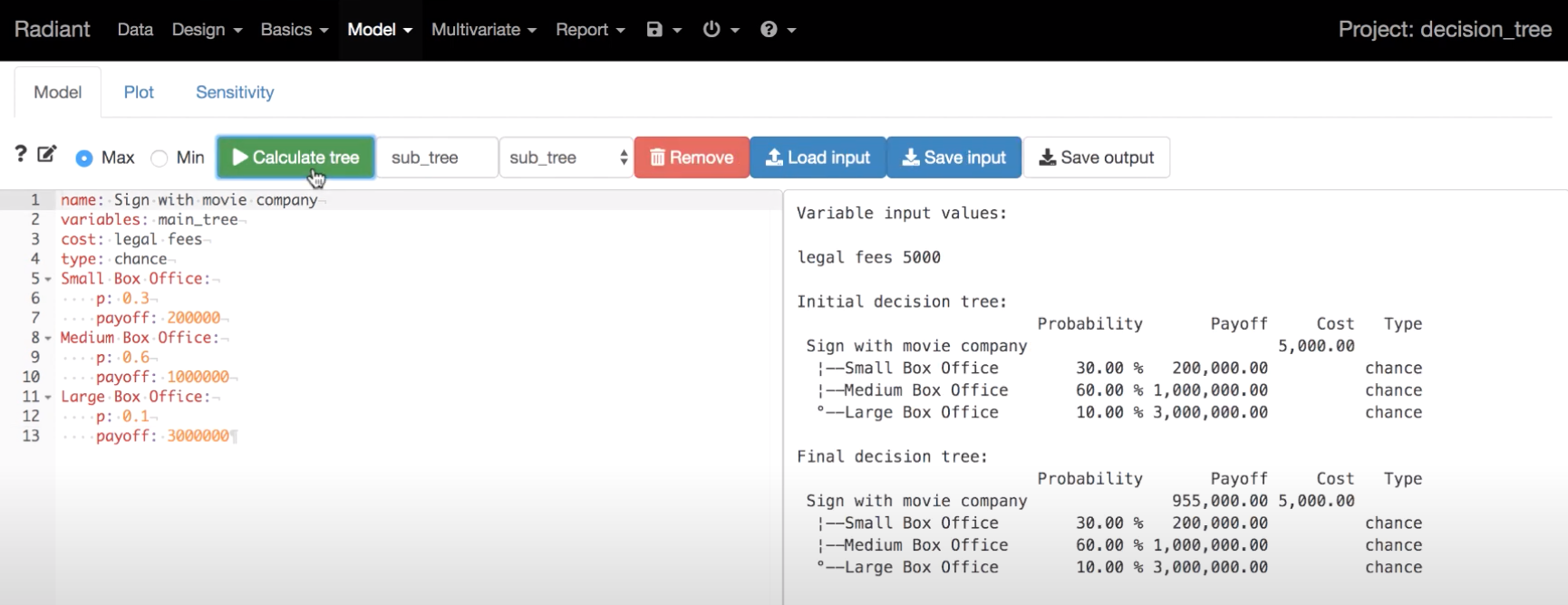
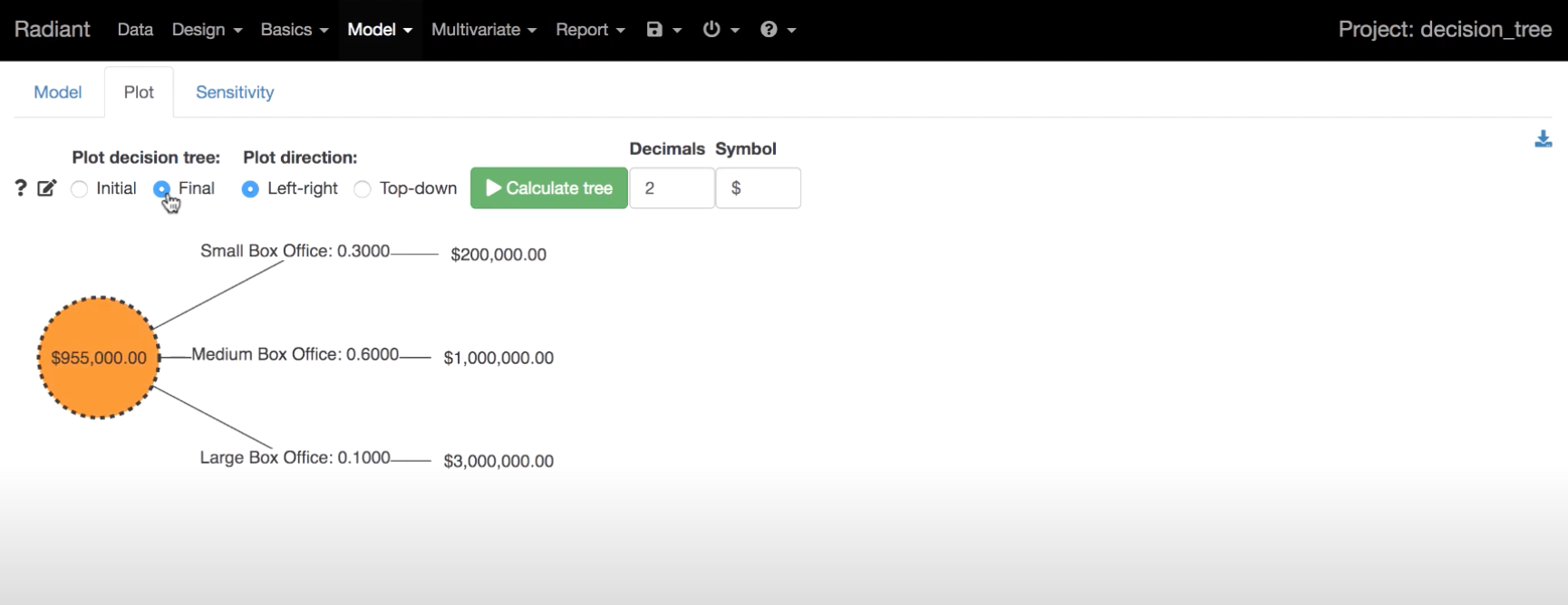

Código generado por Radiant
Sign_contract = "
name: Sign contract
variables:
legal fees: 5000
P(small): 0.3
P(medium): 0.6
P(large): 1 - P(small) - P(medium)
type: decision
Sign with Movie Company:
cost: legal fees
type: chance
Small Box Office:
p: P(small)
payoff: 200000
Medium Box Office:
p: P(medium)
payoff: 1000000
Large Box Office:
p: P(large)
payoff: 3000000
Sign with TV Network:
payoff: 900000
" También se podría guardar en un fichero con extensión “yaml” y cargarlo con ayuda de las funciones del paquete R “yaml”.
writeLines(Sign_contract,con = "signcontract.yaml")Para leerlo, se podría utilizar:
Sign_contract2 = "signcontract.yaml"
obj_ym = yaml::yaml.load_file(Sign_contract2)
yaml::as.yaml(obj_ym) %>% cat()name: Sign contract
variables:
legal fees: 5000
P(small): 0.3
P(medium): 0.6
P(large): 1 - P(small) - P(medium)
type: decision
Sign with Movie Company:
cost: legal fees
type: chance
Small Box Office:
p: P(small)
payoff: 200000
Medium Box Office:
p: P(medium)
payoff: 1000000
Large Box Office:
p: P(large)
payoff: 3000000
Sign with TV Network:
payoff: 900000A continuación se recoge el código que genera Radiant al pulsar sobre el icono de “escribir código”:
suppressMessages(library(radiant.model))
result <- dtree(yl = "Sign_contract")
summary(result, input = TRUE, output = FALSE)Decision tree input:
name: Sign contract
variables:
legal fees: 5000
P(small): 0.3
P(medium): 0.6
P(large): 1 - P(small) - P(medium)
type: decision
Sign with Movie Company:
cost: legal fees
type: chance
Small Box Office:
p: P(small)
payoff: 200000
Medium Box Office:
p: P(medium)
payoff: 1000000
Large Box Office:
p: P(large)
payoff: 3000000
Sign with TV Network:
payoff: 900000plot(result) %>% render()result <- dtree(yl = "Sign_contract")
summary(result, input = TRUE, output = FALSE)Decision tree input:
name: Sign contract
variables:
legal fees: 5000
P(small): 0.3
P(medium): 0.6
P(large): 1 - P(small) - P(medium)
type: decision
Sign with Movie Company:
cost: legal fees
type: chance
Small Box Office:
p: P(small)
payoff: 200000
Medium Box Office:
p: P(medium)
payoff: 1000000
Large Box Office:
p: P(large)
payoff: 3000000
Sign with TV Network:
payoff: 900000sensitivity(
result,
vars = "legal fees 100000 200000 10000",
decs = c("Sign with Movie Company", "Sign with TV Network"),
custom = FALSE
)
plot(result, final = TRUE, orient = "TD") %>% render()result <- dtree(yl = "Sign_contract")
summary(result, input = TRUE, output = FALSE)Decision tree input:
name: Sign contract
variables:
legal fees: 5000
P(small): 0.3
P(medium): 0.6
P(large): 1 - P(small) - P(medium)
type: decision
Sign with Movie Company:
cost: legal fees
type: chance
Small Box Office:
p: P(small)
payoff: 200000
Medium Box Office:
p: P(medium)
payoff: 1000000
Large Box Office:
p: P(large)
payoff: 3000000
Sign with TV Network:
payoff: 900000sensitivity(
result,
vars = "legal fees 100000 200000 10000",
decs = c("Sign with Movie Company", "Sign with TV Network"),
custom = FALSE
)
plot(result, orient = "TD") %>% render()result <- dtree(yl = "Sign_contract")
summary(result, input = TRUE, output = FALSE)Decision tree input:
name: Sign contract
variables:
legal fees: 5000
P(small): 0.3
P(medium): 0.6
P(large): 1 - P(small) - P(medium)
type: decision
Sign with Movie Company:
cost: legal fees
type: chance
Small Box Office:
p: P(small)
payoff: 200000
Medium Box Office:
p: P(medium)
payoff: 1000000
Large Box Office:
p: P(large)
payoff: 3000000
Sign with TV Network:
payoff: 900000sensitivity(
result,
vars = "legal fees 0 100000 10000",
decs = c("Sign with Movie Company", "Sign with TV Network"),
custom = FALSE
)
plot(result, orient = "TD") %>% render()Ejemplo de árbol de decisión con información imperfecta (bayesiano)
EjemploBayesiano = "name: open new store
variables:
fixed cost: 2000000
popup cost: 500000
P(S): 0.6
P(F): 1 - P(S)
P(+|S): 0.8
P(-|S): 1 - P(+|S)
P(-|F): 0.9
P(+|F): 1 - P(-|F)
P(+): P(+|S) * P(S) + P(+|F) * P(F)
P(-): P(-|F) * P(F) + P(-|S) * P(S)
P(S|+): P(+|S) * P(S) / P(+)
P(F|+): 1 - P(S|+)
P(F|-): P(-|F) * P(F) / P(-)
P(S|-): 1 - P(F|-)
payoff_S: 5000000
payoff_F: -1000000
type: decision
open:
cost: fixed cost
type: chance
success:
p: P(S)
payoff: payoff_S
failure:
p: P(F)
payoff: payoff_F
popup test:
cost: popup cost
type: chance
test positive:
p: P(+)
type: decision
open:
cost: fixed cost
type: chance
success:
p: P(S|+)
payoff: payoff_S
failure:
p: P(F|+)
payoff: payoff_F
not open:
payoff: 0
test negative:
p: P(-)
type: decision
open:
cost: fixed cost
type: chance
success:
p: P(S|-)
payoff: payoff_S
failure:
p: P(F|-)
payoff: payoff_F
not open:
payoff: 0
not open:
payoff: 0
"result <- dtree(yl = "EjemploBayesiano")
summary(result, input = TRUE, output = FALSE)Decision tree input:
name: open new store
variables:
fixed cost: 2000000
popup cost: 500000
P(S): 0.6
P(F): 1 - P(S)
P(+|S): 0.8
P(-|S): 1 - P(+|S)
P(-|F): 0.9
P(+|F): 1 - P(-|F)
P(+): P(+|S) * P(S) + P(+|F) * P(F)
P(-): P(-|F) * P(F) + P(-|S) * P(S)
P(S|+): P(+|S) * P(S) / P(+)
P(F|+): 1 - P(S|+)
P(F|-): P(-|F) * P(F) / P(-)
P(S|-): 1 - P(F|-)
payoff_S: 5000000
payoff_F: -1000000
type: decision
open:
cost: fixed cost
type: chance
success:
p: P(S)
payoff: payoff_S
failure:
p: P(F)
payoff: payoff_F
popup test:
cost: popup cost
type: chance
test positive:
p: P(+)
type: decision
open:
cost: fixed cost
type: chance
success:
p: P(S|+)
payoff: payoff_S
failure:
p: P(F|+)
payoff: payoff_F
not open:
payoff: 0
test negative:
p: P(-)
type: decision
open:
cost: fixed cost
type: chance
success:
p: P(S|-)
payoff: payoff_S
failure:
p: P(F|-)
payoff: payoff_F
not open:
payoff: 0
not open:
payoff: 0Se puede mostrar las salidas y no las entradas:
summary(result, input = FALSE, output = TRUE)Variable input values:
fixed cost 2000000.00000000
popup cost 500000.00000000
P(S) 0.60000000
P(F) 0.40000000
P(+|S) 0.80000000
P(-|S) 0.20000000
P(-|F) 0.90000000
P(+|F) 0.10000000
P(+) 0.52000000
P(-) 0.48000000
P(S|+) 0.92307692
P(F|+) 0.07692308
P(F|-) 0.75000000
P(S|-) 0.25000000
payoff_S 5000000.00000000
payoff_F -1000000.00000000
Initial decision tree:
Probability Payoff Cost Type
open new store
¦--open 2,000,000.00 decision
¦ ¦--success 60.00 % 5,000,000.00 chance
¦ °--failure 40.00 % -1,000,000.00 chance
¦--popup test 500,000.00 decision
¦ ¦--test positive 52.00 % chance
¦ ¦ ¦--open 2,000,000.00 decision
¦ ¦ ¦ ¦--success 92.31 % 5,000,000.00 chance
¦ ¦ ¦ °--failure 7.69 % -1,000,000.00 chance
¦ ¦ °--not open 0.00 decision
¦ °--test negative 48.00 % chance
¦ ¦--open 2,000,000.00 decision
¦ ¦ ¦--success 25.00 % 5,000,000.00 chance
¦ ¦ °--failure 75.00 % -1,000,000.00 chance
¦ °--not open 0.00 decision
°--not open 0.00 decision
Final decision tree:
Probability Payoff Cost Type
open new store 820,000.00
¦--open 600,000.00 2,000,000.00 decision
¦ ¦--success 60.00 % 5,000,000.00 chance
¦ °--failure 40.00 % -1,000,000.00 chance
¦--popup test 820,000.00 500,000.00 decision
¦ ¦--test positive 52.00 % 2,538,461.54 chance
¦ ¦ ¦--open 2,538,461.54 2,000,000.00 decision
¦ ¦ ¦ ¦--success 92.31 % 5,000,000.00 chance
¦ ¦ ¦ °--failure 7.69 % -1,000,000.00 chance
¦ ¦ °--not open 0.00 decision
¦ °--test negative 48.00 % 0.00 chance
¦ ¦--open -1,500,000.00 2,000,000.00 decision
¦ ¦ ¦--success 25.00 % 5,000,000.00 chance
¦ ¦ °--failure 75.00 % -1,000,000.00 chance
¦ °--not open 0.00 decision
°--not open 0.00 decisionSe resuelve y se muestran los resultados de forma gráfica:
plot(result, final = TRUE) %>% render()Problemas de árboles de decisión
Para instalar los ejemplos de radiant ejecutar:
usethis::use_course("https://www.dropbox.com/sh/bit4p1ffbkb2dgh/AACm1RVy2BxBDiVbjoLiN5_Ea?dl=1")Información obtenida de: <https://radiant-rstats.github.io/docs/model/dtree.html>{target=“_blank”}.
Problema 1 (de radiant)
Eres el propietario de Radycal Kicks y estás decidiendo si abrir una nueva tienda. Ha aprendido que hay una ubicación disponible en un distrito de moda, pero debido a los altos alquileres es una propuesta arriesgada. El costo fijo de abrir la tienda es de $ 2 millones. Según el desempeño histórico de su negocio y este distrito, cree que hay un 60% de posibilidades de que la tienda tenga éxito y gane $ 5 millones en el futuro, y un 40% de posibilidades de que sea un fracaso y pierda $ 1 millón en el futuro (estas ganancias y las pérdidas se suman al costo fijo inicial de apertura de la tienda). ¿Cuál es la estrategia óptima y cuál es el valor monetario esperado (VME) asociado con su estrategia?
SOLUCIÓN.
From Example 1 I know that if I open the store, I need to pay $ 2,000,000 for fixed costs and then there are two possible scenarios: success or failure. These are not decisions but outcomes that can happen with certain probabilities. That means we need to use Chance as the node type. I specified the probability and payoff for each scenario accordingly. The payoff for not open is $ 0
Please note that you don’t need to write down all the details of how you constructed the tree in your own report. We can already see the relevant information from the structure in the output.
Analysis of decision tree output:
The thicker line in the final plot indicates the optimal strategy. We concluded that the optimal strategy for the scenrio described in example 1 is to open the store. The EMV associated with this strategy is $600,000.
ej01 = "
name: open a new store
type: decision
open:
cost: 2000000
type: chance
success:
p: 0.6
payoff: 5000000
failure:
p: 0.4
payoff: -1000000
not open:
payoff: 0
"
result <- dtree(yl = "ej01")
summary(result, input = TRUE, output = FALSE)Decision tree input:
name: open a new store
type: decision
open:
cost: 2000000
type: chance
success:
p: 0.6
payoff: 5000000
failure:
p: 0.4
payoff: -1000000
not open:
payoff: 0El resultado gráfico es:
plot(result, final = TRUE) %>% render()Problema 2 (de radiant)
Es actor y le gustaría firmar un contrato con una compañía cinematográfica o una cadena de televisión. Si firma con una compañía de películas, debe pagar $ 5,000 por los honorarios legales. Habrá un 30% de posibilidades de tener una taquilla pequeña y ganar $ 200.000, un 60% de posibilidades de tener una taquilla mediana con una recompensa igual a $ 1.000.000 y un 10% de posibilidades de tener una gran taquilla y obtener $ 3.000.000. Si decide firmar el contrato con las cadenas de televisión, su pago será de $ 900,000. ¿Qué es EMV de firmar el contrato con la compañía cinematográfica? ¿Cuál es tu estrategia óptima?
SOLUCIÓN:
ej02 = "
name: Sign contract
variables:
legal fees: 5000
type: decision
Sign with Movie Company:
cost: legal fees
type: chance
Small Box Office:
p: 0.3
payoff: 200000
Medium Box Office:
p: 0.6
payoff: 1000000
Large Box Office:
p: 0.1
payoff: 3000000
Sign with TV Network:
payoff: 900000
"
result <- dtree(yl = "ej02")
summary(result, input = TRUE, output = FALSE)Decision tree input:
name: Sign contract
variables:
legal fees: 5000
type: decision
Sign with Movie Company:
cost: legal fees
type: chance
Small Box Office:
p: 0.3
payoff: 200000
Medium Box Office:
p: 0.6
payoff: 1000000
Large Box Office:
p: 0.1
payoff: 3000000
Sign with TV Network:
payoff: 900000La solución final puede verse resaltada en el gráfico del árbol de decisión:
plot(result, final = TRUE) %>% render()Problema 3 (de radiant)
Eres el propietario de Radycal Kicks y estás decidiendo si abrir una nueva tienda. Cree que hay un 60% de posibilidades de que la tienda tenga éxito. Ahora se le ofrece administrar una tienda emergente a corto plazo para evaluar mejor el desempeño de la tienda en el distrito. La ejecución de una tienda emergente ayuda a identificar si la ubicación tendrá éxito o no. Cree que la prueba emergente identificará correctamente las ubicaciones exitosas el 80% del tiempo e identificará correctamente las fallas el 90% del tiempo. Dado que el resultado de la prueba emergente es exitoso, ¿cuál es la probabilidad de que una tienda real tenga éxito?
SOLUCIÓN.
Está resuelto en el apartado anterior en el que se explica cómo trabajar con información imperfecta, en la parte en la que se calculan las probabilidades condicionadas.
Problema 4 (de radiant)
Continuación del Ejemplo 1. Ahora, el propietario del espacio minorista le ofrece la posibilidad de administrar una tienda emergente a corto plazo para evaluar mejor el desempeño de la tienda en el distrito. Hacerlo costará $ 500,000 adicionales pero le permitirá adquirir información potencialmente útil. La ejecución de una tienda emergente ayuda a identificar si la ubicación tendrá éxito o no. Cree que la prueba emergente identificará correctamente las ubicaciones exitosas el 80% del tiempo e identificará correctamente las fallas el 90% del tiempo. ¿Cuál es la estrategia óptima? ¿Cuál es el EMV asociado a su estrategia?
SOLUCIÓN.
Está resuelto en el apartado anterior en el que se explica cómo trabajar con información imperfecta, en la parte en la que se trabaja con el árbol que utiliza las probabilidades condicionadas.
Resolución en vídeo
Estos últimos problemas son árboles de decisión con información imperfecta (bayesianos). Se puede ver como introducir estos problemas en radiant en los siguientes vídeos:
Resolviendo con el paquete “data.tree”
En primer lugar, se cargan los datos (en este caso desde un fichero yaml):
fileName <- system.file("extdata", "jennylind.yaml", package="data.tree")
cat(readChar(fileName, file.info(fileName)$size))name: Jenny Lind
type: decision
Sign with Movie Company:
type: chance
Small Box Office:
type: terminal
p: 0.3
payoff: 200000
Medium Box Office:
type: terminal
p: 0.6
payoff: 1000000
Large Box Office:
type: terminal
p: 0.1
payoff: 3000000
Sign with TV Network:
type: chance
Small Box Office:
type: terminal
p: 0.3
payoff: 900000
Medium Box Office:
type: terminal
p: 0.6
payoff: 900000
Large Box Office:
type: terminal
p: 0.1
payoff: 900000Se convierte a un objeto de tipo “data.tree”:
library(data.tree)
library(yaml)
lol <- yaml.load_file(fileName)
jl <- as.Node(lol)
print(jl, "type", "payoff", "p") levelName type payoff p
1 Jenny Lind decision NA NA
2 ¦--Sign with Movie Company chance NA NA
3 ¦ ¦--Small Box Office terminal 200000 0.3
4 ¦ ¦--Medium Box Office terminal 1000000 0.6
5 ¦ °--Large Box Office terminal 3000000 0.1
6 °--Sign with TV Network chance NA NA
7 ¦--Small Box Office terminal 900000 0.3
8 ¦--Medium Box Office terminal 900000 0.6
9 °--Large Box Office terminal 900000 0.1El proceso de cálculo se iniciaría con el siguiente código (se define la función de pago y se aplica al árbol. Tenga en cuenta que se usa el recorrido desde el final hasta el principio: “post-order”, lo que significa que se calcula el árbol desde la hoja hasta la raíz)
payoff <- function(node) {
if (node$type == 'chance')
node$payoff <- sum(sapply(node$children, function(child) child$payoff * child$p))
else if (node$type == 'decision')
node$payoff <- max(sapply(node$children, function(child) child$payoff))
}
jl$Do(payoff, traversal = "post-order", filterFun = isNotLeaf)Se puede ver los resultados:
print(jl, "type", "payoff", "p") levelName type payoff p
1 Jenny Lind decision 960000 NA
2 ¦--Sign with Movie Company chance 960000 NA
3 ¦ ¦--Small Box Office terminal 200000 0.3
4 ¦ ¦--Medium Box Office terminal 1000000 0.6
5 ¦ °--Large Box Office terminal 3000000 0.1
6 °--Sign with TV Network chance 900000 NA
7 ¦--Small Box Office terminal 900000 0.3
8 ¦--Medium Box Office terminal 900000 0.6
9 °--Large Box Office terminal 900000 0.1A continuación, se define la función “decision()” (observar que se filtra sobre nodos de decisión):
decision <- function(x) {
po <- sapply(x$children, function(child) child$payoff)
x$decision <- names(po[po == x$payoff])
}
jl$Do(decision, filterFun = function(x) x$type == 'decision')Se muestra la información actual:
print(jl, "decision","type", "payoff", "p") levelName decision type payoff p
1 Jenny Lind Sign with Movie Company decision 960000 NA
2 ¦--Sign with Movie Company chance 960000 NA
3 ¦ ¦--Small Box Office terminal 200000 0.3
4 ¦ ¦--Medium Box Office terminal 1000000 0.6
5 ¦ °--Large Box Office terminal 3000000 0.1
6 °--Sign with TV Network chance 900000 NA
7 ¦--Small Box Office terminal 900000 0.3
8 ¦--Medium Box Office terminal 900000 0.6
9 °--Large Box Office terminal 900000 0.1Representar gráficamente el árbol de decisión
Se representará con ayuda del paquete “DiagrammeR”. Se crean funciones de estilo para los distintos elementos:
GetNodeLabel <- function(node)
switch(node$type,
terminal = paste0( '$ ', format(node$payoff, scientific = FALSE, big.mark = ",")),
paste0('ER\n', '$ ', format(node$payoff, scientific = FALSE, big.mark = ",")))
GetEdgeLabel <- function(node) {
if (!node$isRoot && node$parent$type == 'chance') {
label = paste0(node$name, " (", node$p, ")")
} else {
label = node$name
}
return (label)
}
GetNodeShape <- function(node)
switch(node$type, decision = "box",
chance = "circle",
terminal = "none")
SetEdgeStyle(jl, fontname = 'helvetica', label = GetEdgeLabel)
SetNodeStyle(jl, fontname = 'helvetica', label = GetNodeLabel, shape = GetNodeShape)Se observa que fontname es inherente a todos los hijos, mientras, por ejemplo, el argumento label es una función, se llama sobre cada nodo hijo inherente.
Otra alternativa es definir el estilo por nodo:
jl$Do(function(x) SetEdgeStyle(x, color = "red", inherit = FALSE),
filterFun =
function(x) !x$isRoot && x$parent$type == "decision" && x$parent$decision == x$name)Finalmente, se define el estilo de representación de izquierda a derecha, y se usa la función “plot()” para ello:
SetGraphStyle(jl, rankdir = "LR")
plot(jl)