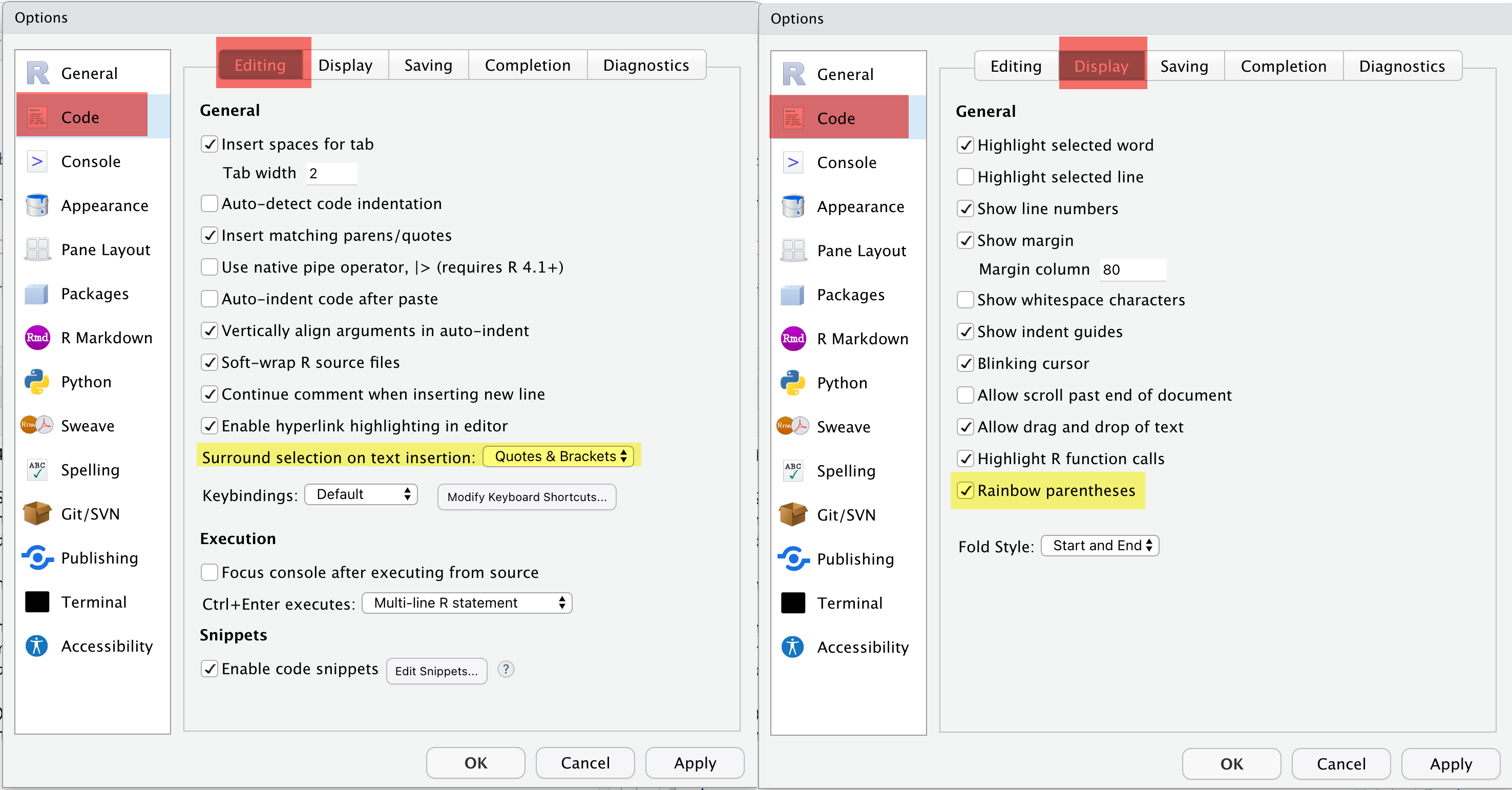
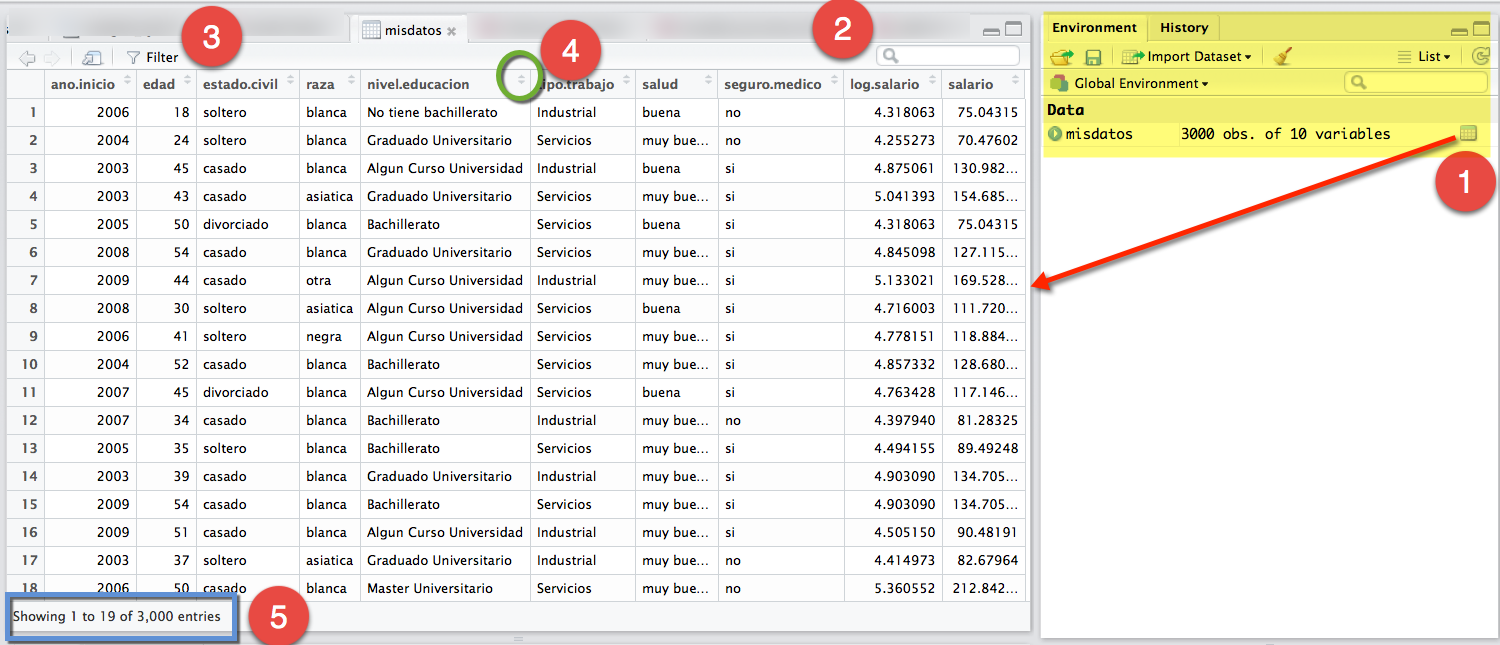
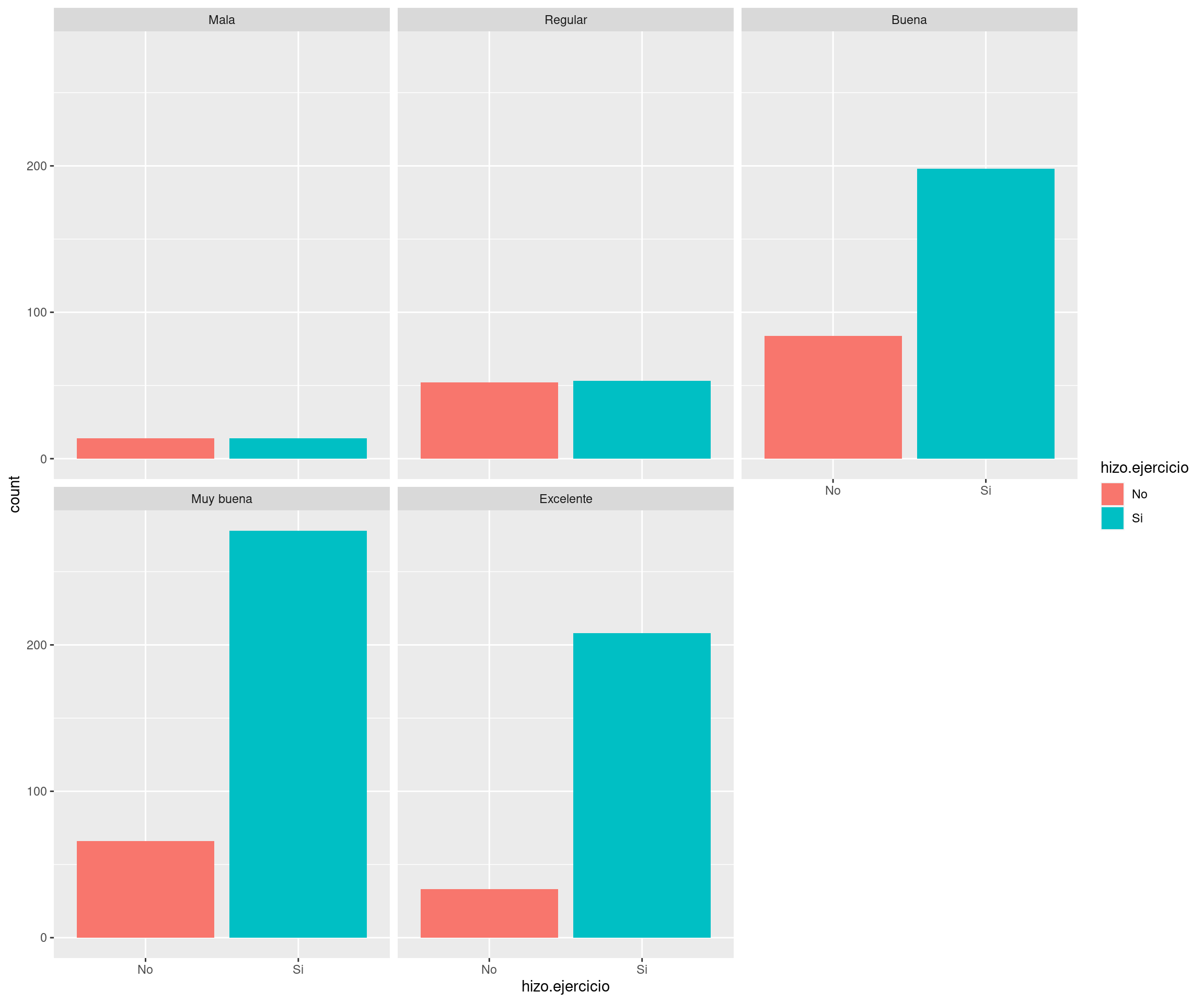
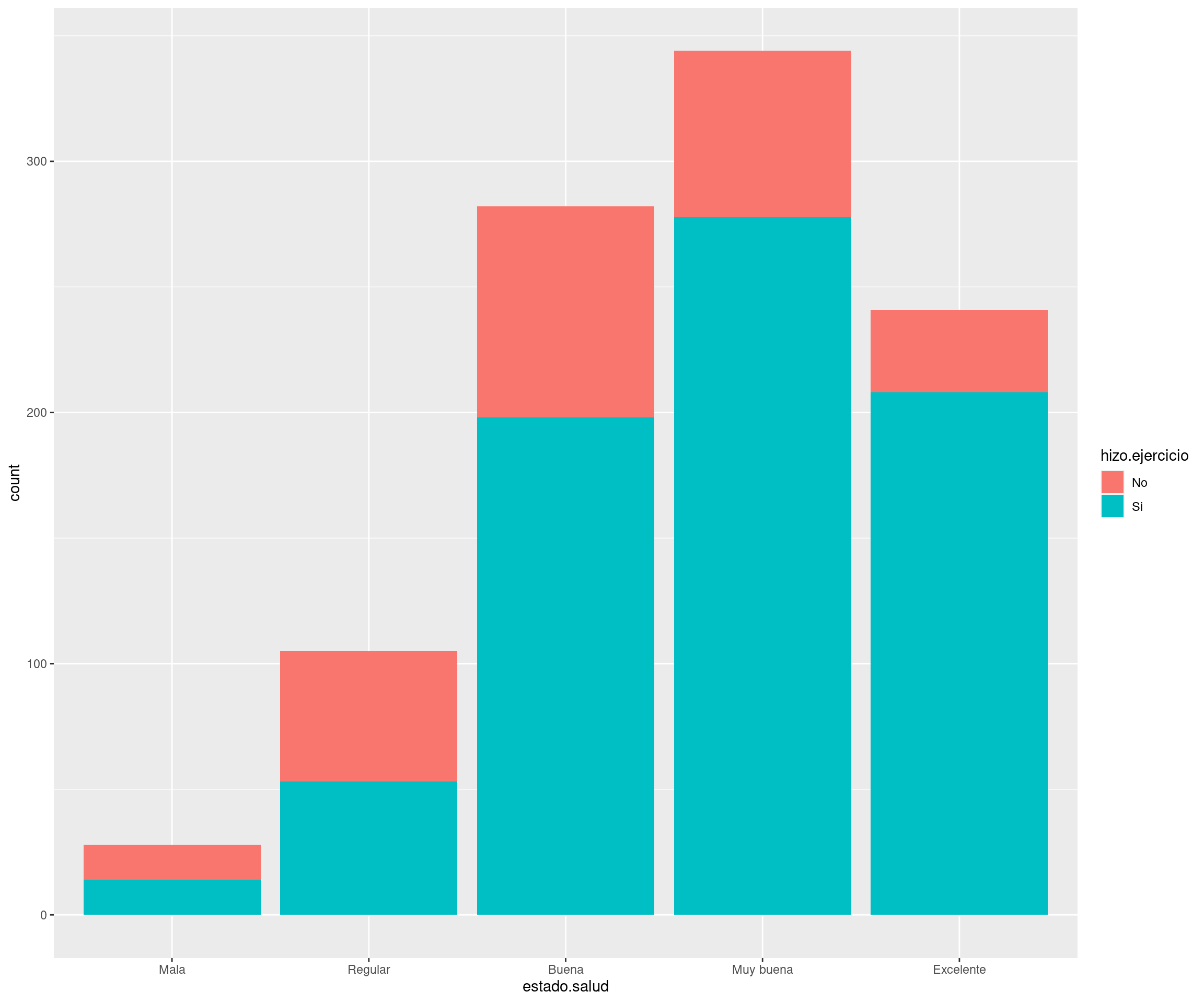
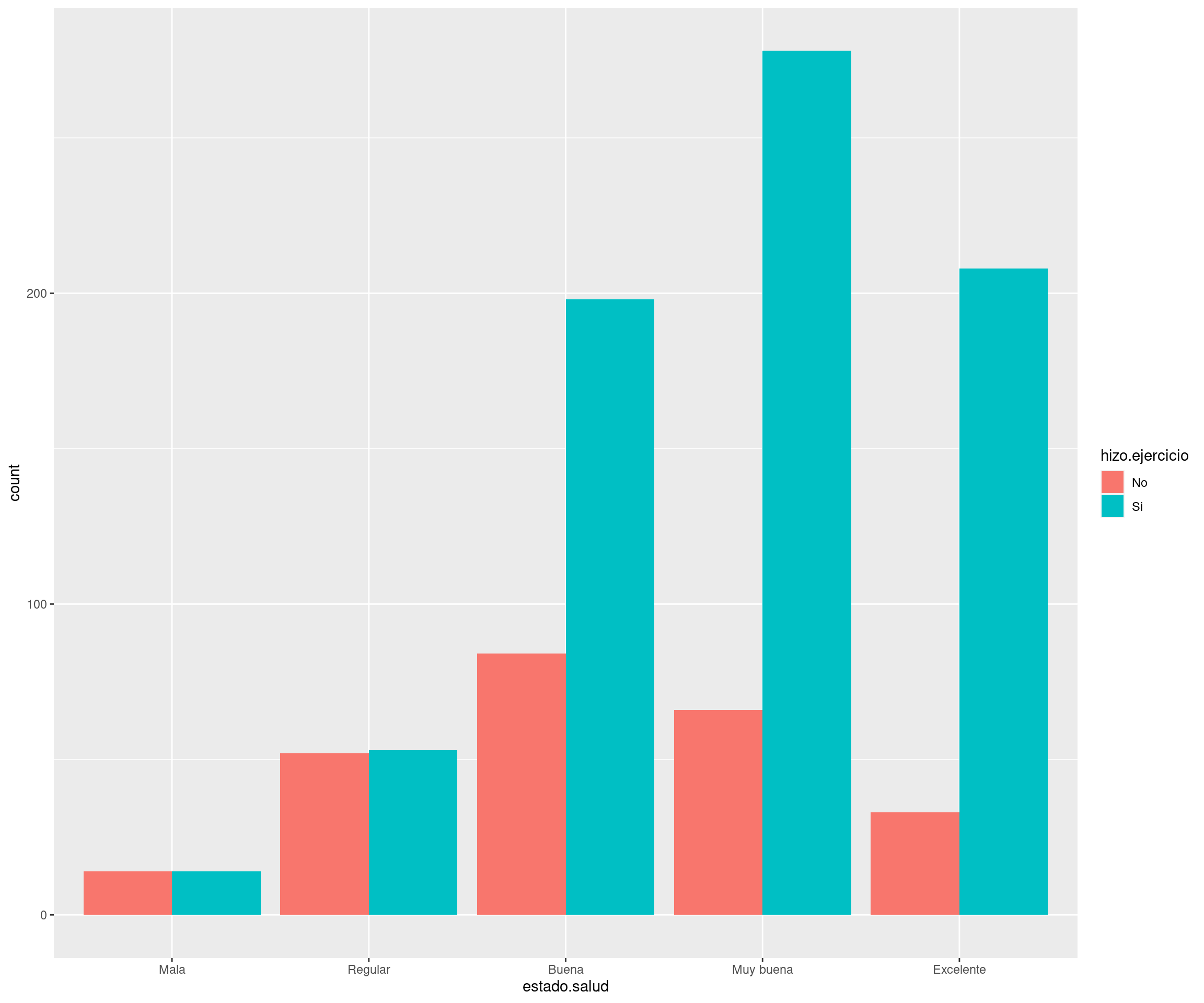
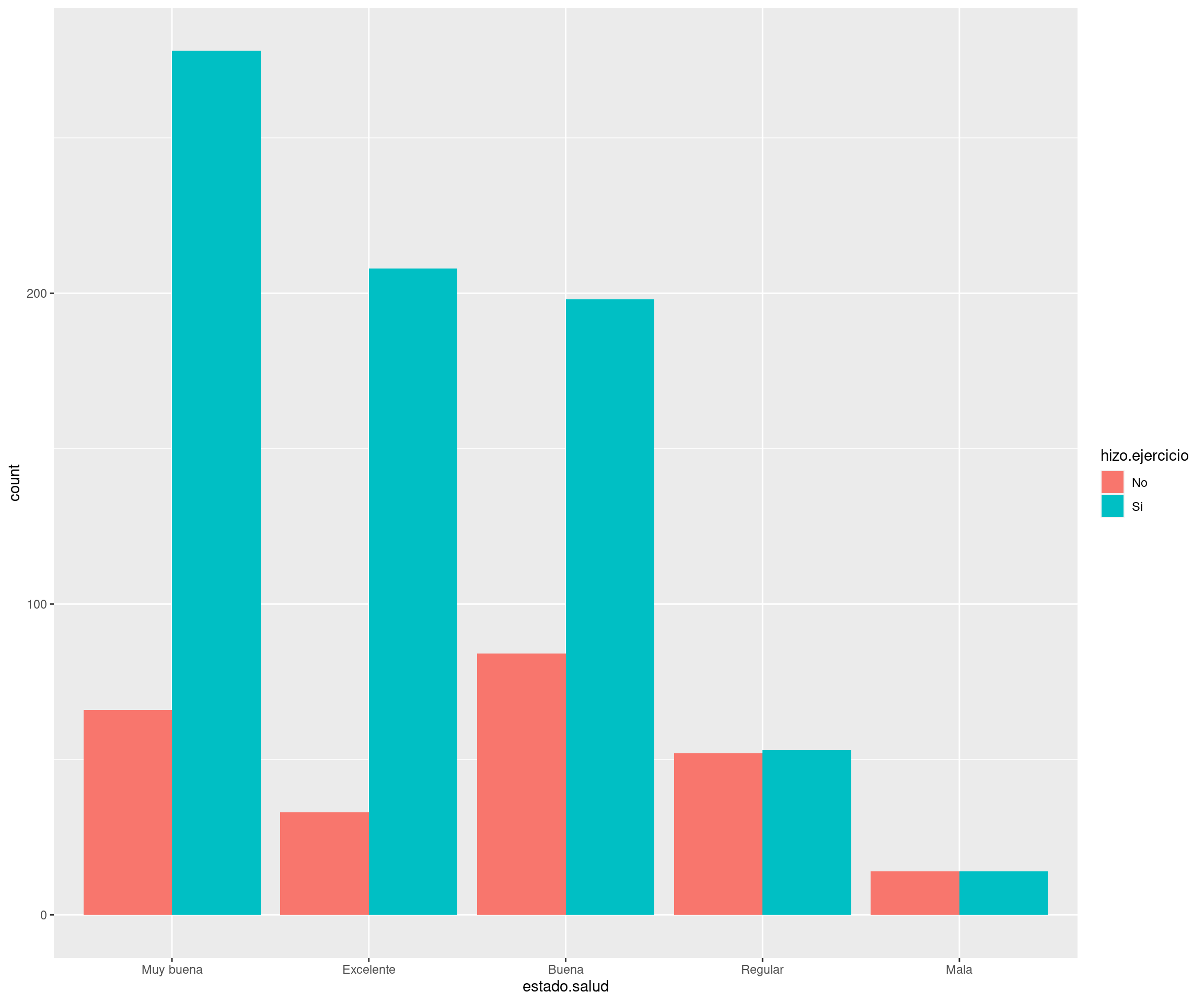
Introducción a R
En esta página se hace una introducción al lenguaje R para su uso en Estadística básica
R básico
1 Introducción
Se recomienda visitar el siguiente enlace para instalar R, RStudio y LaTeX en su ordenador personal:
-
Vídeos sobre cuestiones básicas de R y RStudio:
-
Referencias interesantes para aprender más sobre: R, RStudio, Quarto, R Markdown, etc.
-
Libros interesantes gratuitos:
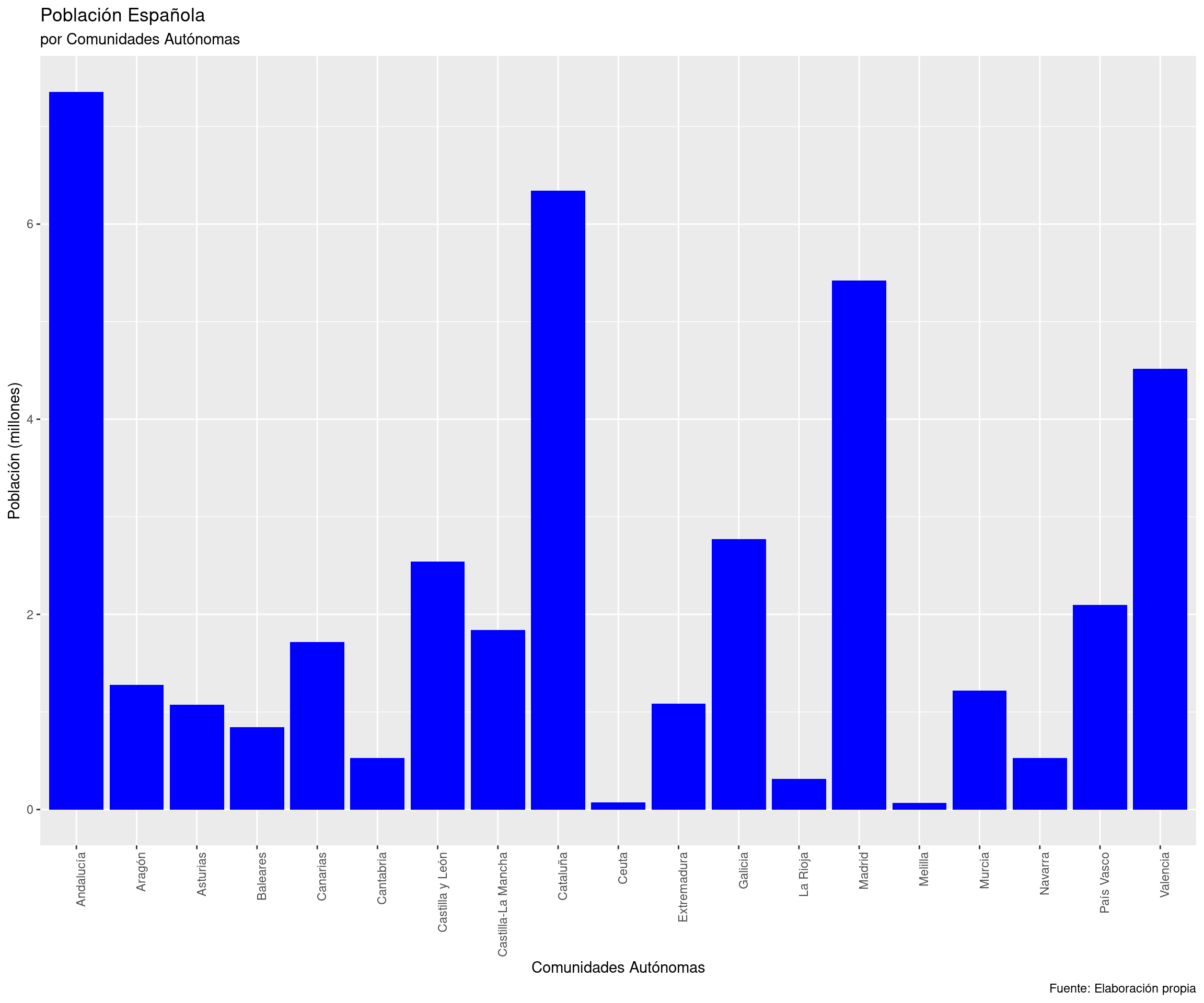
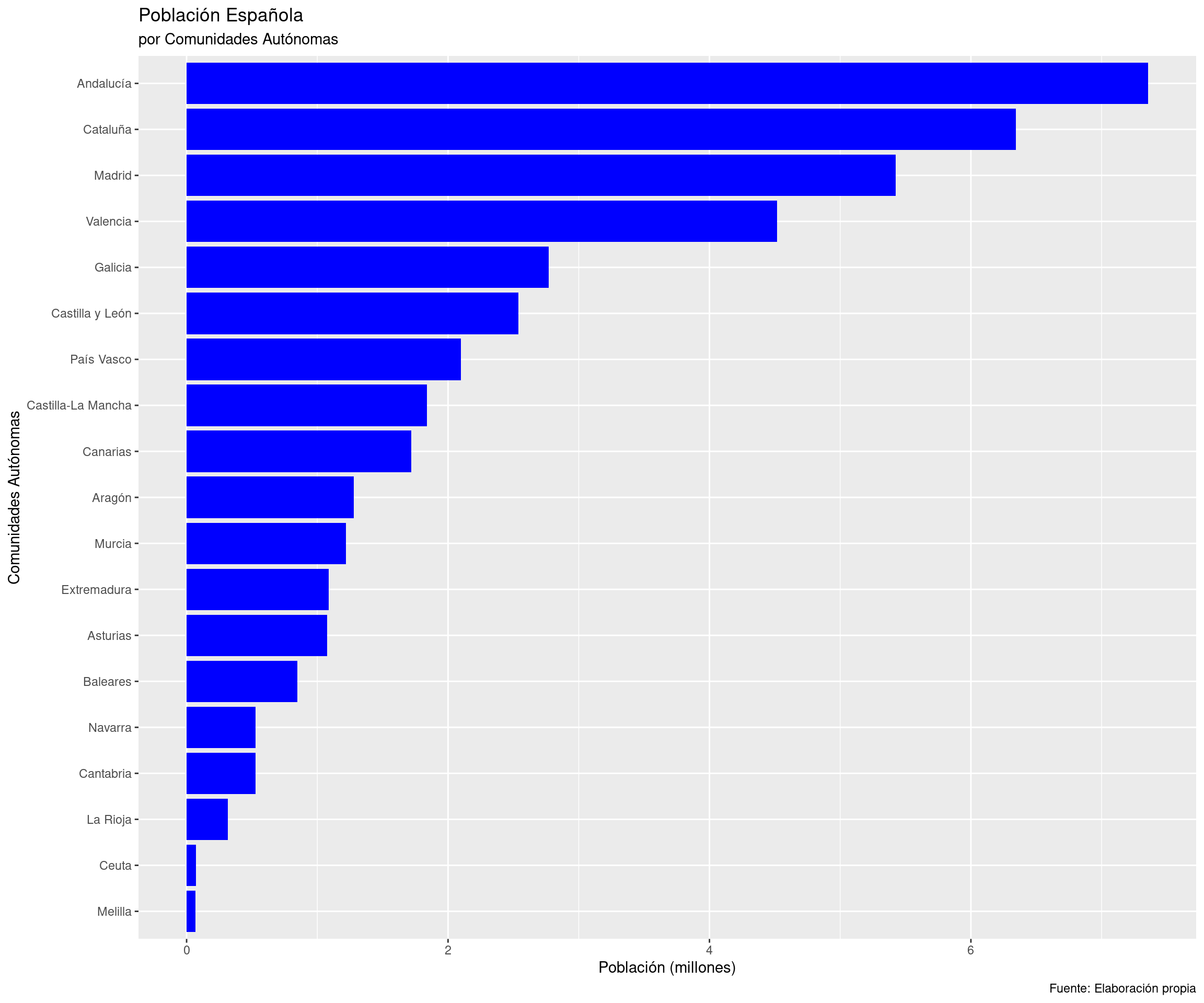
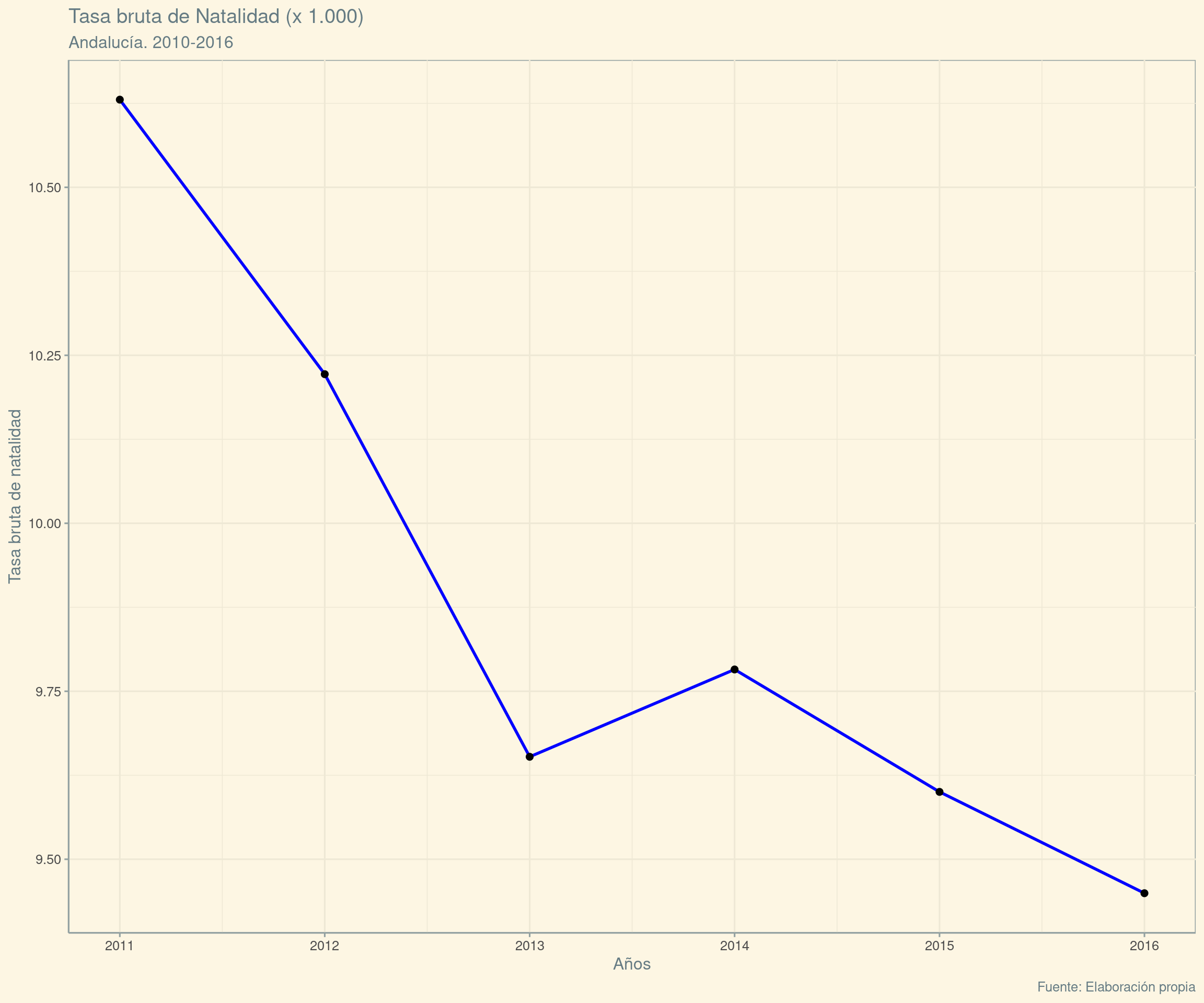
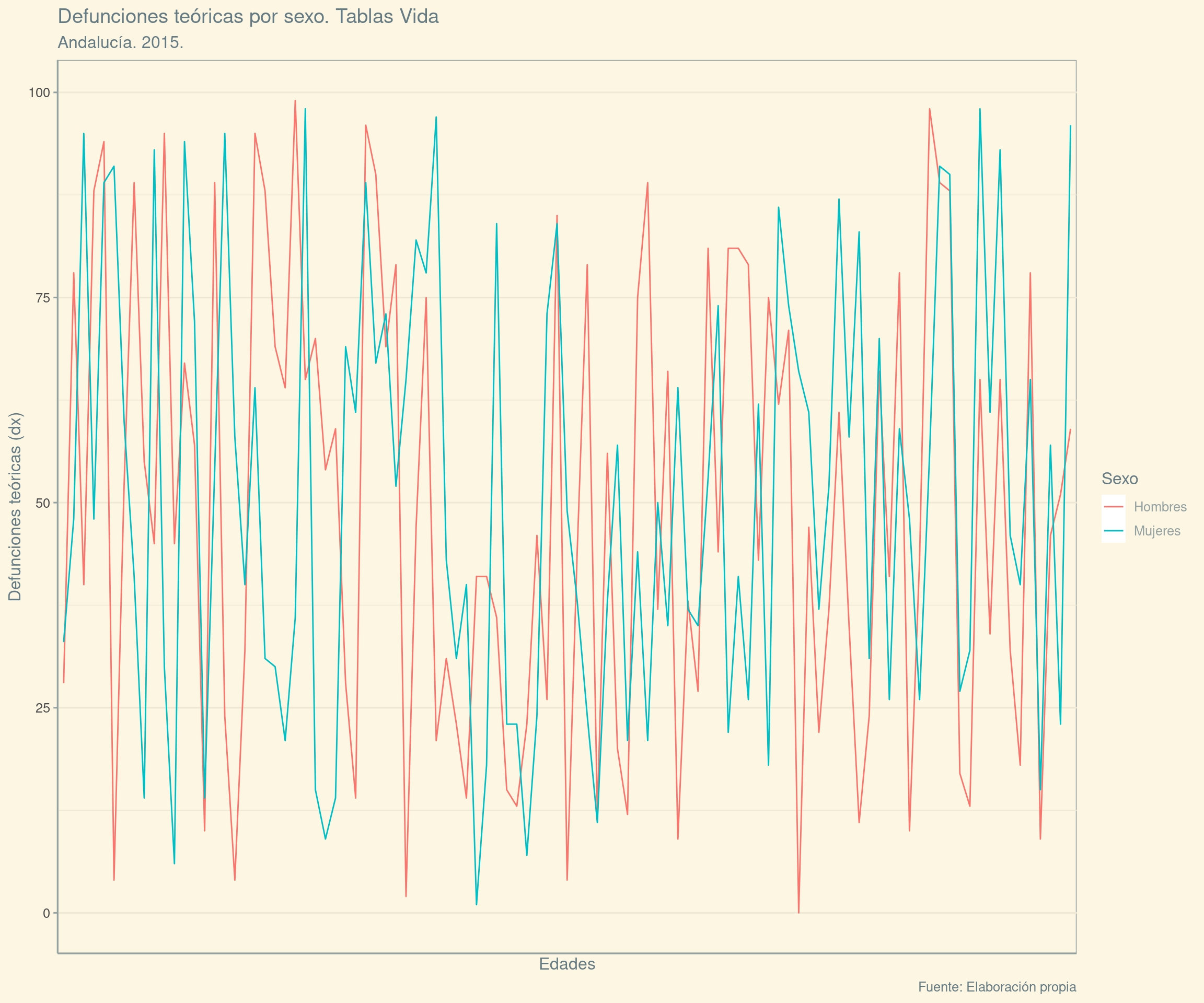
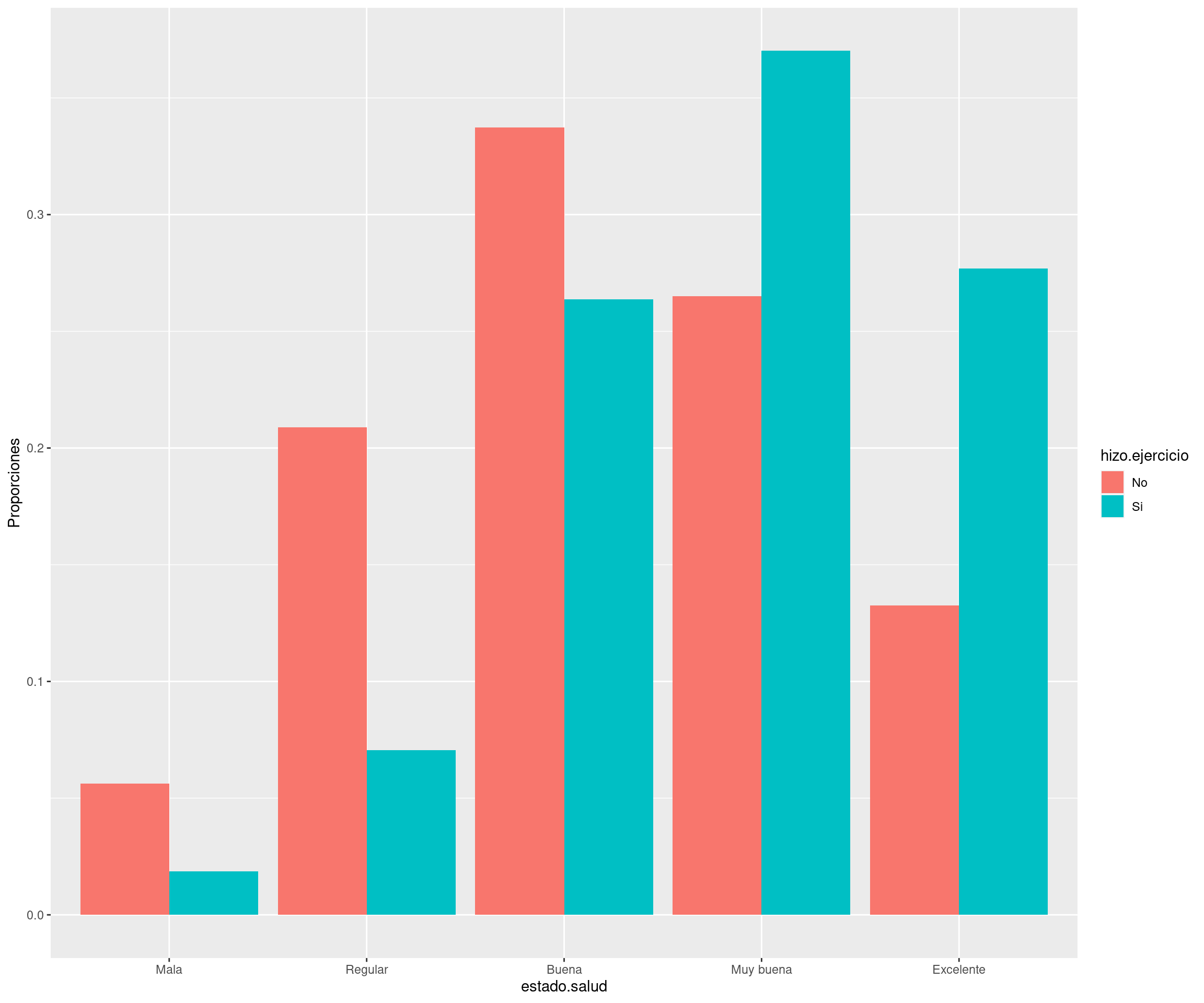
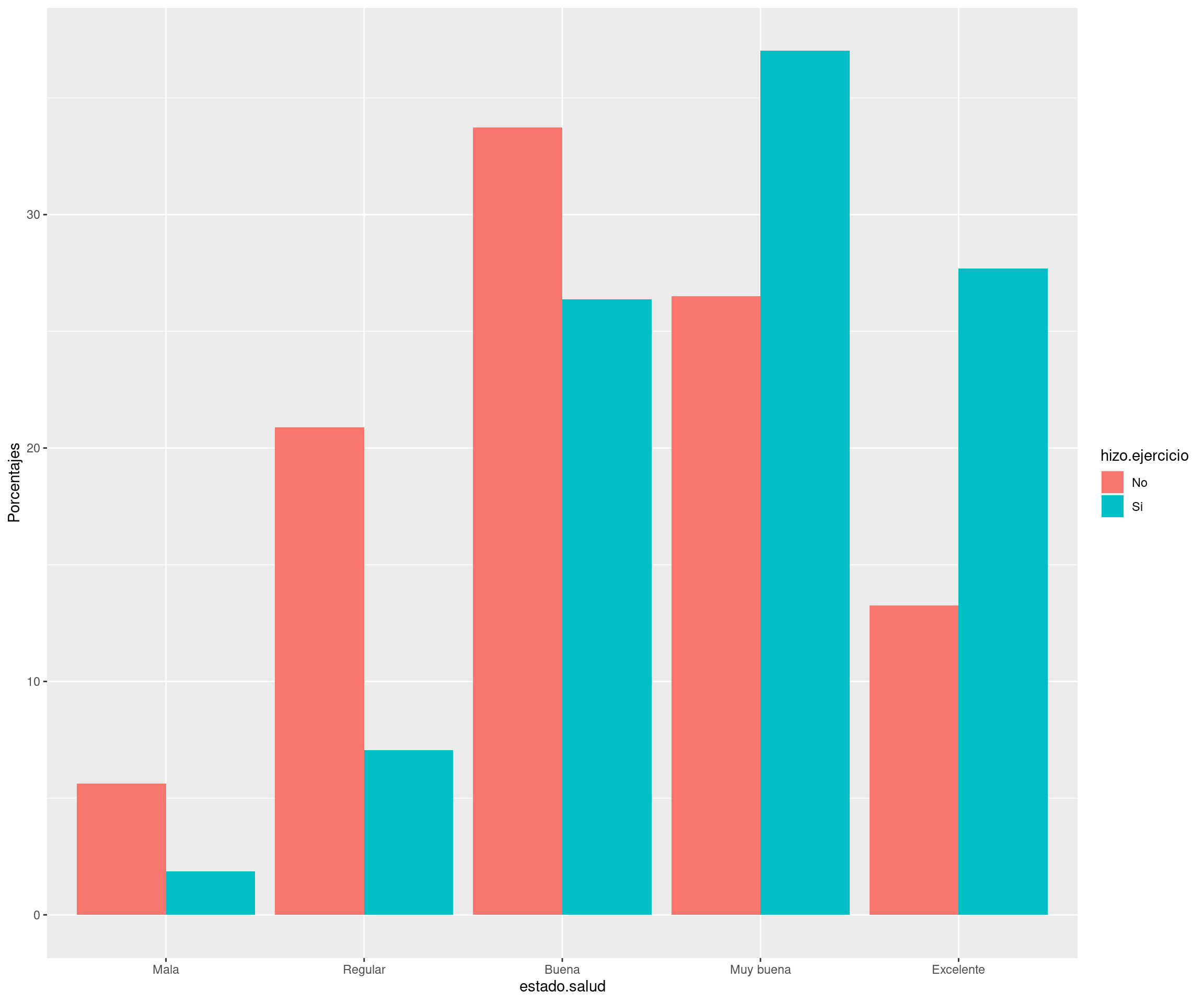
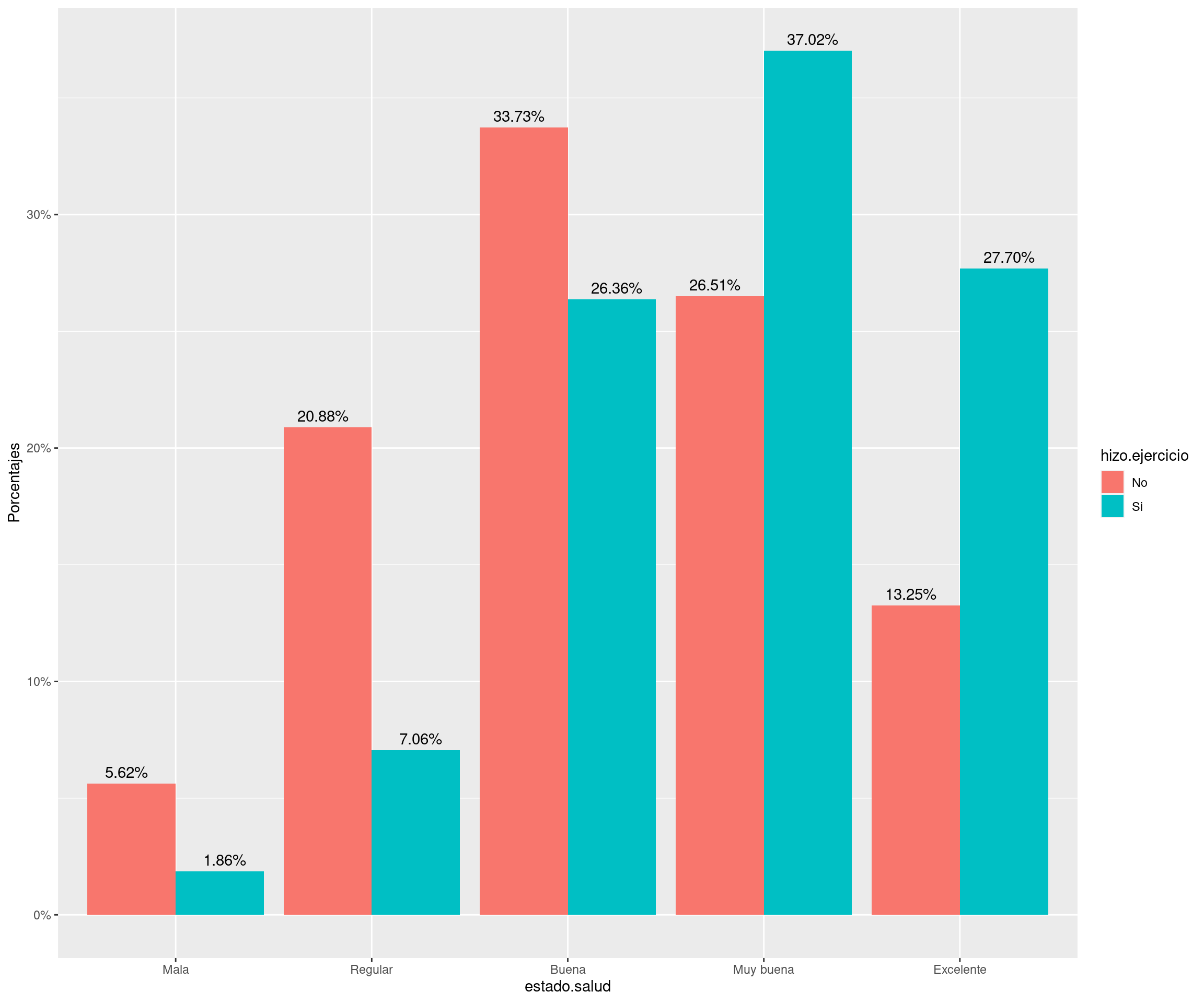
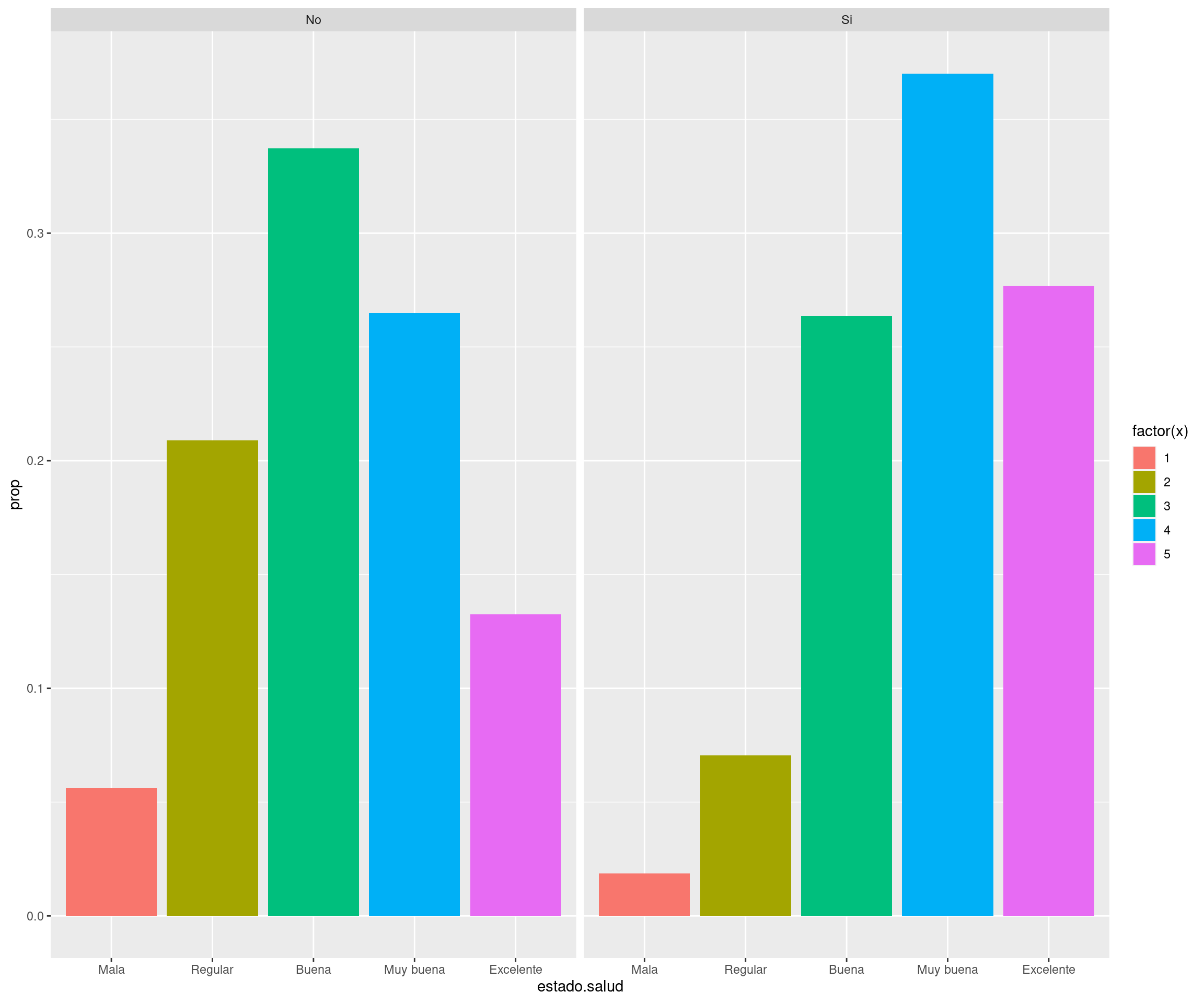
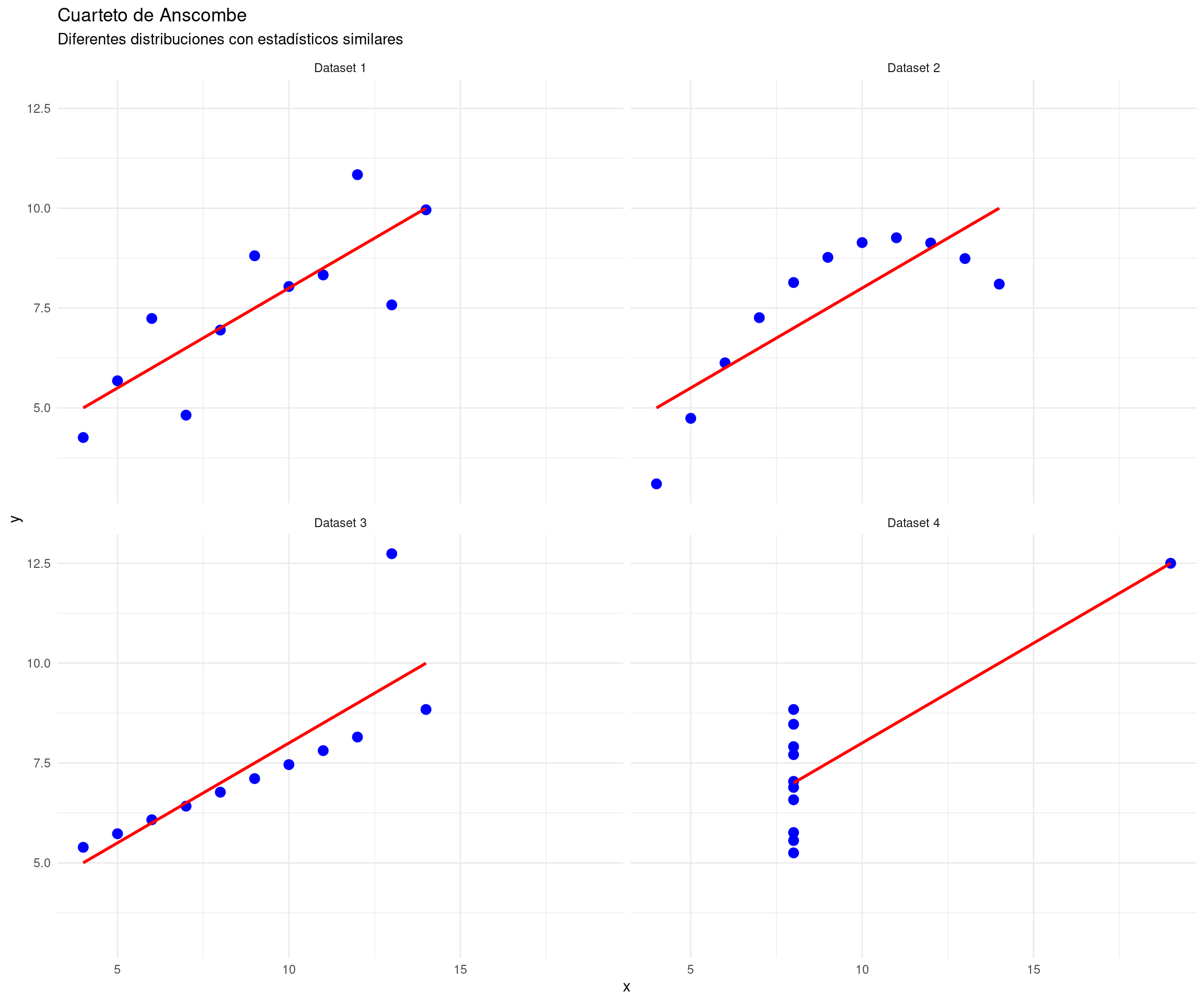
2 Galería de imágenes sobre R, RStudio, …
3 Ejemplo introductorio
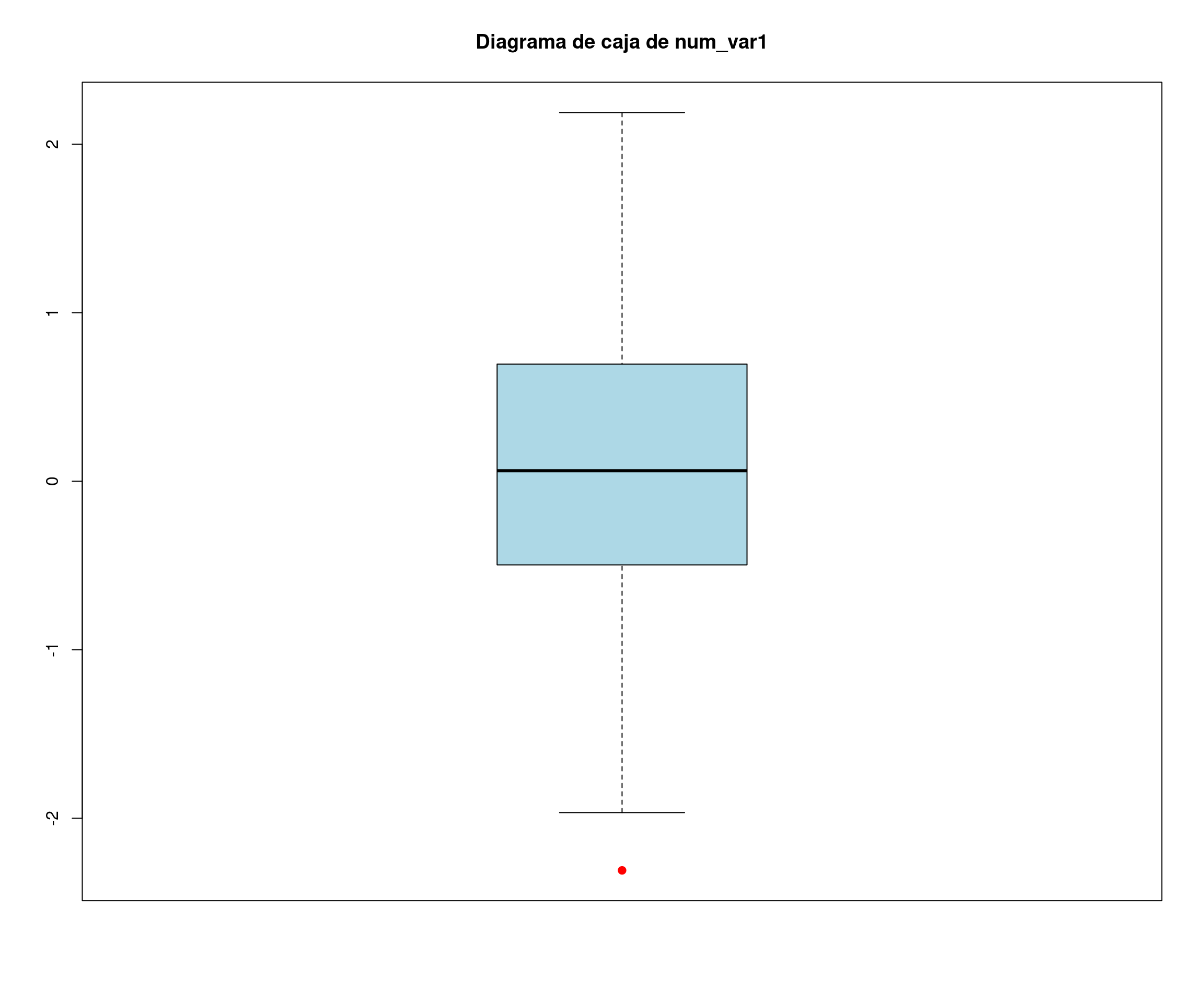
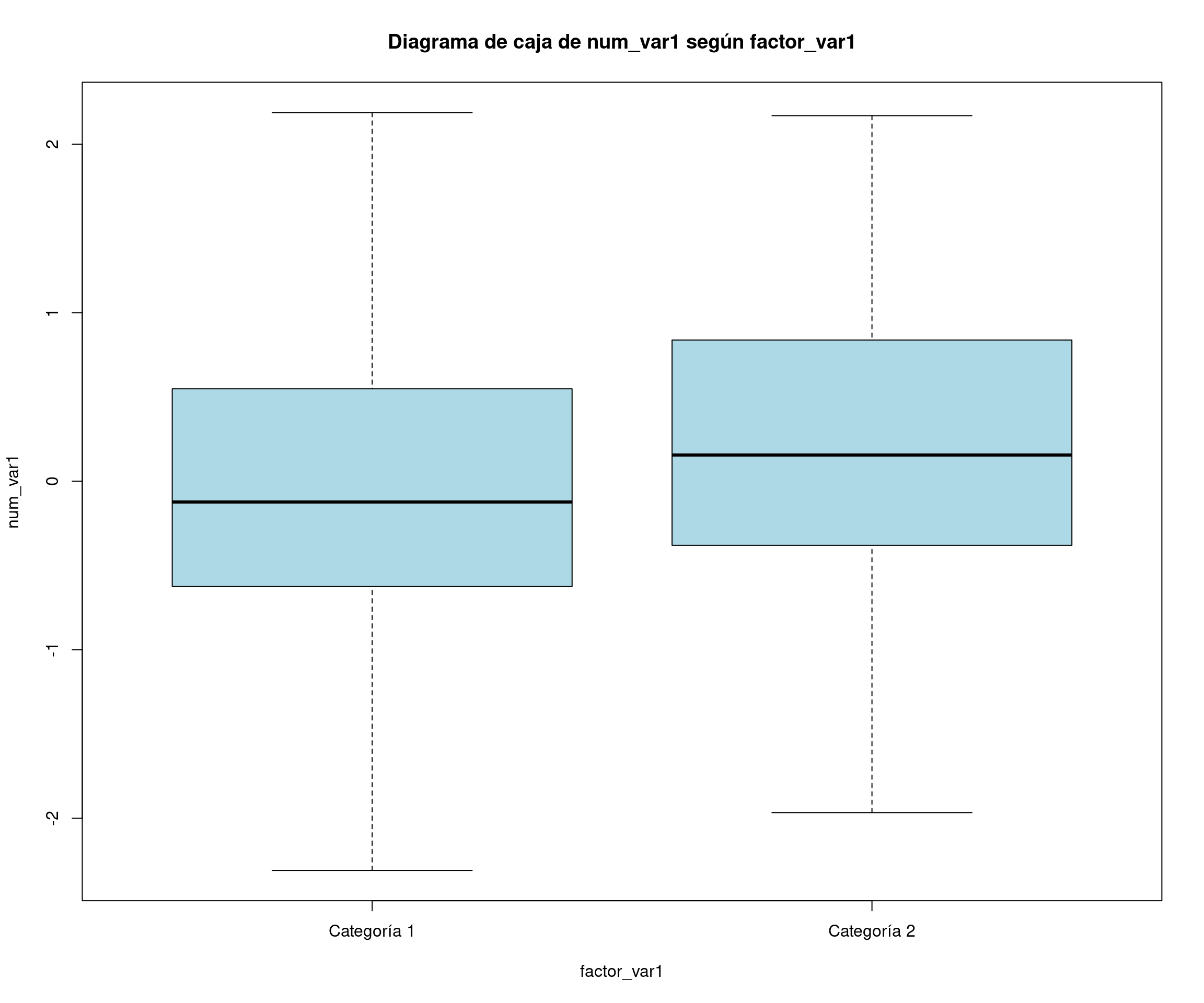
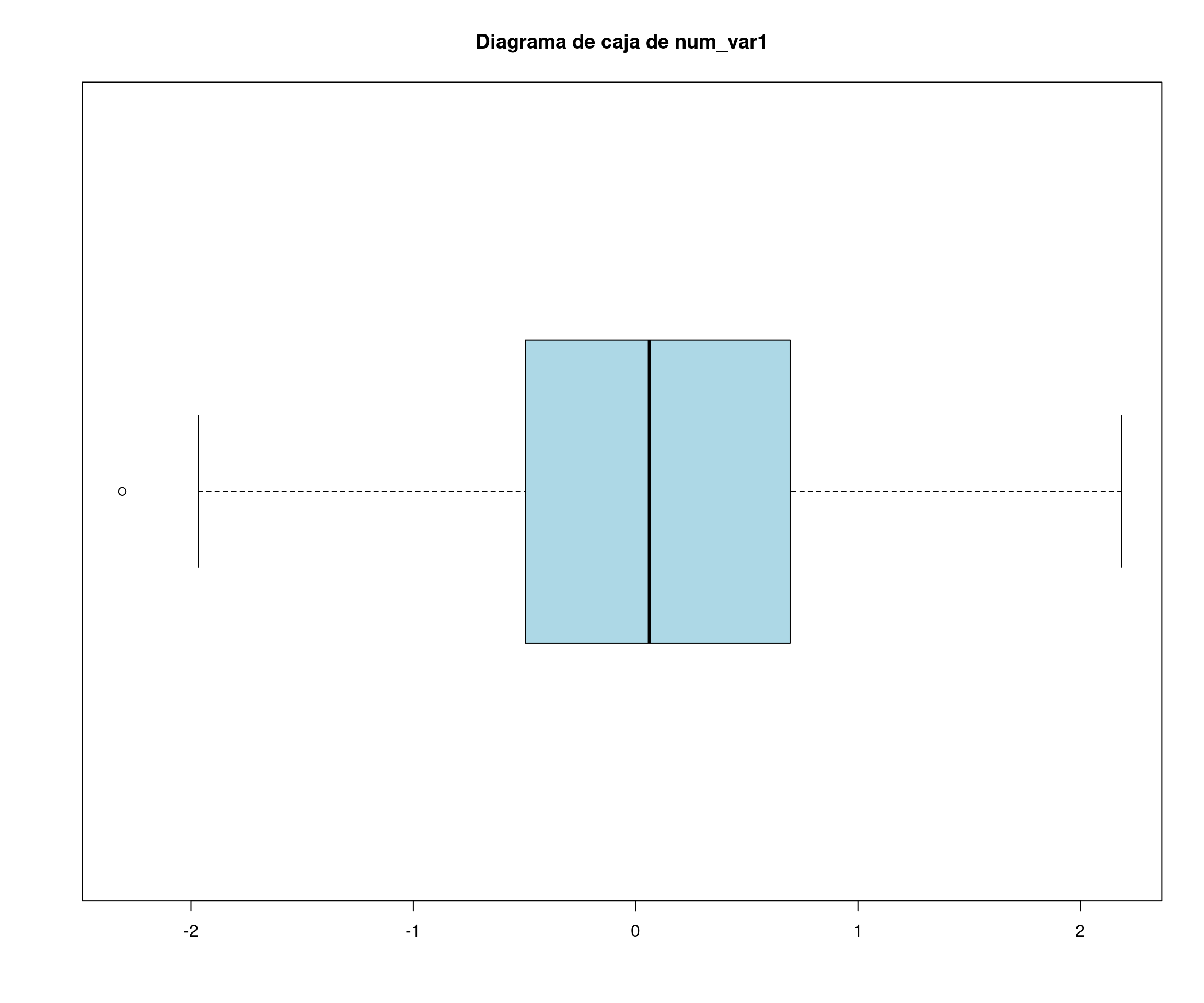
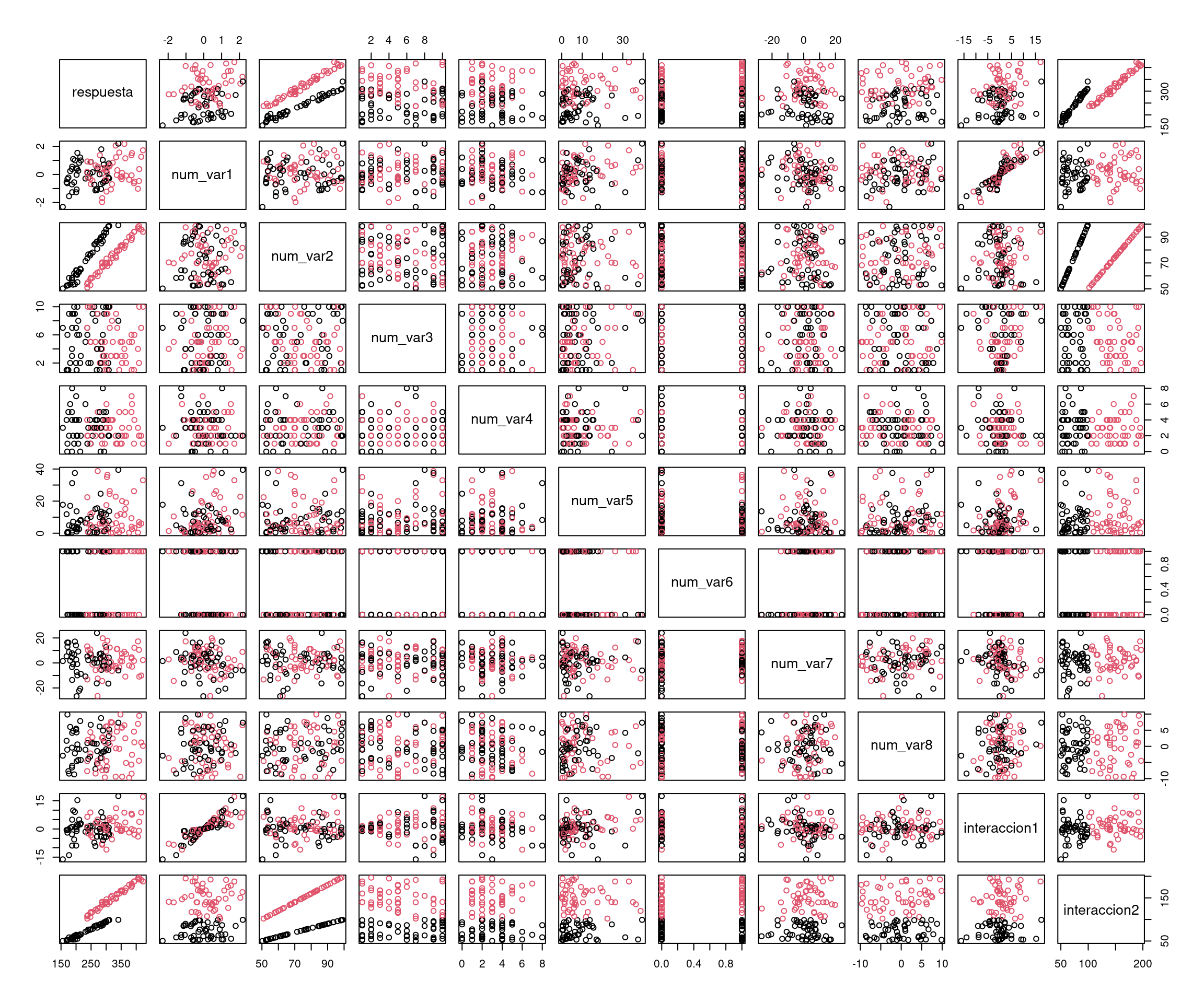
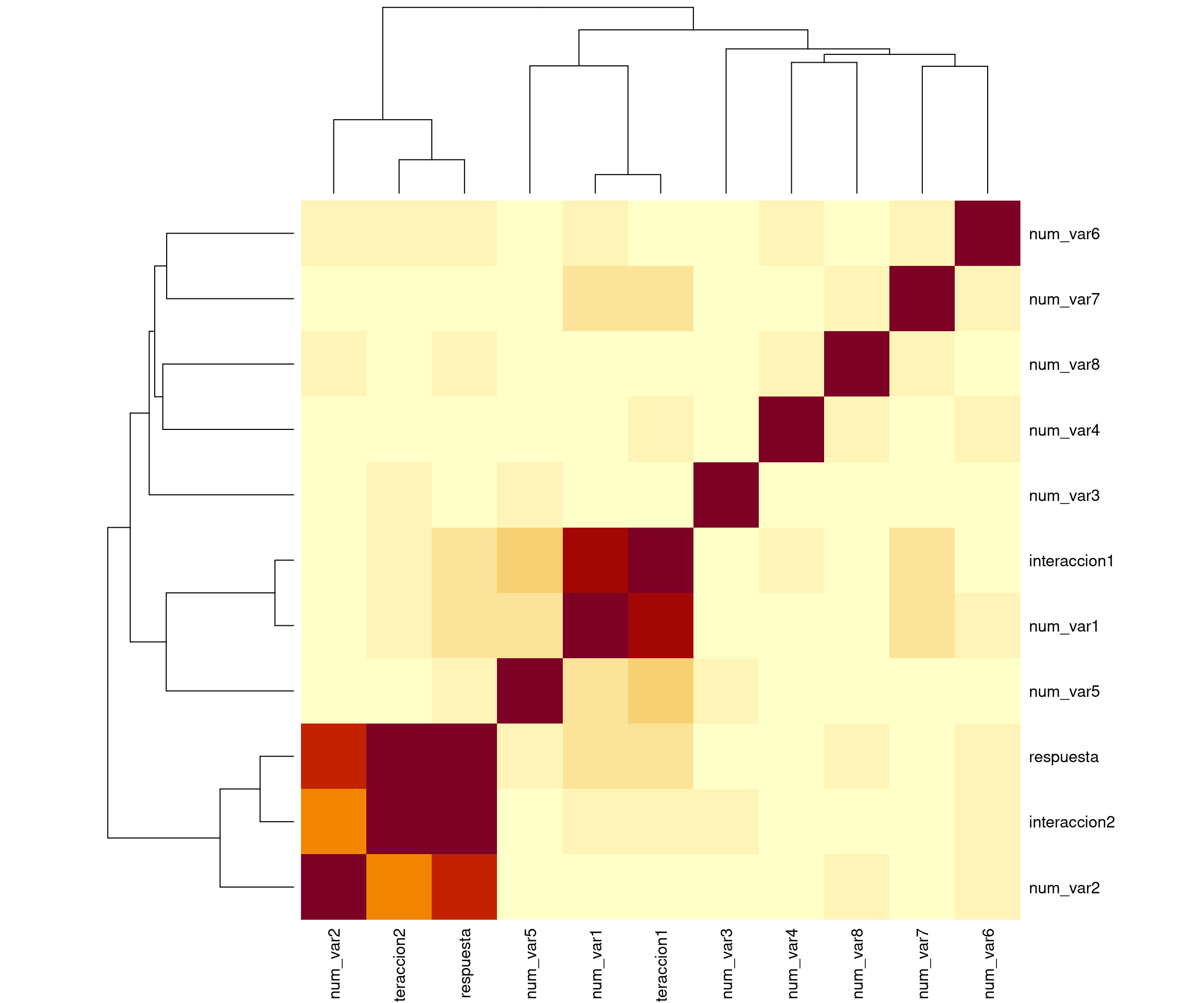
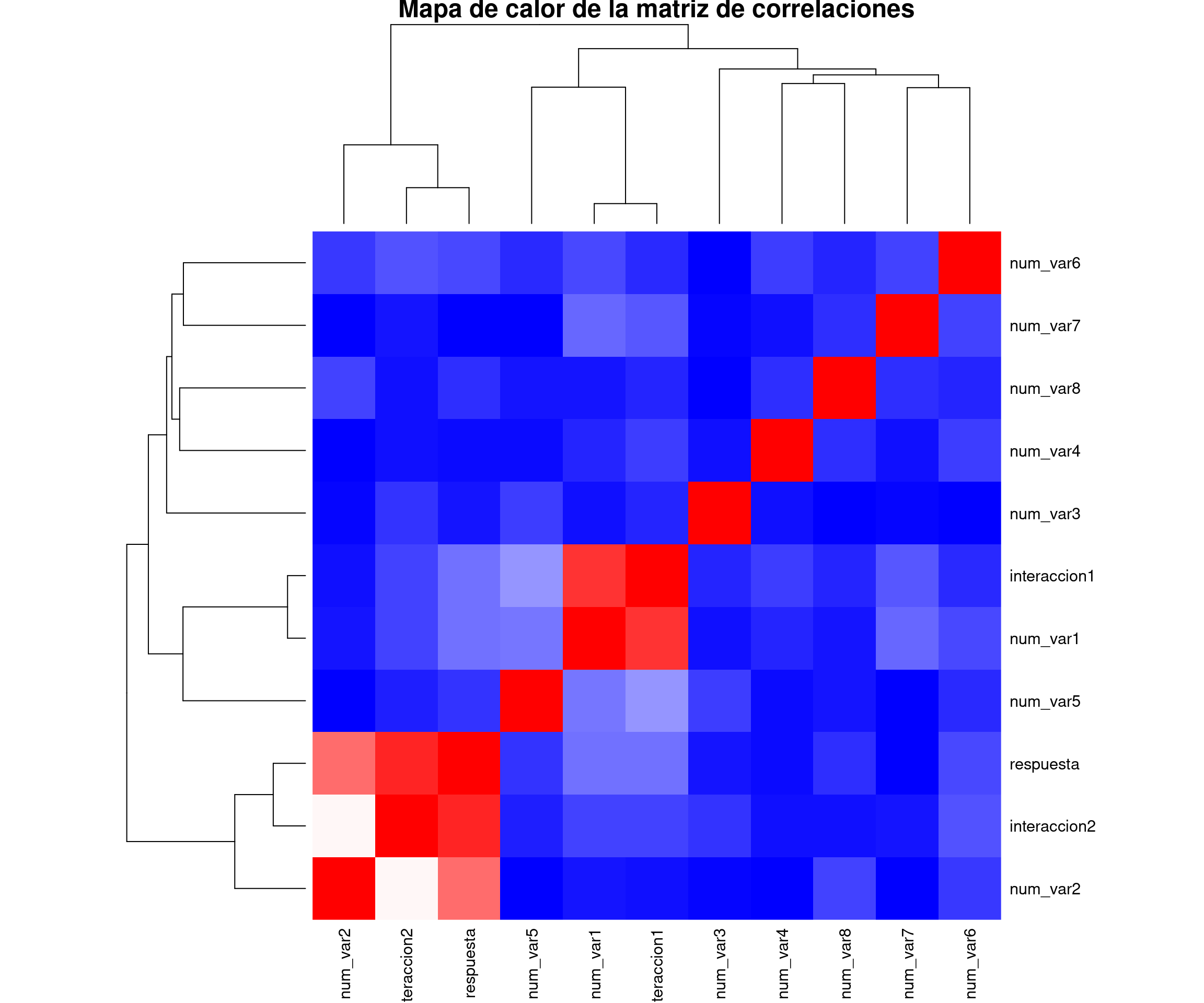
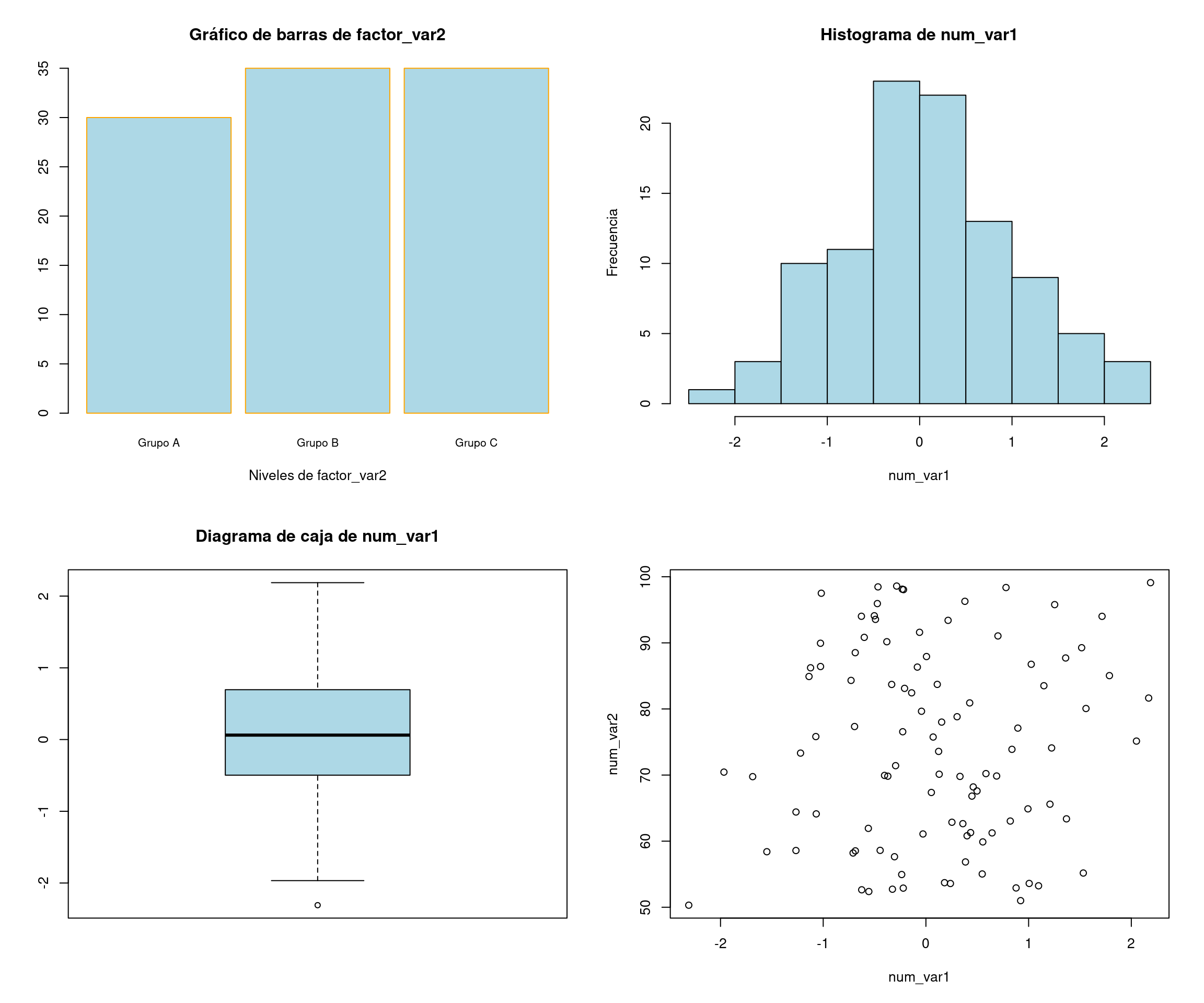
En este ejemplo se muestra cómo generar un conjunto de datos de ejemplo para un problema de regresión. Se generan variables numéricas y categóricas significativas y no significativas, y se crea una variable de respuesta como una combinación lineal de las predictoras.
# Establecer la semilla para reproductibilidad
set.seed(123)
# número de valores a generar
nsim <- 100
# Generar variables numéricas significativas
num_var1 <- rnorm(nsim) # Variable numérica normal
num_var2 <- runif(nsim, min = 50, max = 100) # Variable numérica uniforme
num_var3 <- sample(1:10, nsim, replace = TRUE) # Variable numérica entera
num_var4 <- rpois(nsim, lambda = 3) # Variable numérica de Poisson
num_var5 <- rexp(nsim, rate = 0.1) # Variable numérica exponencial
num_var6 <- rbinom(nsim, size = 1, prob = 0.5) # Variable numérica binomial
# Generar variables numéricas poco significativas
num_var7 <- rnorm(nsim, mean = 0, sd = 10) # Variable numérica con alta varianza
num_var8 <- runif(nsim, min = -10, max = 10) # Variable numérica con rango amplio
# Generar variables de factor significativas
factor_var1 <- factor(sample(c("Categoría 1", "Categoría 2"), nsim, replace = TRUE))
factor_var2 <- factor(sample(c("Grupo A", "Grupo B", "Grupo C"), nsim, replace = TRUE))
# Generar variables de factor poco significativas
factor_var3 <- factor(sample(c("Nivel 1", "Nivel 2"), nsim, replace = TRUE))
factor_var4 <- factor(sample(c("Tipo X", "Tipo Y", "Tipo Z", "Tipo W"), nsim, replace = TRUE))
# Crear interacciones entre variables
interaccion1 <- num_var1 * num_var3
interaccion2 <- num_var2 * as.numeric(factor_var1)
# Generar la variable de respuesta con una combinación lineal de las predictoras e interacciones
respuesta <- 5 + 1.5 * num_var1 + 2 * num_var2 + 0.5 * num_var3 +
0.3 * num_var4 + 0.2 * num_var5 +
3 * as.numeric(factor_var1) + 2 * as.numeric(factor_var2) +
interaccion1 + interaccion2 + rnorm(nsim)
# Crear el data.frame
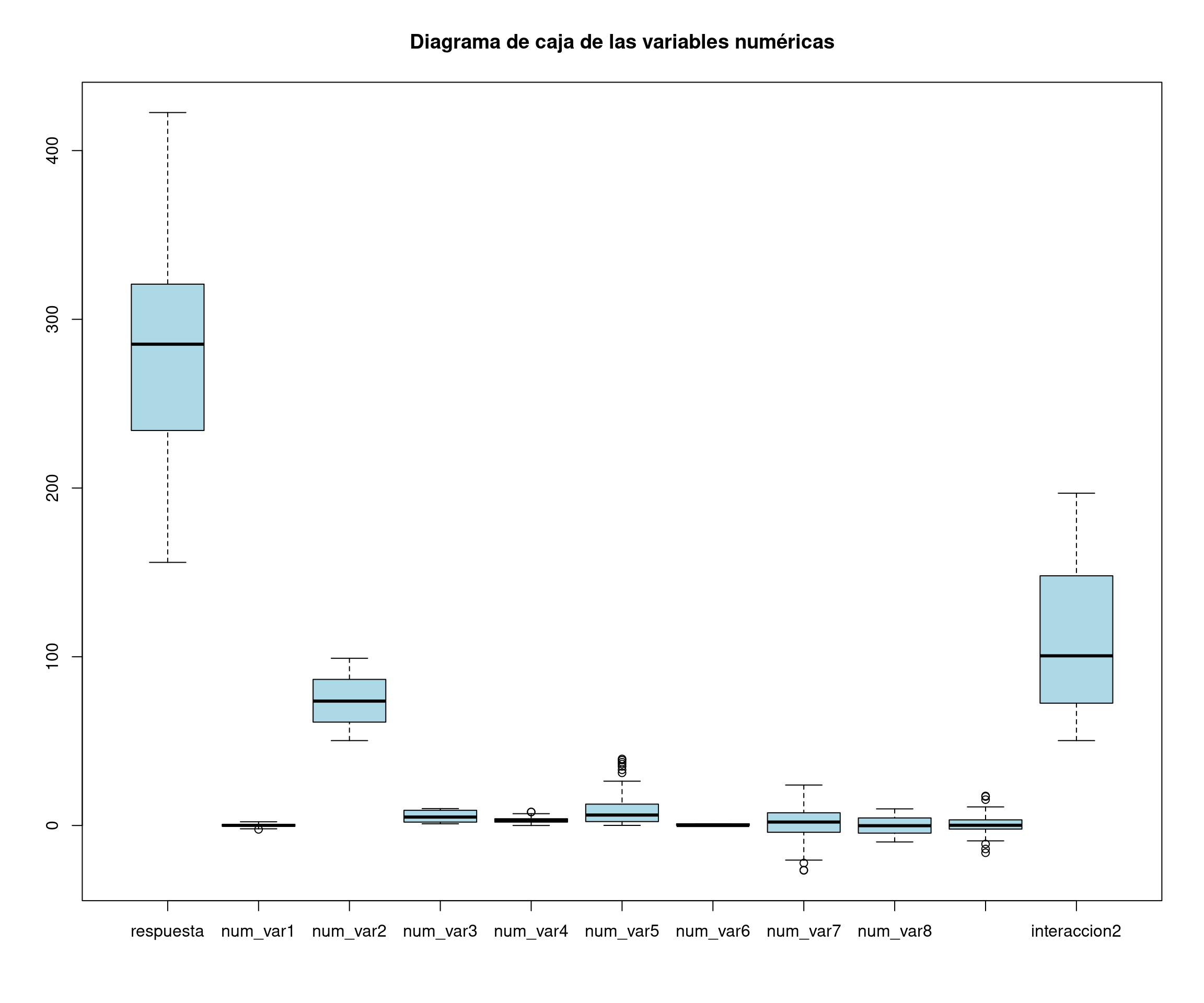
datos <- data.frame(respuesta, num_var1, num_var2, num_var3, num_var4, num_var5, num_var6,
num_var7, num_var8, factor_var1, factor_var2, factor_var3, factor_var4,
interaccion1, interaccion2)
# Ver las primeras filas del data.frame
head(datos, 10) respuesta num_var1 num_var2 num_var3 num_var4 num_var5 num_var6 num_var7 num_var8 factor_var1 factor_var2
1 193.7298 -0.56047565 61.93630 10 1 3.6716983 0 6.706960 -8.6874378 Categoría 1 Grupo A
2 307.5329 -0.23017749 98.11795 10 2 3.3147029 0 -16.505465 -1.1893375 Categoría 1 Grupo A
3 343.7469 1.55870831 80.06829 1 5 0.5978492 1 -3.497542 -0.7580228 Categoría 2 Grupo C
4 246.6869 0.07050839 75.75149 10 4 0.1968580 1 7.564064 -3.1813126 Categoría 1 Grupo C
5 302.8175 0.12928774 70.12867 1 4 35.0000668 1 -5.388092 -6.2971936 Categoría 2 Grupo A
6 422.5490 1.71506499 94.01233 10 1 32.9930824 1 2.272919 0.1399545 Categoría 2 Grupo A
7 295.8890 0.46091621 68.20459 5 1 1.3937846 0 4.922286 -9.6161794 Categoría 2 Grupo C
8 200.4055 -1.26506123 64.41196 7 7 3.0052300 0 2.678350 5.4737208 Categoría 1 Grupo B
9 249.1545 -0.68685285 58.53226 5 3 3.0753336 0 6.532577 1.1933016 Categoría 2 Grupo B
10 254.4785 -0.44566197 58.60859 10 3 12.7416223 0 -1.227087 2.8292528 Categoría 2 Grupo C
factor_var3 factor_var4 interaccion1 interaccion2
1 Nivel 2 Tipo Z -5.6047565 61.93630
2 Nivel 1 Tipo Z -2.3017749 98.11795
3 Nivel 1 Tipo Z 1.5587083 160.13657
4 Nivel 2 Tipo X 0.7050839 75.75149
5 Nivel 2 Tipo X 0.1292877 140.25733
6 Nivel 1 Tipo W 17.1506499 188.02465
7 Nivel 1 Tipo Z 2.3045810 136.40919
8 Nivel 1 Tipo Z -8.8554286 64.41196
9 Nivel 1 Tipo X -3.4342643 117.06452
10 Nivel 1 Tipo Z -4.4566197 117.21717| respuesta | num_var1 | num_var2 | num_var3 | num_var4 | num_var5 | num_var6 | num_var7 | num_var8 | factor_var1 | factor_var2 | factor_var3 | factor_var4 | interaccion1 | interaccion2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 193.7298 | -0.5604756 | 61.93630 | 10 | 1 | 3.6716983 | 0 | 6.706960 | -8.6874378 | Categoría 1 | Grupo A | Nivel 2 | Tipo Z | -5.6047565 | 61.93630 |
| 307.5329 | -0.2301775 | 98.11795 | 10 | 2 | 3.3147029 | 0 | -16.505465 | -1.1893375 | Categoría 1 | Grupo A | Nivel 1 | Tipo Z | -2.3017749 | 98.11795 |
| 343.7469 | 1.5587083 | 80.06829 | 1 | 5 | 0.5978492 | 1 | -3.497542 | -0.7580228 | Categoría 2 | Grupo C | Nivel 1 | Tipo Z | 1.5587083 | 160.13657 |
| 246.6869 | 0.0705084 | 75.75149 | 10 | 4 | 0.1968580 | 1 | 7.564064 | -3.1813126 | Categoría 1 | Grupo C | Nivel 2 | Tipo X | 0.7050839 | 75.75149 |
| 302.8175 | 0.1292877 | 70.12867 | 1 | 4 | 35.0000668 | 1 | -5.388092 | -6.2971936 | Categoría 2 | Grupo A | Nivel 2 | Tipo X | 0.1292877 | 140.25733 |
| 422.5490 | 1.7150650 | 94.01233 | 10 | 1 | 32.9930824 | 1 | 2.272919 | 0.1399545 | Categoría 2 | Grupo A | Nivel 1 | Tipo W | 17.1506499 | 188.02465 |
| 295.8890 | 0.4609162 | 68.20459 | 5 | 1 | 1.3937846 | 0 | 4.922286 | -9.6161794 | Categoría 2 | Grupo C | Nivel 1 | Tipo Z | 2.3045810 | 136.40919 |
| 200.4055 | -1.2650612 | 64.41196 | 7 | 7 | 3.0052300 | 0 | 2.678350 | 5.4737208 | Categoría 1 | Grupo B | Nivel 1 | Tipo Z | -8.8554286 | 64.41196 |
| 249.1545 | -0.6868529 | 58.53226 | 5 | 3 | 3.0753336 | 0 | 6.532577 | 1.1933016 | Categoría 2 | Grupo B | Nivel 1 | Tipo X | -3.4342643 | 117.06452 |
| 254.4785 | -0.4456620 | 58.60859 | 10 | 3 | 12.7416223 | 0 | -1.227087 | 2.8292528 | Categoría 2 | Grupo C | Nivel 1 | Tipo Z | -4.4566197 | 117.21717 |
4 Consola de R para practicar
Solo tienes que escribir el código en la consola y presionar Ctrl+Enter (Cmd+Enter en MacOS) o sobre el botón “Run Code” para ejecutarlo.
Accede a cualquiera de los siguientes enlaces para practicar con R:
5 Creación de variables o vectores en R para almacenar datos
5.1 Vectores numéricos
Para analizar la longitud de unos dispositivos electrónicos fabricados por un proceso A, se extrajo una muestra aleatoria de seis dispositivos, obteniéndose los siguientes resultados:
1.8, 1.2, 1.6, 1.7, 1.1, 1.0
Se pueden guardar estos datos en un vector o variable proceso_A (ver: Sección 13.1) de la siguiente manera (separando cada valor por una coma y los números decimales se escriben y utilizando el “.” como signo decimal siempre en R):
proceso_A = c(1.8, 1.2, 1.6, 1.7, 1.1, 1.0)
proceso_A[1] 1.8 1.2 1.6 1.7 1.1 1.0Para crear un vector con una secuencia de números, se puede usar el operador ::
secuencia = 1:10
secuencia [1] 1 2 3 4 5 6 7 8 9 10secuencia2 = 10:1
secuencia2 [1] 10 9 8 7 6 5 4 3 2 1secuencia3 = 1.5:10.5
secuencia3 [1] 1.5 2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5 10.5secuencia4 = 1:10.5
secuencia4 [1] 1 2 3 4 5 6 7 8 9 10Para crear un vector con una secuencia de números, se puede usar la función seq():
secuencia = seq(from = 1, to = 10, by = 2) # idem: seq(1,10,2)
secuencia[1] 1 3 5 7 9secuencia2 = seq(1, 10, length.out = 5)
secuencia2[1] 1.00 3.25 5.50 7.75 10.00(secuencia3a = seq(1, 10, by = 1)) [1] 1 2 3 4 5 6 7 8 9 10(secuencia3b = 1:10) [1] 1 2 3 4 5 6 7 8 9 10proceso_A[1] 1.8 1.2 1.6 1.7 1.1 1.0secuencia4 = seq(1, 10, along.with = proceso_A)
secuencia4[1] 1.0 2.8 4.6 6.4 8.2 10.0Para repetir un valor o una secuencia de valores, se puede usar la función rep():
repeticion = rep(1:3, times = 2)
repeticion[1] 1 2 3 1 2 3repeticion2 = rep(1:3, each = 2)
repeticion2[1] 1 1 2 2 3 3repeticion3 = rep(1:3, length.out = 10)
repeticion3 [1] 1 2 3 1 2 3 1 2 3 1repeticion4 = rep(1:3, times = 2, each = 3)
repeticion4 [1] 1 1 1 2 2 2 3 3 3 1 1 1 2 2 2 3 3 3repeticion5 = rep(1:3, length.out = 10, each = 2)
repeticion5 [1] 1 1 2 2 3 3 1 1 2 2repeticion5 = rep(1:3, times = 2, each = 3, length.out = 10)
repeticion5 [1] 1 1 1 2 2 2 3 3 3 15.1.1 Vectores de tipo “integer”
Los valores enteros o “integer” se pueden representar en R con la letra “L” al final del número entero: 1L, 2L, 3L, …
Los vectores de tipo “integer” se pueden crear con:
5.2 Vectores de caracteres
En este caso, los elementos del vector se escriben entre comillas dobles (
"...") o simples ('...').La creación de vectores se puede realizar casi del mismo modo que los vectores numéricos.
[1] "Juan" "María" "Pedro" "Ana" nombres[1] "Juan" "María" "Pedro" "Ana" # vector de caracteres con 2 elementos
# un elemento podría contener texto de más de un párrafo
textos1 = c(
"El análisis de datos puede ser divertido y desafiante a la vez
sobre todos si se usan herramientas como R y datos reales con muchos secretos por descubrir",
"El lenguaje R es muy versátil y se puede usar en diferentes áreas del conocimiento"
)
textos1[1] "El análisis de datos puede ser divertido y desafiante a la vez \n sobre todos si se usan herramientas como R y datos reales con muchos secretos por descubrir"
[2] "El lenguaje R es muy versátil y se puede usar en diferentes áreas del conocimiento" print(textos1)[1] "El análisis de datos puede ser divertido y desafiante a la vez \n sobre todos si se usan herramientas como R y datos reales con muchos secretos por descubrir"
[2] "El lenguaje R es muy versátil y se puede usar en diferentes áreas del conocimiento" cat(textos1) # cat(): interpreta los signos de \n (salto de línea), \t (tabulador), ...El análisis de datos puede ser divertido y desafiante a la vez
sobre todos si se usan herramientas como R y datos reales con muchos secretos por descubrir El lenguaje R es muy versátil y se puede usar en diferentes áreas del conocimientonombres2 = c('Juan', 'María', 'Pedro', 'Ana')
nombres2[1] "Juan" "María" "Pedro" "Ana" nombres3 = c("Juan", "María", "Pedro", 'Ana', 'Juan José')
nombres3[1] "Juan" "María" "Pedro" "Ana" "Juan José" [1] "Ana" "Ana" "Ana" "Beatriz" "Beatriz" "Beatriz" "Carmen" "Carmen" "Carmen" "Ana" "Ana"
[12] "Ana" "Beatriz" "Beatriz" "Beatriz" "Carmen" "Carmen" "Carmen" Para concatenar elementos de un vector de caracteres, se puede usar la función paste():
(pegado1 = paste("Nombre", 1:5))[1] "Nombre 1" "Nombre 2" "Nombre 3" "Nombre 4" "Nombre 5"(pegado2 = paste("Nombre", 1:5, sep = "_"))[1] "Nombre_1" "Nombre_2" "Nombre_3" "Nombre_4" "Nombre_5"(pegado3 = paste("Nombre", 1:5, collapse = ", "))[1] "Nombre 1, Nombre 2, Nombre 3, Nombre 4, Nombre 5"(pegado4 = paste("Nombre", 1:5, sep = "_", collapse = ", "))[1] "Nombre_1, Nombre_2, Nombre_3, Nombre_4, Nombre_5"También se puede utilizar la función paste0() para concatenar sin separador:
(pegado5 = paste0("Nombre", 1:5)) # equivale a: paste("Nombre", 1:5, sep = "")[1] "Nombre1" "Nombre2" "Nombre3" "Nombre4" "Nombre5"(pegado6 = paste0("Nombre", 1:5, collapse = ", "))[1] "Nombre1, Nombre2, Nombre3, Nombre4, Nombre5"Para crear un vector de longitud n con valores `, se puede usar la funcióncharacter()`:
vector_char = character(8)
vector_char[1] "" "" "" "" "" "" "" ""Se recomienda el uso de paquetes especializados en el tratamiento de vectores de tipo character, como stringr, stringi, glue.
5.3 Vectores de tipo factor
Los factores son variables categóricas en R que pueden ser ordinales (
ordered = TRUE) o nominales (ordered = FALSE).Los factores se pueden crear con la función
factor().Podemos imaginar que un factor es como un vector de enteros donde cada entero tiene una etiqueta.
[1] A B B A C B
Levels: A B C[1] A B B A C B
Levels: A < B < Cfactores[1] A B B A C B
Levels: A B C# Niveles del factor
(niveles = levels(factores))[1] "A" "B" "C"# Número de niveles del factor
(niveles = nlevels(factores))[1] 3# Número de elementos del factor
(niveles = length(factores))[1] 6# Es un factor?
(is.factor(factores))[1] TRUE# Es un factor ordenado?
(is.ordered(factores))[1] FALSEfactores4[1] Nivel 1 Nivel 2 Nivel 2 Nivel 1 Nivel 3 Nivel 2
Levels: Nivel 1 < Nivel 2 < Nivel 3(niveles4 = levels(factores4))[1] "Nivel 1" "Nivel 2" "Nivel 3"(is.ordered(factores4))[1] TRUESe pueden ver los valores enteros utilizados para asignar a las distintas categorías con unclass():
(factores5 = factor(c("A", "B", NULL, "A", "C", "B"),
levels = c("A", "B", "C"), ordered = TRUE,
labels = c("Nivel 1", "Nivel 2", "Nivel 3"),
exclude = NULL))[1] Nivel 1 Nivel 2 Nivel 1 Nivel 3 Nivel 2
Levels: Nivel 1 < Nivel 2 < Nivel 3(factores6 = factor(c("A", "B", "B", "A", "C", "B"),
levels = c("A", "B", "C"), ordered = TRUE,
exclude = c("B"),
labels = c("Nivel 1", "Nivel 3")
))[1] Nivel 1 <NA> <NA> Nivel 1 Nivel 3 <NA>
Levels: Nivel 1 < Nivel 3Nota: se recomienda ver el apartado de “Errores al convertir factor a numérico” para obtener más información sobre la conversión de factores a otros tipos de objetos.
5.4 Vectores lógicos
Los vectores lógicos se pueden crear con la función
c()o con operadores lógicos como==,!=,>,<,>=,<=,&,|,!.Los valores lógicos en R son
TRUEyFALSE, o también se pueden utilizar las abreviaturas:TyF, respectivamente.
(logicos = c(TRUE, FALSE, TRUE, TRUE, FALSE))[1] TRUE FALSE TRUE TRUE FALSE(logicos2 = c(1:5 > 3))[1] FALSE FALSE FALSE TRUE TRUE(logicos3 = c(1:5 == 3))[1] FALSE FALSE TRUE FALSE FALSE(logicos4 = c(1:5 != 3))[1] TRUE TRUE FALSE TRUE TRUE(logicos5 = c(1:5 >= 3))[1] FALSE FALSE TRUE TRUE TRUE(logicos6 = c(1:5 <= 3))[1] TRUE TRUE TRUE FALSE FALSE(logicos7 = c( (1:5 < 3) | (1:5 > 3) ))[1] TRUE TRUE FALSE TRUE TRUE(logicos8 = c( (1:5 < 3) & (1:5 > 3) ))[1] FALSE FALSE FALSE FALSE FALSE5.5 Vectores de fechas
Los vectores de fechas se pueden crear con la función
as.Date().Los formatos de fecha se pueden especificar con el argumento
format.El argumento
originse puede utilizar para especificar la fecha de origen.R considera siempre el formato
año-mes-día(ISO 8601) como el formato por defecto.
5.5.1 Uso: as.Date()
[1] "2021-01-01" "2021-01-02" "2021-01-03"str(fechas) Date[1:3], format: "2021-01-01" "2021-01-02" "2021-01-03"[1] "2021-01-01" "2021-02-01" "2021-03-01"[1] "2021-01-01" "2021-01-02" "2021-01-03"(fechas4 = as.Date(c("01-01-2021", "02-01-2021", "03-01-2021"),
format = "%d-%m-%Y",
origin = "1970-01-01"))[1] "2021-01-01" "2021-01-02" "2021-01-03"Se recomienda el uso de paquetes espcializados en el tratamiento de vectores de tipo fecha, como lubridate.
5.6 Información sobre vectores
- Para obtener información sobre un vector, se pueden usar funciones como
length(),class(),str(),summary(),table(), …
# Longitud del vector o número de elementos
length(proceso_A)[1] 65.7 Generación aleatoria de vectores
Las variables numéricas generadas aleatoriamente (num_var1, …) en el ejemplo introductorio se pueden crear con ayuda de funciones R como: sample(), rnorm(), runif(), rpois(), rexp(), rbinom(), …
Cuando se usan números aleatorios se recomienda fijar la semilla con set.seed() para poder reproducir los resultados.
set.seed(321)Para generar una muestra aleatoria de un vector, se puede usar la función sample():
(muestra0 = sample(1:10)) [1] 6 2 5 8 1 9 4 7 10 3(muestra0b = sample(10)) # equivale a sample(1:10) [1] 9 2 7 6 1 10 3 4 5 8(muestra = sample(1:10, 5))[1] 7 2 4 8 10(muestra2 = sample(1:10, 5, replace = TRUE))[1] 3 7 1 9 7 [1] 5 5 3 3 5 5 5 3 5 5(num_var3a <- sample(1:10, 10, replace = TRUE)) # Variable numérica entera [1] 4 1 7 3 3 4 2 6 3 9Para generar una muestra de una distribución normal, se puede usar la función rnorm():
(muestra_N = rnorm(5))[1] -1.53665329 0.07815779 0.25039581 0.24408720 0.79973823(muestra_N2 = rnorm(5, mean = 10, sd = 2))[1] 10.682819 10.517435 11.907757 12.272829 8.031424(num_var1a <- rnorm(10)) # Variable numérica normal [1] -0.9096546 -0.8890920 -0.2493402 0.3208509 -0.6653694 -1.0089165 0.3412016 0.3883978 1.7701642 0.2126621(num_var7a <- rnorm(10, mean = 0, sd = 10)) # Variable numérica con alta varianza [1] 14.6201732 0.5515576 12.4817840 -9.9804178 11.7091433 -24.9658225 -3.9314577 -1.6344373 7.0882276
[10] -11.6228043Para generar una muestra de una distribución uniforme, se puede usar la función runif():
(muestra_U = runif(5)) # valores entre 0 y 1[1] 0.1604628 0.2124876 0.3549263 0.5039408 0.4643445(muestra_U2 = runif(5, min = 10, max = 20)) # valores entre 10 y 20[1] 18.07924 16.44286 12.61307 16.89492 11.50505(num_var2a <- runif(nsim, min = 50, max = 100)) # Variable numérica uniforme [1] 71.50435 84.41629 86.12186 76.74178 96.00705 57.98855 85.73963 83.87464 76.47811 59.65561 60.83151 89.10906
[13] 82.76619 96.29860 77.39051 87.22977 62.80270 58.37344 95.38792 74.12483 55.64751 77.29796 51.70364 92.54096
[25] 61.65537 84.68197 73.56803 84.90016 73.37422 71.74467 53.49027 65.72362 70.69311 79.26368 88.41715 76.08448
[37] 54.49479 68.14155 61.12655 74.92482 99.44633 63.59462 86.81308 92.06125 87.87575 65.33611 75.35892 75.98626
[49] 61.39285 96.27045 54.81018 50.52183 58.95627 78.57928 93.57279 97.54909 89.66386 67.34334 56.00730 78.87341
[61] 73.23768 91.35798 91.93292 75.34809 87.22526 62.64531 70.77272 62.65265 68.29471 71.12346 52.94737 59.76778
[73] 84.91800 86.63021 79.92585 61.90592 83.22335 83.30048 96.93129 98.61857 81.60743 84.54094 69.53288 95.31510
[85] 78.30509 93.70527 57.51000 69.21227 69.47820 96.51903 91.61756 69.61340 60.54202 79.60581 61.92095 88.82752
[97] 57.53462 55.97985 86.12896 55.63331(num_var8a <- runif(10, min = -10, max = 10)) # Variable numérica con rango amplio [1] 6.427635 2.831651 1.870084 -1.751322 7.483651 -4.957212 1.812402 9.286923 -4.324252 -3.551845Para generar una muestra de una distribución de Poisson, se puede usar la función rpois():
(muestra_P = rpois(5, lambda = 3))[1] 3 2 6 2 5(num_var4a <- rpois(10, lambda = 3)) # Variable numérica de Poisson [1] 2 3 4 4 4 6 3 2 1 2Para generar una muestra de una distribución exponencial, se puede usar la función rexp():
(muestra_E = rexp(5, rate = 0.1))[1] 5.290092 10.305201 1.452451 3.117720 42.349405(num_var5a <- rexp(10, rate = 0.1)) # Variable numérica exponencial [1] 18.50301018 44.86541858 2.11917755 4.60555902 0.02192086 3.12258712 18.67214864 22.78281366 11.19506882
[10] 17.79928096Para generar una muestra de una distribución binomial, se puede usar la función rbinom():
(muestra_B = rbinom(5, size = 1, prob = 0.5))[1] 1 0 0 1 1(muestra_B2 = rbinom(5, size = 10, prob = 0.5))[1] 5 6 8 3 6(num_var6a <- rbinom(10, size = 1, prob = 0.5)) # Variable numérica binomial [1] 0 0 0 0 1 1 1 0 1 0 [1] "B" "B" "A" "C" "C" "C" "C" "C" "C" "C" [1] Categoría 1 Categoría 1 Categoría 2 Categoría 2 Categoría 1 Categoría 1 Categoría 1 Categoría 1 Categoría 2
[10] Categoría 1
Levels: Categoría 1 Categoría 2 [1] Grupo B Grupo A Grupo B Grupo B Grupo C Grupo C Grupo C Grupo C Grupo A Grupo B
Levels: Grupo A Grupo B Grupo C [1] Nivel 1 Nivel 2 Nivel 2 Nivel 2 Nivel 1 Nivel 1 Nivel 2 Nivel 1 Nivel 2 Nivel 2
Levels: Nivel 1 Nivel 2 [1] Tipo X Tipo Y Tipo Y Tipo Z Tipo Z Tipo Y Tipo Y Tipo Z Tipo Y Tipo Y
Levels: Tipo X Tipo Y Tipo ZSi cambiamos esa r por: d, p o q obtendríamos la función de densidad, la función de distribución o el cuantil (función inversa de la función de distribución) de las distintas distribuciones estadísticas. Por ejemplo para la distribución “Normal”: rnorm se tendrían: dnorm, pnorm, qnorm.
Ver más en: Sección 15.1
5.8 Ejercicios para practicar
- Crear un vector con los números del 1 al 10.
- Crear un vector con los números del 10 al 1.
6 Creación de matrices (matrix), data.frame y listas (list) en R
6.1 Creación de matrices (matrix) o arrays en R
6.1.1 Creación de matrices (matrix) en R
Las matrices en R se pueden crear con la función
matrix(). Son objetos de 2 dimensiones, donde todos sus datos son del mismo tipo: numéricos, o caracteres, o lógicos, …Para crear una matriz, se necesita un vector de datos (rellenará por columnas) y el número de filas y columnas.
# Crear una matriz con 3 filas y 4 columnas
(matriz1 = matrix(1:12, nrow = 3, ncol = 4)) [,1] [,2] [,3] [,4]
[1,] 1 4 7 10
[2,] 2 5 8 11
[3,] 3 6 9 12- Si se omite el número de filas o columnas, R intentará rellenar la matriz por columnas.
# Crear una matriz con 4 filas y 3 columnas
(matriz2 = matrix(1:12, nrow = 4)) [,1] [,2] [,3]
[1,] 1 5 9
[2,] 2 6 10
[3,] 3 7 11
[4,] 4 8 12- También se puede rellenar la matriz por filas con la opción
byrow = TRUE.
# Crear una matriz con 3 filas y 4 columnas
(matriz3 = matrix(1:12, nrow = 3, byrow = TRUE)) [,1] [,2] [,3] [,4]
[1,] 1 2 3 4
[2,] 5 6 7 8
[3,] 9 10 11 12m2 = matrix(1:3,nrow=3,ncol=2) # reciclado en R
m2 [,1] [,2]
[1,] 1 1
[2,] 2 2
[3,] 3 36.1.1.1 Información sobre matrices
6.1.2 Creación de arrays en R
Los arrays en R son objetos de más de 2 dimensiones (todos los datos tienen que ser del mismo tipo dentro de un array).
Para crear un array, se puede usar la función
array().
# Crear un array con 2 filas, 3 columnas, 2 matrices y 2 hipermatrices
(array2 = array(1:24, dim = c(2, 3, 2, 2))), , 1, 1
[,1] [,2] [,3]
[1,] 1 3 5
[2,] 2 4 6
, , 2, 1
[,1] [,2] [,3]
[1,] 7 9 11
[2,] 8 10 12
, , 1, 2
[,1] [,2] [,3]
[1,] 13 15 17
[2,] 14 16 18
, , 2, 2
[,1] [,2] [,3]
[1,] 19 21 23
[2,] 20 22 246.2 Creación de data.frames en R
Los data.frames en R son objetos de 2 dimensiones, donde cada columna puede ser de un tipo distinto.
Para crear un data.frame, se puede usar la función
data.frame().
# Crear un data.frame con 3 columnas con 3 vectores de longitud 3
(df1 = data.frame(
col1 = 1:4,
col2 = c("A", "B", "C","D"),
col3 = c(TRUE, FALSE, TRUE, TRUE)
)) col1 col2 col3
1 1 A TRUE
2 2 B FALSE
3 3 C TRUE
4 4 D TRUE- Se puede crear un data.frame a partir de una matriz. En este caso, todas las columnas del data.frame serán del mismo tipo, por la definición de un objeto tipo “matrix”.
(df2 = data.frame(
matrix(1:12, nrow = 3, ncol = 4)
)) X1 X2 X3 X4
1 1 4 7 10
2 2 5 8 11
3 3 6 9 12# Crear el data.frame
datos_a <- data.frame(respuesta, num_var1, num_var2, num_var3, num_var4, num_var5, num_var6,
num_var7, num_var8, factor_var1, factor_var2, factor_var3, factor_var4,
interaccion1, interaccion2)
dim(datos_a)[1] 100 15Si las columnas del data.frame son de distinto tipo, se puede convertir el data.frame en una matriz con la función as.matrix(), pero todas las columnas serán convertidas de forma automática para que todos los elementos de la matrix sean del mismo tipo (a caracteres, a numéricos, …).
# Crear una matriz a partir de un data.frame
(matriz1 = as.matrix(df1)) col1 col2 col3
[1,] "1" "A" "TRUE"
[2,] "2" "B" "FALSE"
[3,] "3" "C" "TRUE"
[4,] "4" "D" "TRUE" 6.3 Creación de listas en R
Las listas en R son objetos que pueden contener elementos de distinto tipo y distinta longitud. Se pueden incluir como elementos otros objetos R (vectores, matrices, data.frames, incluso otras listas, …).
Para crear una lista, se puede usar la función
list().
# Crear una lista con 3 elementos de distinto tipo
(lista1 = list(
num = 1:4,
char = c("A", "B", "C","D"),
log = c(TRUE, FALSE, TRUE, TRUE)
))$num
[1] 1 2 3 4
$char
[1] "A" "B" "C" "D"
$log
[1] TRUE FALSE TRUE TRUE- Se puede crear una lista a partir de un data.frame. En este caso, cada elemento de la lista será una columna del data.frame.
(lista2 = list(
data.frame(
matrix(1:12, nrow = 3, ncol = 4)
)
))[[1]]
X1 X2 X3 X4
1 1 4 7 10
2 2 5 8 11
3 3 6 9 12- Un data.frame es una lista especializada donde todos los elementos son vectores de la misma longitud, pero pueden ser vectores de distinto tipo.
7 Acceso a los elementos de un objeto R
-
Existen varios operadores que pueden usarse para extraer subconjuntos de objetos R:
[]siempre devuelve un objeto de la misma clase que el original; puede usarse para seleccionar más de un elemento.[[]]se usa para extraer elementos de una lista o de un data.frame; puede usarse para extraer un único elemento y la clase del objeto devuelto no necesariamente será una lista o data.frame.$se usa para extraer elementos de una lista o un data.frame por nombre; la semántica es similar a la de[[]].
7.1 Acceso a los elementos de un vector
(v1 = 1:10) [1] 1 2 3 4 5 6 7 8 9 10# Acceder al primer elemento
(v1[1])[1] 1# Acceder al último elemento
(v1[length(v1)])[1] 10# Acceder a los elementos 2, 4 y 6
(v1[c(2, 4, 6)])[1] 2 4 6# Acceder a los elementos 2 al 5
(v1[2:5])[1] 2 3 4 5# Acceder a los elementos 2 al 5 y 8
(v1[c(2:5, 8)])[1] 2 3 4 5 8# Acceder a todos los elementos menos el primero
(v1[-1])[1] 2 3 4 5 6 7 8 9 10# Acceder a todos los elementos menos las posiciones 2 y 4
(v1[-c(2, 4)])[1] 1 3 5 6 7 8 9 10(v2 = c("A" = 1, "B" = 2, "C" = 3, "D" = 4))A B C D
1 2 3 4 # Acceder al elemento con nombre "B"
(v2["B"])B
2 # Acceder a los elementos con nombre "A" y "C"
(v2[c("A", "C")])A C
1 3 # Acceder a los elementos con nombre "A" y "D" y "C"
(v2[c("A", "D", "C")])A D C
1 4 3 (v3 = 1:10) [1] 1 2 3 4 5 6 7 8 9 10# Acceder a los elementos mayores que 5
(v3[v3 > 5])[1] 6 7 8 9 10# Acceder a los elementos menores o iguales que 5
(v3[v3 <= 5])[1] 1 2 3 4 5# Acceder a los elementos iguales a 3 o 7
(v3[v3 == 3 | v3 == 7])[1] 3 7# Acceder a los elementos diferentes de 3 y 7
(v3[v3 != 3 & v3 != 7])[1] 1 2 4 5 6 8 9 10# Acceder a los elementos entre 3 y 7
(v3[v3 >= 3 & v3 <= 7])[1] 3 4 5 6 7# Acceder a los elementos pares
(v3[v3 %% 2 == 0])[1] 2 4 6 8 10# Acceder a los elementos impares
(v3[v3 %% 2 != 0])[1] 1 3 5 7 9(v4 = c(1, 2, NA, 4, 5))[1] 1 2 NA 4 5# Acceder a los elementos diferentes de NA
(v4[!is.na(v4)])[1] 1 2 4 5(v5 = c("a","b","c","d","d","a"))[1] "a" "b" "c" "d" "d" "a"(v5l = v5>"a")[1] FALSE TRUE TRUE TRUE TRUE FALSEv5[v5>"a"][1] "b" "c" "d" "d"7.2 Acceso a los elementos de una matriz
(matriz1 = matrix(1:12, nrow = 3, ncol = 4)) [,1] [,2] [,3] [,4]
[1,] 1 4 7 10
[2,] 2 5 8 11
[3,] 3 6 9 12- Para acceder a los elementos de una matriz, se puede usar la notación
matriz1[fila, columna].
# Acceder al elemento de la fila 2 y columna 3
(matriz1[2, 3])[1] 8- Para obtener los elementos de una fila o columna, se puede usar la notación
matriz1[fila, ]omatriz1[, columna].
# Acceder a la fila 2
(matriz1[2, ])[1] 2 5 8 11# Acceder a la columna 3
(matriz1[, 3])[1] 7 8 9- Se puede acceder a un subconjunto de filas o columnas con la notación
matriz1[fila1:fila2, columna1:columna2]o usando la funciónc():matriz1[fila1:fila2, c(columnai,columnaj)].
# Acceder a las filas 1 y 2 y columnas 4 y 2
(matriz1[1:2, c(4, 2)]) [,1] [,2]
[1,] 10 4
[2,] 11 5- Se puede usar el signo
-para excluir filas o columnas.
# Acceder a todas las filas menos la primera
(matriz1[-1, ]) [,1] [,2] [,3] [,4]
[1,] 2 5 8 11
[2,] 3 6 9 12# Acceder a todas las columnas menos las dos últimas
(matriz1[, -c(3, 4)]) [,1] [,2]
[1,] 1 4
[2,] 2 5
[3,] 3 6## Acceso a los elementos de un data.frame# Crear un data.frame con 3 filas y 4 columnas
(datos1 = data.frame(A = 1:3,
B = c("A", "B", "C"),
C = c(TRUE, FALSE, TRUE),
D = c(1.1, 2.2, 3.3))) A B C D
1 1 A TRUE 1.1
2 2 B FALSE 2.2
3 3 C TRUE 3.3# Acceder a la primera fila
(datos1[1, ]) A B C D
1 1 A TRUE 1.1# Acceder a la segunda columna
(datos1[, 2])[1] "A" "B" "C"# Acceder a la celda de la fila 2 y columna 3
(datos1[2, 3])[1] FALSE# Acceder a la columna "B"
(datos1[["B"]])[1] "A" "B" "C"# Acceder a la celda de la fila 2 y columna "C"
(datos1[2, "C"])[1] FALSE# Acceder a la celda de la fila 2 y columna "B"
(datos1[2, "B"])[1] "B"# Acceder a la columna "B"
(datos1$B)[1] "A" "B" "C"# Acceder a la celda de la fila 2 y columna "C"
(datos1$C[2])[1] FALSE# Acceder a la celda de las filas: 3 y 2 y columna "B"
(datos1$B[c(3,2)])[1] "C" "B"# Acceder a las filas con valores TRUE en la columna "C"
(datos1[datos1$C, ]) A B C D
1 1 A TRUE 1.1
3 3 C TRUE 3.3# Acceder a las filas con valores FALSE en la columna "C"
(datos1[!datos1$C, ]) A B C D
2 2 B FALSE 2.2 A B C D
1 1 A TRUE 1.1
3 3 C TRUE 3.3# Acceder a las filas con valores "B" en la columna "B" y "TRUE" en la columna "C"
(datos1[datos1$B == "B" & datos1$C, ])[1] A B C D
<0 rows> (or 0-length row.names)# Acceder a las filas con valores "B" en la columna "B" o "TRUE" en la columna "C"
(datos1[datos1$B == "B" | datos1$C, ]) A B C D
1 1 A TRUE 1.1
2 2 B FALSE 2.2
3 3 C TRUE 3.3# Acceder a las filas con valores "B" en la columna "B" y "FALSE" en la columna "C"
(datos1[datos1$B == "B" & !datos1$C, ]) A B C D
2 2 B FALSE 2.2 A B C D
1 1 A TRUE 1.1
3 3 C TRUE 3.3# Acceder a las filas con valores "B" en la columna "B" y "TRUE" en la columna "C"
(subset(datos1, B == "B" & C))[1] A B C D
<0 rows> (or 0-length row.names)# Acceder a las filas con valores "B" en la columna "B" o "TRUE" en la columna "C"
(subset(datos1, B == "B" | C)) A B C D
1 1 A TRUE 1.1
2 2 B FALSE 2.2
3 3 C TRUE 3.37.3 Acceso a los elementos de una lista
# Crear una lista con 3 elementos
(lista1 = list(num = 1:3,
char = c("A", "B", "C"),
log = c(TRUE, FALSE, TRUE)))$num
[1] 1 2 3
$char
[1] "A" "B" "C"
$log
[1] TRUE FALSE TRUE# Acceder al primer elemento
(lista1[[1]])[1] 1 2 3# Acceder al segundo elemento
(lista1[[2]])[1] "A" "B" "C"# Acceder al elemento con nombre "char"
(lista1[["char"]])[1] "A" "B" "C"# Acceder al elemento con nombre "log"
(lista1[["log"]])[1] TRUE FALSE TRUE# Acceder al elemento con nombre "num" pero solo a sus dos primeros elementos
(lista1[["num"]][1:2])[1] 1 2# Acceder al elemento con nombre "char"
(lista1$char)[1] "A" "B" "C"# Acceder al elemento con nombre "log"
(lista1$log)[1] TRUE FALSE TRUE# Acceder al elemento con nombre "num" pero solo a sus dos primeros elementos
(lista1$num[1:2])[1] 1 2# Extrae del primer elemento (un vector de integer), el tercer elemento
lista1[[c(1,3)]][1] 3# Extrae del segundo elemento (un vector de character), el segundo elemento
lista1[[c(2,2)]][1] "B"Equivalente a:
# Extrae del primer elemento, el tercer elemento
lista1[[1]][[3]][1] 3# Extrae del segundo elemento, el segundo elemento
lista1[[2]][[2]][1] "B"lista1[[2]][2][1] "B"Nota importante: la diferencia entre usar corchetes simples y corchetes dobles está en que
los corchetes dobles extraen el contenido de un único elemento de la lista (no tiene porque devolver un objeto de tipo lista),
mientras que los corchetes simples extraen una lista con uno o más elementos (siempre devuelve una lista).
# Acceder al primer elemento
(lista1[1])$num
[1] 1 2 3# Extraer el tercer y primer elemento
(subl01 = lista1[c(3,1)])$log
[1] TRUE FALSE TRUE
$num
[1] 1 2 3# Acceder a los elementos con valores TRUE en el tercer elemento
(lista1[[3]][lista1[[3]]])[1] TRUE TRUE# Acceder a los elementos con valores FALSE en el tercer elemento
(lista1[[3]][!lista1[[3]]])[1] FALSE# Acceder a los elementos con valores "A" o "C" en el segundo elemento
(lista1[[2]][lista1[[2]] %in% c("A", "C")])[1] "A" "C"# Acceder a los elementos con valores "B" en el segundo elemento y "TRUE" en el tercer elemento
(lista1[[2]][lista1[[2]] == "B"])[1] "B"# Acceder a los elementos con valores "B" en el segundo elemento o "TRUE" en el tercer elemento
(lista1[[2]][lista1[[2]] == "B" | lista1[[3]]])[1] "A" "B" "C"# Acceder a los elementos con valores "B" en el segundo elemento y "FALSE" en el tercer elemento
(lista1[[2]][lista1[[2]] == "B" & !lista1[[3]]])[1] "B"# Del segundo elemento, acceder a los elementos con valores "A" o "C"
# en el segundo elemento
(subset(lista1[[2]], lista1[[2]] %in% c("A", "C")))[1] "A" "C"# Del segundo elemento, acceder a los elementos con valores "B" en el segundo elemento
# y "TRUE" en el tercer elemento
(subset(lista1[[2]], lista1[[2]] == "B" & lista1[[3]]))character(0)# Acceder a los elementos con valores "B" en el segundo elemento o "TRUE" en el tercer elemento
(subset(lista1[[2]], lista1[[2]] == "B" | lista1[[3]]))[1] "A" "B" "C"8 Asignar valores a los elementos de un objeto R
8.1 Asignar valores a los elementos de un vector
(v1 = 1:10) [1] 1 2 3 4 5 6 7 8 9 10# Cambiar el primer elemento por 100
(v1[1] = 100)[1] 100v1 [1] 100 2 3 4 5 6 7 8 9 10# Cambiar los elementos 2, 4 y 6 por 200
(v1[c(2, 4, 6)] = 200)[1] 200v1 [1] 100 200 3 200 5 200 7 8 9 10# Cambiar los elementos 2 al 5 por 300
(v1[2:5] = 300)[1] 300v1 [1] 100 300 300 300 300 200 7 8 9 10# Cambiar los elementos 2 al 5 y 8 por 400
(v1[c(2:5, 8)] = 400)[1] 400v1 [1] 100 400 400 400 400 200 7 400 9 10(v2 = c("A" = 1, "B" = 2, "C" = 3, "D" = 4))A B C D
1 2 3 4 # Cambiar el elemento con nombre "B" por 200
(v2["B"] = 200)[1] 200v2 A B C D
1 200 3 4 # Cambiar los elementos con nombre "A" y "C" por 300
(v2[c("A", "C")] = 300)[1] 300v2 A B C D
300 200 300 4 (v3 = 1:10) [1] 1 2 3 4 5 6 7 8 9 10# Cambiar los elementos mayores que 5 por 500
(v3[v3 > 5] = 500)[1] 500v3 [1] 1 2 3 4 5 500 500 500 500 500# Cambiar los elementos menores o iguales que 5 por 600
(v3[v3 <= 5] = 600)[1] 600v3 [1] 600 600 600 600 600 500 500 500 500 500# Cambiar los elementos iguales a 3 o 7 por 700
(v3[v3 == 3 | v3 == 7] = 700)[1] 700v3 [1] 600 600 600 600 600 500 500 500 500 500# Cambiar los elementos diferentes de 3 y 7 por 800
(v3[v3 != 3 & v3 != 7] = 800)[1] 800v3 [1] 800 800 800 800 800 800 800 800 800 8008.2 Asignar valores a los elementos de una matriz
(matriz1 = matrix(1:12, nrow = 3, ncol = 4)) [,1] [,2] [,3] [,4]
[1,] 1 4 7 10
[2,] 2 5 8 11
[3,] 3 6 9 12- Para asignar valores a los elementos de una matriz, se puede usar la notación
matriz1[fila, columna].
# Cambiar el elemento de la fila 2 y columna 3 por 100
(matriz1[2, 3] = 100)[1] 100matriz1 [,1] [,2] [,3] [,4]
[1,] 1 4 7 10
[2,] 2 5 100 11
[3,] 3 6 9 12- Para asignar valores a una fila o columna, se puede usar la notación
matriz1[fila, ]omatriz1[, columna].
# Cambiar la fila 2 por 200
(matriz1[2, ] = 200)[1] 200matriz1 [,1] [,2] [,3] [,4]
[1,] 1 4 7 10
[2,] 200 200 200 200
[3,] 3 6 9 12# Cambiar la columna 3 por 300
(matriz1[, 3] = 300)[1] 300matriz1 [,1] [,2] [,3] [,4]
[1,] 1 4 300 10
[2,] 200 200 300 200
[3,] 3 6 300 12- Se puede asignar valores a un subconjunto de filas o columnas con la notación
matriz1[fila1:fila2, columna1:columna2]o usando la funciónc():matriz1[fila1:fila2, c(columnai,columnaj)].
# Cambiar las filas 1 y 2 y columnas 4 y 2 por 400
(matriz1[1:2, c(4, 2)] = 400)[1] 400matriz1 [,1] [,2] [,3] [,4]
[1,] 1 400 300 400
[2,] 200 400 300 400
[3,] 3 6 300 128.3 Asignar valores a los elementos de un data.frame
# Crear un data.frame con 3 filas y 4 columnas
(datos1 = data.frame(A = 1:3,
B = c("A", "B", "C"),
C = c(TRUE, FALSE, TRUE),
D = c(1.1, 2.2, 3.3))) A B C D
1 1 A TRUE 1.1
2 2 B FALSE 2.2
3 3 C TRUE 3.3# Cambiar el primer elemento de la columna "A" por 100
(datos1[1, "A"] = 100)[1] 100datos1 A B C D
1 100 A TRUE 1.1
2 2 B FALSE 2.2
3 3 C TRUE 3.3# Cambiar el segundo elemento de la columna "B" por "X"
(datos1[2, "B"] = "X")[1] "X"datos1 A B C D
1 100 A TRUE 1.1
2 2 X FALSE 2.2
3 3 C TRUE 3.3# Cambiar el tercer elemento de la columna "C" por FALSE
(datos1[3, "C"] = FALSE)[1] FALSEdatos1 A B C D
1 100 A TRUE 1.1
2 2 X FALSE 2.2
3 3 C FALSE 3.3# Cambiar el elemento de la fila 2 y columna "A" por 200
(datos1[2, "A"] = 200)[1] 200datos1 A B C D
1 100 A TRUE 1.1
2 200 X FALSE 2.2
3 3 C FALSE 3.3# Cambiar el elemento de la fila 3 y columna "B" por "Y"
(datos1[3, "B"] = "Y")[1] "Y"datos1 A B C D
1 100 A TRUE 1.1
2 200 X FALSE 2.2
3 3 Y FALSE 3.3# Cambiar el elemento de la fila 1 y columna "C" por TRUE
(datos1[1, "C"] = TRUE)[1] TRUEdatos1 A B C D
1 100 A TRUE 1.1
2 200 X FALSE 2.2
3 3 Y FALSE 3.3# Cambiar el elemento de la fila 2 y columna "A" por 300
(datos1$A[2] = 300)[1] 300datos1 A B C D
1 100 A TRUE 1.1
2 300 X FALSE 2.2
3 3 Y FALSE 3.3# Cambiar el elemento de la fila 3 y columna "B" por "Z"
(datos1$B[3] = "Z")[1] "Z"datos1 A B C D
1 100 A TRUE 1.1
2 300 X FALSE 2.2
3 3 Z FALSE 3.3# Cambiar el elemento de la fila 1 y columna "C" por FALSE
(datos1$C[1] = FALSE)[1] FALSEdatos1 A B C D
1 100 A FALSE 1.1
2 300 X FALSE 2.2
3 3 Z FALSE 3.3# Cambiar los elementos con valores TRUE en la columna "C" por FALSE
(datos1[datos1$C, "C"] = FALSE)[1] FALSEdatos1 A B C D
1 100 A FALSE 1.1
2 300 X FALSE 2.2
3 3 Z FALSE 3.3# Cambiar los elementos con valores FALSE en la columna "C" por TRUE
(datos1[!datos1$C, "C"] = TRUE)[1] TRUEdatos1 A B C D
1 100 A TRUE 1.1
2 300 X TRUE 2.2
3 3 Z TRUE 3.3# Cambiar los elementos con valores "A" o "C" en la columna "B" por "Z"
(datos1[datos1$B %in% c("A", "C"), "B"] = "Z")[1] "Z"datos1 A B C D
1 100 Z TRUE 1.1
2 300 X TRUE 2.2
3 3 Z TRUE 3.3# Cambiar los elementos con valores "B" en la columna "B" y "TRUE" en la columna "C" por "W"
(datos1[datos1$B == "B" & datos1$C, "B"] = "W")[1] "W"datos1 A B C D
1 100 Z TRUE 1.1
2 300 X TRUE 2.2
3 3 Z TRUE 3.3# Cambiar los elementos con valores "B" en la columna "B" o "TRUE" en la columna "C" por "V"
(datos1[datos1$B == "B" | datos1$C, "B"] = "V")[1] "V"datos1 A B C D
1 100 V TRUE 1.1
2 300 V TRUE 2.2
3 3 V TRUE 3.3- Si se asigna un vector de longitud mayor que el número de elementos a cambiar, R producirá un error (no reciclará los valores). Si se asigna un vector de longitud menor que el número de elementos a cambiar, R también producirá un error (no reciclará los valores).
# datos1[,2] = c("X", "Y", "Z", "W") # producirá error
# datos1[,2] = c("X", "Y") # producirá error
datos1[,2] = c("X", "Y", "Z")-
Excepción. Si se asigna un vector de longitud 1, R asignará el mismo valor a todos los elementos.
- PELIGRO: En un data.frame, si se asigna un valor escalar a una fila, se asignará a todas las celdas de la fila, cambiando el tipo de datos de cada columna si es necesario.
# Cambiar los elementos de la fila 2 por 300
str(datos1)'data.frame': 3 obs. of 4 variables:
$ A: num 100 300 3
$ B: chr "X" "Y" "Z"
$ C: logi TRUE TRUE TRUE
$ D: num 1.1 2.2 3.3(datos1[2, ] = 300)[1] 300datos1 A B C D
1 100 X 1 1.1
2 300 300 300 300.0
3 3 Z 1 3.3str(datos1)'data.frame': 3 obs. of 4 variables:
$ A: num 100 300 3
$ B: chr "X" "300" "Z"
$ C: num 1 300 1
$ D: num 1.1 300 3.38.4 Asignar valores a los elementos de una lista
Se puede asignar valores a los elementos de una lista por posición o por nombre, de la misma forma que se hace con los vectores.
# Crear una lista con 3 elementos
(lista1 = list(A = 1:3,
B = c("A", "B", "C"),
C = c(TRUE, FALSE, TRUE)))$A
[1] 1 2 3
$B
[1] "A" "B" "C"
$C
[1] TRUE FALSE TRUE# Cambiar el primer elemento de la lista por 100
(lista1[[1]] = 100)[1] 100lista1$A
[1] 100
$B
[1] "A" "B" "C"
$C
[1] TRUE FALSE TRUE# Cambiar el segundo elemento de la lista por "X"
(lista1[[2]] = "X")[1] "X"lista1$A
[1] 100
$B
[1] "X"
$C
[1] TRUE FALSE TRUE# Cambiar el tercer elemento de la lista por FALSE
(lista1[[3]] = FALSE)[1] FALSElista1$A
[1] 100
$B
[1] "X"
$C
[1] FALSE# Cambiar el elemento con nombre "A" por 200
(lista1[["A"]] = 200)[1] 200lista1$A
[1] 200
$B
[1] "X"
$C
[1] FALSE# Cambiar el elemento con nombre "B" por "Y"
(lista1[["B"]] = "Y")[1] "Y"lista1$A
[1] 200
$B
[1] "Y"
$C
[1] FALSE# Cambiar el elemento con nombre "C" por TRUE
(lista1[["C"]] = TRUE)[1] TRUElista1$A
[1] 200
$B
[1] "Y"
$C
[1] TRUE# Cambiar el elemento con nombre "A" por 300
(lista1$A = 300)[1] 300lista1$A
[1] 300
$B
[1] "Y"
$C
[1] TRUE# Cambiar el elemento con nombre "B" por "Z"
(lista1$B = "Z")[1] "Z"lista1$A
[1] 300
$B
[1] "Z"
$C
[1] TRUE# Cambiar el elemento con nombre "C" por FALSE
(lista1$C = FALSE)[1] FALSElista1$A
[1] 300
$B
[1] "Z"
$C
[1] FALSE# Cambiar los elementos con valores TRUE por FALSE
(lista1[[3]] = FALSE)[1] FALSElista1$A
[1] 300
$B
[1] "Z"
$C
[1] FALSE# Cambiar los elementos con valores FALSE por TRUE
(lista1[[3]] = TRUE)[1] TRUElista1$A
[1] 300
$B
[1] "Z"
$C
[1] TRUE# Cambiar los elementos con valores "A" o "C" por "Z"
(lista1[[2]][lista1[[2]] %in% c("A", "C")] = "Z")[1] "Z"lista1$A
[1] 300
$B
[1] "Z"
$C
[1] TRUE# Cambiar los elementos con valores "B" y "TRUE" por "W"
(lista1[[2]][lista1[[2]] == "B" & lista1[[3]]] = "W")[1] "W"lista1$A
[1] 300
$B
[1] "Z"
$C
[1] TRUE# Cambiar los elementos con valores "B" o "TRUE" por "V"
(lista1[[2]][lista1[[2]] == "B" | lista1[[3]]] = "V")[1] "V"lista1$A
[1] 300
$B
[1] "V"
$C
[1] TRUE9 Añadir y eliminar elementos de un objeto R
9.1 Añadir elementos a un objeto
# Crear un vector con 3 elementos
(vector1 = 1:3)[1] 1 2 3# Añadir un elemento al final del vector
(vector1 = c(vector1, 4))[1] 1 2 3 4# Añadir un elemento al principio del vector
(vector1 = c(0, vector1))[1] 0 1 2 3 4# Crear una lista con 3 elementos
(lista1 = list(A = 1:3,
B = c("A", "B", "C"),
C = c(TRUE, FALSE, TRUE)))$A
[1] 1 2 3
$B
[1] "A" "B" "C"
$C
[1] TRUE FALSE TRUE# Añadir un elemento al final de la lista
(lista1$D = c(10, 20, 30))[1] 10 20 30lista1$A
[1] 1 2 3
$B
[1] "A" "B" "C"
$C
[1] TRUE FALSE TRUE
$D
[1] 10 20 30# Crear un data.frame con 3 filas y 3 columnas
(datos1 = data.frame(A = 1:3,
B = c("A", "B", "C"),
C = c(TRUE, FALSE, TRUE))) A B C
1 1 A TRUE
2 2 B FALSE
3 3 C TRUE A B C
1 1 A TRUE
2 2 B FALSE
3 3 C TRUE
4 10 X FALSEdatos1 A B C
1 1 A TRUE
2 2 B FALSE
3 3 C TRUE
4 10 X FALSE# Añadir una columna al final del data.frame
(datos1$D = c(100, 200, 300, 400))[1] 100 200 300 400datos1 A B C D
1 1 A TRUE 100
2 2 B FALSE 200
3 3 C TRUE 300
4 10 X FALSE 400# Crear una matrix de 3x3
(matrix1 = matrix(1:9, nrow = 3)) [,1] [,2] [,3]
[1,] 1 4 7
[2,] 2 5 8
[3,] 3 6 9# Añadir una fila al final de la matrix
(matrix1 = rbind(matrix1, 10:12)) [,1] [,2] [,3]
[1,] 1 4 7
[2,] 2 5 8
[3,] 3 6 9
[4,] 10 11 12# Añadir una columna al final de la matrix
(matrix1 = cbind(matrix1, 13:15)) [,1] [,2] [,3] [,4]
[1,] 1 4 7 13
[2,] 2 5 8 14
[3,] 3 6 9 15
[4,] 10 11 12 13# Añadir una columna al principio de la matrix
(matrix1 = cbind(16:18, matrix1)) [,1] [,2] [,3] [,4] [,5]
[1,] 16 1 4 7 13
[2,] 17 2 5 8 14
[3,] 18 3 6 9 15
[4,] 16 10 11 12 13# Añadir una fila al principio de la matrix
(matrix1 = rbind(19:21, matrix1)) [,1] [,2] [,3] [,4] [,5]
[1,] 19 20 21 19 20
[2,] 16 1 4 7 13
[3,] 17 2 5 8 14
[4,] 18 3 6 9 15
[5,] 16 10 11 12 139.2 Eliminar elementos de un objeto
# Crear un vector con 5 elementos
(vector1 = 1:5)[1] 1 2 3 4 5# Eliminar el primer elemento del vector
(vector1 = vector1[-1])[1] 2 3 4 5# Eliminar el último elemento del vector
(vector1 = vector1[-length(vector1)])[1] 2 3 4# Crear una lista con 5 elementos
(lista1 = list(A = 1:4,
B = c("A", "B", "C", "D", "E"),
C = c(TRUE, FALSE)))$A
[1] 1 2 3 4
$B
[1] "A" "B" "C" "D" "E"
$C
[1] TRUE FALSE# Eliminar el primer elemento de la lista
(lista1 = lista1[-1])$B
[1] "A" "B" "C" "D" "E"
$C
[1] TRUE FALSE# Eliminar el último elemento de la lista
(lista1 = lista1[-length(lista1)])$B
[1] "A" "B" "C" "D" "E"Uso de NULL para eliminar elementos de una lista.
# Eliminar el elemento con nombre "B" de la lista
(lista1$B = NULL)NULLlista1named list()# Crear un data.frame con 5 filas y 3 columnas
(datos1 = data.frame(A = 1:5,
B = c("A", "B", "C", "D", "E"),
C = c(TRUE, FALSE, TRUE, FALSE, TRUE))) A B C
1 1 A TRUE
2 2 B FALSE
3 3 C TRUE
4 4 D FALSE
5 5 E TRUE# Eliminar la primera fila del data.frame
(datos1 = datos1[-1, ]) A B C
2 2 B FALSE
3 3 C TRUE
4 4 D FALSE
5 5 E TRUE# Eliminar la última fila del data.frame
(datos1 = datos1[-nrow(datos1), ]) A B C
2 2 B FALSE
3 3 C TRUE
4 4 D FALSE# Eliminar la primera y tercera fila del data.frame
(datos1 = datos1[-c(1, 3), ]) A B C
3 3 C TRUE(datos1 = data.frame(A = 1:5,
B = c("A", "B", "C", "D", "E"),
C = c(TRUE, FALSE, TRUE, FALSE, TRUE))) A B C
1 1 A TRUE
2 2 B FALSE
3 3 C TRUE
4 4 D FALSE
5 5 E TRUE# Eliminar la primera columna del data.frame
(datos1 = datos1[, -1]) B C
1 A TRUE
2 B FALSE
3 C TRUE
4 D FALSE
5 E TRUE# Eliminar la última columna del data.frame
(datos1 = datos1[, -ncol(datos1)])[1] "A" "B" "C" "D" "E"También se pueden eliminar más de una columna a la vez.
9.2.0.1 Eliminar elementos NA de un data.frame
# Crear un data.frame con 5 filas y 3 columnas
(datos1 = data.frame(A = c(1, 2, NA, 4, 5),
B = c("A", "B", NA, "D", "E"),
C = c(TRUE, FALSE, NA, NA, TRUE),
D = rnorm(5))) A B C D
1 1 A TRUE 0.07050839
2 2 B FALSE 0.12928774
3 NA <NA> NA 1.71506499
4 4 D NA 0.46091621
5 5 E TRUE -1.26506123Uso de la función complete.cases() para identificar las filas sin NA.
complete.cases(datos1)[1] TRUE TRUE FALSE FALSE TRUE# Eliminar las filas con algún NA
(datos2a = datos1[complete.cases(datos1), ]) A B C D
1 1 A TRUE 0.07050839
2 2 B FALSE 0.12928774
5 5 E TRUE -1.26506123# Eliminar las columnas con algún NA
(quecolumnas = c(any(is.na(datos1$A)),
any(is.na(datos1$B)),
any(is.na(datos1$C)),
any(is.na(datos1$D))))[1] TRUE TRUE TRUE FALSE(datos2b = datos1[, !quecolumnas])[1] 0.07050839 0.12928774 1.71506499 0.46091621 -1.26506123# Obtener los datos sin NA en la columna primera
(datos2c = datos1[!is.na(datos1$A), ]) A B C D
1 1 A TRUE 0.07050839
2 2 B FALSE 0.12928774
4 4 D NA 0.46091621
5 5 E TRUE -1.26506123La función na.omit() elimina las filas con algún NA.
(datos2d = na.omit(datos1)) A B C D
1 1 A TRUE 0.07050839
2 2 B FALSE 0.12928774
5 5 E TRUE -1.26506123Se haría de una forma similar a los data.frame.
# Crear una matrix de 5x3
(matrix1 = matrix(1:15, nrow = 5)) [,1] [,2] [,3]
[1,] 1 6 11
[2,] 2 7 12
[3,] 3 8 13
[4,] 4 9 14
[5,] 5 10 15# Eliminar la primera fila de la matrix
(matrix1 = matrix1[-1, ]) [,1] [,2] [,3]
[1,] 2 7 12
[2,] 3 8 13
[3,] 4 9 14
[4,] 5 10 15# Eliminar la última fila de la matrix
(matrix1 = matrix1[-nrow(matrix1), ]) [,1] [,2] [,3]
[1,] 2 7 12
[2,] 3 8 13
[3,] 4 9 14# Eliminar la primera columna de la matrix
(matrix1 = matrix1[, -1]) [,1] [,2]
[1,] 7 12
[2,] 8 13
[3,] 9 14# Eliminar la última columna de la matrix
(matrix1 = matrix1[, -ncol(matrix1)])[1] 7 8 910 Importar y exportar datos en un data.frame
10.1 Importar datos
Se supone que tenemos un fichero de texto rectangular datos.txt con el siguiente contenido:
A B C
1 A TRUE
2 B FALSE
3 C TRUE
4 D FALSELos ficheros de datos se encuentran en la subcarpeta datos del proyecto.
# Importar datos de un fichero de texto rectangular
(datos.txt = read.table("datos/datos.txt")) V1 V2 V3
1 A B C
2 1 A TRUE
3 2 B FALSE
4 3 C TRUE
5 4 D FALSE# Importar datos de un fichero CSV (separador por defecto ",")
(datos.csv = read.csv("datos/datos.csv")) A1 B1 C1
1 2.3 13.4 Juan
2 1.2 5.3 Pedro
3 3.4 7.2 Maria# Importar datos de un fichero CSV (separador ";")
(datos.csv2 = read.csv2("datos/datos2.csv")) notaEj01 notaEj02 Nombre
1 2.3 13.4 Juan
2 1.2 5.3 Pedro
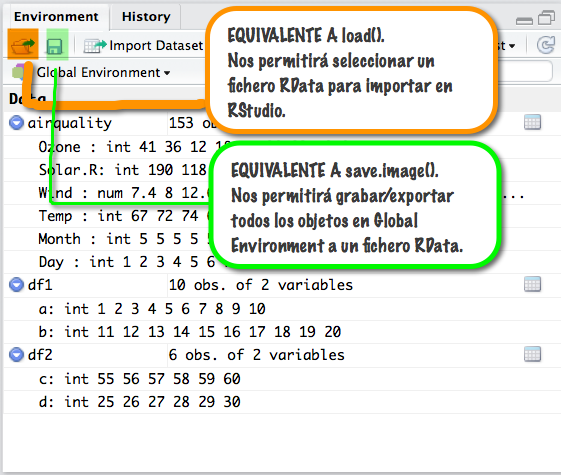
3 3.4 7.2 Maria# Importar datos de un fichero RData
load("datos/datos2expM.RData")# Importar datos de un fichero RData mostrando los objetos que contiene
load("datos/datos2expM.RData", verbose = TRUE)Loading objects:
datos.txt
datos.csv
datos.csv2# Instalar el paquete "readxl" si no está instalado
if (!requireNamespace("readxl", quietly = TRUE)) {
install.packages("readxl")
}# Importar datos de un fichero Excel con el paquete: "readxl"
(datos.xlsx = readxl::read_excel("datos/datos.xlsx",
sheet = 1, col_names = TRUE))# A tibble: 4 × 3
A B C
<chr> <chr> <chr>
1 1 A TRUE
2 2 B FALSE
3 3 C TRUE
4 4 D FALSE# Importar datos de un fichero Excel con el paquete: "rio"
if (!requireNamespace("rio", quietly = TRUE)) {
install.packages("rio")
}# Importar datos de un fichero Excel con el paquete: "rio"
(datos.xlsx2 = rio::import("datos/datos.xlsx",
sheet = 1, col_names = TRUE)) A B C
1 1 A TRUE
2 2 B FALSE
3 3 C TRUE
4 4 D FALSE Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
4 4.6 3.1 1.5 0.2 setosa
5 5.0 3.6 1.4 0.2 setosa
6 5.4 3.9 1.7 0.4 setosa# Importar el dataset "mtcars" del paquete "datasets"
datos.mtcars = datasets::mtcars
head(datos.mtcars) mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1attach(). Permite acceder a las variables de un data.frame sin tener que escribir el nombre del data.frame.detach(). Permite dejar de acceder a las variables de un data.frame.
# Usamos el data.frame: data.mtcars
attach(datos.mtcars)# Acceder a la variable "mpg" sin tener que escribir "datos.mtcars$mpg"
mpg [1] 21.0 21.0 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 17.8 16.4 17.3 15.2 10.4 10.4 14.7 32.4 30.4 33.9 21.5 15.5 15.2
[24] 13.3 19.2 27.3 26.0 30.4 15.8 19.7 15.0 21.4# Dejar de acceder a las variables de "datos.mtcars"
detach(datos.mtcars)10.2 Exportar datos
Se supone que tenemos un data.frame llamado datos.txt con el siguiente contenido, y que iremos guardarlo o exportarlo en distintos formatos de fichero en la subcarpeta datos del proyecto.
(datos.txt = data.frame(A = 1:4,
B = c("A", "B", "C", "D"),
C = c(TRUE, FALSE, TRUE, FALSE))) A B C
1 1 A TRUE
2 2 B FALSE
3 3 C TRUE
4 4 D FALSE# Exportar datos a un fichero de texto rectangular
write.table(datos.txt, "datos/datos2exp.txt", row.names = FALSE)# Exportar datos a un fichero CSV
write.csv(datos.csv, "datos/datos2exp.csv", row.names = FALSE)# Exportar datos a un fichero CSV con separador ";"
write.csv2(datos.csv2, "datos/datos2exp2.csv", row.names = FALSE)# Exportar un objeto a un fichero RData
save(datos.txt, file = "datos/datos2exp.RData")# Exportar varios objetos a un fichero RData
save(datos.txt, datos.csv, datos.csv2, file = "datos/datos2expM.RData")# Exportar todos los objetos a un fichero RData
save.image("datos/datos2expT.RData")# Exportar datos a un fichero Excel con el paquete: "rio"
rio::export(datos.xlsx, "datos/datos2exp.xlsx", col.names = TRUE)11 Operaciones y manipulación con objetos R
11.1 Operaciones con vectores
11.1.1 Operaciones elementos a elementos (o vectorizadas)
# Crear dos vectores
(v1 = 1:5)[1] 1 2 3 4 5(v2 = 6:10)[1] 6 7 8 9 10# Suma de dos vectores
(v1 + v2)[1] 7 9 11 13 15# Resta de dos vectores
(v3b = v1 - v2)[1] -5 -5 -5 -5 -5# Multiplicación de dos vectores
(v3c = v1 * v2)[1] 6 14 24 36 50# División de dos vectores
(v3d = v1 / v2)[1] 0.1666667 0.2857143 0.3750000 0.4444444 0.500000011.1.2 Operaciones con vectores y escalares
# Suma de un vector y un escalar
(v1 + 10)[1] 11 12 13 14 15# Resta de un vector y un escalar
(v1 - 10)[1] -9 -8 -7 -6 -5# Multiplicación de un vector y un escalar
(v4c = v1 * 10)[1] 10 20 30 40 50# División de un vector y un escalar
(v4d = v1 / 10)[1] 0.1 0.2 0.3 0.4 0.511.1.3 Operaciones con vectores lógicos
# Crear dos vectores lógicos
(v5 = c(TRUE, FALSE, TRUE, FALSE, TRUE))[1] TRUE FALSE TRUE FALSE TRUE(v6 = c(FALSE, TRUE, FALSE, TRUE, FALSE))[1] FALSE TRUE FALSE TRUE FALSE# Operador lógico "AND" de dos vectores
(v5 & v6)[1] FALSE FALSE FALSE FALSE FALSE# Operador lógico "OR" de dos vectores
(v7b = v5 | v6)[1] TRUE TRUE TRUE TRUE TRUE# Operador lógico "NOT" de un vector
(!v5)[1] FALSE TRUE FALSE TRUE FALSEx = 1:4; y = 6:9 # Atención al ";" para separar instrucciones
v8 = (y==8) | (x>=2)
v8[1] FALSE TRUE TRUE TRUE11.1.4 Otras operaciones con vectores
# Crear interacciones entre variables
interaccion1a <- num_var1 * num_var3
interaccion2a <- num_var2 * as.numeric(factor_var1)# Generar la variable de respuesta con una combinación lineal de las predictoras e interacciones
respuesta_a <- 5 + 1.5 * num_var1 + 2 * num_var2 + 0.5 * num_var3 +
0.3 * num_var4 + 0.2 * num_var5 +
3 * as.numeric(factor_var1) + 2 * as.numeric(factor_var2) +
interaccion1 + interaccion2 + rnorm(nsim)11.2 Operaciones con matrices y data.frame
11.2.1 Operaciones elementos a elementos
# Crear dos matrices
(matriz1 = matrix(1:9, nrow = 3)) [,1] [,2] [,3]
[1,] 1 4 7
[2,] 2 5 8
[3,] 3 6 9(matriz2 = matrix(10:18, nrow = 3)) [,1] [,2] [,3]
[1,] 10 13 16
[2,] 11 14 17
[3,] 12 15 18# Suma de dos matrices
(matriz1 + matriz2) [,1] [,2] [,3]
[1,] 11 17 23
[2,] 13 19 25
[3,] 15 21 27# Resta de dos matrices
(matriz1 - matriz2) [,1] [,2] [,3]
[1,] -9 -9 -9
[2,] -9 -9 -9
[3,] -9 -9 -9# Multiplicación de dos matrices componente a componente
(matriz1 * matriz2) [,1] [,2] [,3]
[1,] 10 52 112
[2,] 22 70 136
[3,] 36 90 162# División de dos matrices componente a componente
(matriz1 / matriz2) [,1] [,2] [,3]
[1,] 0.1000000 0.3076923 0.4375000
[2,] 0.1818182 0.3571429 0.4705882
[3,] 0.2500000 0.4000000 0.500000011.2.2 Operaciones con matrices y escalares
# Suma de una matriz y un escalar
(matriz1 + 10) [,1] [,2] [,3]
[1,] 11 14 17
[2,] 12 15 18
[3,] 13 16 19# Resta de una matriz y un escalar
(matriz1 - 10) [,1] [,2] [,3]
[1,] -9 -6 -3
[2,] -8 -5 -2
[3,] -7 -4 -1# Multiplicación de una matriz y un escalar
(matriz1 * 10) [,1] [,2] [,3]
[1,] 10 40 70
[2,] 20 50 80
[3,] 30 60 90# División de una matriz y un escalar
(matriz1 / 10) [,1] [,2] [,3]
[1,] 0.1 0.4 0.7
[2,] 0.2 0.5 0.8
[3,] 0.3 0.6 0.911.2.3 Otras formas
- Operaciones con matrices lógicas
# Crear dos matrices lógicas
(matriz3 = matrix(c(TRUE, FALSE, TRUE, FALSE, TRUE, FALSE, TRUE, FALSE, TRUE), nrow = 3)) [,1] [,2] [,3]
[1,] TRUE FALSE TRUE
[2,] FALSE TRUE FALSE
[3,] TRUE FALSE TRUE [,1] [,2] [,3]
[1,] FALSE TRUE FALSE
[2,] TRUE FALSE TRUE
[3,] FALSE TRUE FALSE# Operador lógico "AND" de dos matrices
(matriz3 & matriz4) [,1] [,2] [,3]
[1,] FALSE FALSE FALSE
[2,] FALSE FALSE FALSE
[3,] FALSE FALSE FALSE- Operaciones con matrices y vectores
# Crear un vector
(v7 = 1:3)[1] 1 2 3# Suma de una matriz y un vector
(matriz1 + v7) [,1] [,2] [,3]
[1,] 2 5 8
[2,] 4 7 10
[3,] 6 9 12# Resta de una matriz y un vector
(matriz1 - v7) [,1] [,2] [,3]
[1,] 0 3 6
[2,] 0 3 6
[3,] 0 3 6# Multiplicación de una matriz y un vector
(matriz1 * v7) [,1] [,2] [,3]
[1,] 1 4 7
[2,] 4 10 16
[3,] 9 18 27# División de una matriz y un vector
(matriz1 / v7) [,1] [,2] [,3]
[1,] 1 4.0 7
[2,] 1 2.5 4
[3,] 1 2.0 3Operaciones con 2 data.frames (igual que con matrices)
Operaciones con data.frames y vectores (igual que con matrices)
11.3 Funciones para la manipulación de datos
11.3.1 Funciones matemáticas
# Crear un vector
(v8 = c(1, 2, 3, 4, 5))[1] 1 2 3 4 5# Función "sqrt" para calcular la raíz cuadrada de un vector
(sqrt(v8))[1] 1.000000 1.414214 1.732051 2.000000 2.236068# Función "log" para calcular el logaritmo natural de un vector
(log(v8))[1] 0.0000000 0.6931472 1.0986123 1.3862944 1.6094379# Función "log10" para calcular el logaritmo en base 10 de un vector
(log10(v8))[1] 0.0000000 0.3010300 0.4771213 0.6020600 0.6989700# Función "exp" para calcular el exponencial de un vector
(exp(v8))[1] 2.718282 7.389056 20.085537 54.598150 148.413159# Función "abs" para calcular el valor absoluto de un vector
(abs(v8))[1] 1 2 3 4 5- Otras funciones matemáticas son:
sin(),cos(),tan(),asin(),acos(),atan(),sinh(),cosh(),tanh(),asinh(),acosh(),atanh().
# Uso de R como una calculadora
(1 + 2) * 3 / 4[1] 2.25[1] 4.107013- La función
pmax()devuelve el máximo de los elementos de dos o más vectores.
# Máximo de dos vectores
(pmax(v9, v10))[1] 5 4 3 4 5La función
pmin()devuelve el mínimo de los elementos de dos o más vectores.Existen otras funciones matemáticas que realizan cálculos directos, como:
choose()que calcula el número combinatorio de dos números. Por ejemplo, para calcular el número combinatorio de 5 elementos tomados de 2 en 2
choose(5, 2)[1] 10- La función
factorial()calcula el factorial de un número. Por ejemplo, para calcular el factorial de 5
factorial(5)[1] 120- La función
gamma()calcula la función gamma de un número. Por ejemplo, para calcular la función gamma de 5
gamma(5)[1] 24- La función
beta()calcula la función beta de dos números. Por ejemplo, para calcular la función beta de 5 y 2
beta(5, 2)[1] 0.03333333- Existen otras funciones de este tipo (no pondremos ejemplos):
lgamma(),lbeta(),digamma(),trigamma(),lchoose(). Se puede encontrar la ayuda de estas funciones en la documentación de R.
11.3.2 Funciones de redondeo y truncamiento
# Función "round" para redondear un vector a un número de dígitos decimales
(round(c(1.123, 2.234, 3.345, 4.456, 5.567), 2))[1] 1.12 2.23 3.35 4.46 5.57[1] 1 2 3 4 5[1] 2 3 4 5 611.3.3 Funciones sobre matrices
[,1] [,2] [,3]
[1,] 16 4 17
[2,] 2 51 8
[3,] 13 6 9# Determinante de una matriz
(det(matriz1))[1] -4147# Inversa de una matriz
(inv1 = solve(matriz1)) [,1] [,2] [,3]
[1,] -0.09910779 -0.01591512 0.20135037
[2,] -0.02073788 0.01856764 0.02266699
[3,] 0.15698095 0.01061008 -0.19483964# Producto de una matriz por su inversa: `%*%`
(matriz1 %*% inv1) [,1] [,2] [,3]
[1,] 1.000000e+00 0.000000e+00 0
[2,] 2.220446e-16 1.000000e+00 0
[3,] 0.000000e+00 -1.387779e-17 1 [,1]
[1,] 0.47311309
[2,] 0.08439836
[3,] -0.40631782# equivalente a
solve(matriz1, b)[1] 0.47311309 0.08439836 -0.40631782# Transpuesta de una matriz
(t(matriz1)) [,1] [,2] [,3]
[1,] 16 2 13
[2,] 4 51 6
[3,] 17 8 9# Diagonal de una matriz
(diag(matriz1))[1] 16 51 9# Autovectores y autovalores de una matriz
(eigen(matriz1))eigen() decomposition
$values
[1] 52.956273 26.049879 -3.006152
$vectors
[,1] [,2] [,3]
[1,] -0.1907292 -0.8109871 0.65389286
[2,] -0.9634870 0.2365820 0.08711335
[3,] -0.1879232 -0.5350971 -0.7515553211.3.4 Funciones estadísticas
# Función "sum" para calcular la suma de un vector
sum(v8)[1] 15# Función "prod" para calcular el producto de un vector
prod(v8)[1] 120# Función "cumsum" para calcular la suma acumulada de un vector
cumsum(v8)[1] 1 3 6 10 15# Función "mean" para calcular la media de un vector
mean(v8)[1] 3# Función "median" para calcular la mediana de un vector
median(v8)[1] 3# Función "var" para calcular la cuasivarianza de un vector
var(v8)[1] 2.5# Función "sd" para calcular la cuasidesviación típica de un vector
sd(v8)[1] 1.581139# Función "min" para calcular el mínimo de un vector
min(v8)[1] 1# Función "max" para calcular el máximo de un vector
max(v8)[1] 5# Función "range" para calcular el rango de un vector
range(v8)[1] 1 5# Función "quantile" para calcular los cuantiles de un vector
quantile(v8, probs = c(0.25, 0.5, 0.75))25% 50% 75%
2 3 4 # Función "IQR" para calcular el rango intercuartílico de un vector
IQR(v8)[1] 2En el paquete fBasics se encuentran las funciones skewness() y kurtosis() para calcular el sesgo y la curtosis de un vector.
# Función "skewness" para calcular el sesgo de un vector
fBasics::skewness(v8)[1] 0
attr(,"method")
[1] "moment"# Función "kurtosis" para calcular la curtosis de un vector
fBasics::kurtosis(v8)[1] -1.912
attr(,"method")
[1] "excess"# Función "summary" para obtener un resumen de un vector
summary(v8) Min. 1st Qu. Median Mean 3rd Qu. Max.
1 2 3 3 4 5 11.3.5 Funciones de manipulación de datos
# Crear un vector
(v9 = sample(10, 8, replace = TRUE))[1] 6 1 10 4 9 7 8 5# Función "sort" para ordenar un vector
sort(v9)[1] 1 4 5 6 7 8 9 10# Función "order" para obtener los índices o posiciones de un vector para ordenarlo
order(v9) [1] 2 4 8 1 6 7 5 3v9[order(v9)] # obtenemos el vector ordenado[1] 1 4 5 6 7 8 9 10# Función "rank" para obtener los rangos de cada elemento de un vector
rank(v9)[1] 4 1 8 2 7 5 6 3Nota: en caso de empate se pueden usar diferentes métodos para obtener los rangos asociados en ese caso, para ello se puede utiilzar el argumento ties.method de la función rank() con las siguientes posibilidades: ties.method = c("average", "first", "last", "random", "max", "min"). Por defecto, se utiliza ties.method = "average".
(v9b = c(1,4,7,9,4))[1] 1 4 7 9 4sort(v9b)[1] 1 4 4 7 9rank(v9b) # ties.method = "average"[1] 1.0 2.5 4.0 5.0 2.5rank(v9b, ties.method = "first")[1] 1 2 4 5 3rank(v9b, ties.method = "last")[1] 1 3 4 5 2# Función "rev" para invertir un vector
(rev(v9))[1] 5 8 7 9 4 10 1 6# Función "unique" para obtener los valores únicos de un vector
(unique(c(1, 2, 3, 1, 2, 3, 1, 2, 3)))[1] 1 2 3# Función "which" para obtener los índices de los valores que cumplen una condición
(which(v9 > 2))[1] 1 3 4 5 6 7 8# Función "which.min" para obtener el índice del valor mínimo de un vector
(which.min(v9))[1] 2# Función "which.max" para obtener el índice del valor máximo de un vector
(which.max(v9))[1] 3# Función "match" para obtener los índices de los valores de un vector que coinciden con otro vector
(match(c(1, 2, 3), v9))[1] 2 NA NA# Función "cut" para dividir un vector en intervalos
(cut(v9, breaks = 2))[1] (5.5,10] (0.991,5.5] (5.5,10] (0.991,5.5] (5.5,10] (5.5,10] (5.5,10] (0.991,5.5]
Levels: (0.991,5.5] (5.5,10]Ver más sobre cut() más adelante en Sección 14.1, apartado “Para variables cuantitativas (agrupadas)”.
11.4 Manipulación de datos con el sistema base de R
# Crear un data.frame
(datos1 = data.frame(A = c(1, 2, 1, 4, 2),
B = c("C", "B", "A", "D", "E"),
C = c(TRUE, FALSE, TRUE, FALSE, TRUE))) A B C
1 1 C TRUE
2 2 B FALSE
3 1 A TRUE
4 4 D FALSE
5 2 E TRUE# Ordenar un data.frame por una columna
datos1[order(datos1$A), ] A B C
1 1 C TRUE
3 1 A TRUE
2 2 B FALSE
5 2 E TRUE
4 4 D FALSE# Ordenar un data.frame por dos columnas
datos1[order(datos1$A, datos1$B), ] A B C
3 1 A TRUE
1 1 C TRUE
2 2 B FALSE
5 2 E TRUE
4 4 D FALSEEl filtrado de filas y columnas puede hacerse por 2 métodos diferentes usando las funciones subset() o which().
La función which(), devuelve un vector de índices de columnas o filas que verifican la condición.
A continuación, en el siguiente código, eliminamos la columna ‘Temp’ del data.frame ‘airquality’ y se devuelven solamente las observaciones con ‘Day=1’.
Método 1:
subset(airquality,Day == 1, select = - Temp) # selecciona Day=1 y excluye 'Temp' Ozone Solar.R Wind Month Day
1 41 190 7.4 5 1
32 NA 286 8.6 6 1
62 135 269 4.1 7 1
93 39 83 6.9 8 1
124 96 167 6.9 9 1Método 2:
Ozone Solar.R Wind Month Day
1 41 190 7.4 5 1
32 NA 286 8.6 6 1
62 135 269 4.1 7 1
93 39 83 6.9 8 1
124 96 167 6.9 9 1Hay que señalar que which() es una función independiente, por lo tanto, debe usarse el nombre completo del objeto, por ejemplo, which(Day==1) no funcionaría, ya que no hay variable llamada ‘Day’.
Analice los siguientes ejemplos:
Es una actividad muy habitual en análisis de datos muestrear o subdividir los datos en: conjuntos de entrenamiento (o training, datos con los que se construyen los modelos) y conjuntos test (datos conocidos en los que los modelos son probados).
Vemos a continuación cómo pueden crearse los conjuntos entrenamiento y test con 70:30 del data.frame ‘airquality’.
set.seed(100)
trainIndex <- sample(c(1:nrow(airquality)),
size=nrow(airquality)*0.7, replace=F)
# anterior, obtiene índices del conjunto de entrenamiento
dt.train = airquality[trainIndex, ] # data.frame de entrenamiento
dt.test = airquality[-trainIndex, ] # data.frame test
head(dt.train) Ozone Solar.R Wind Temp Month Day
102 NA 222 8.6 92 8 10
112 44 190 10.3 78 8 20
151 14 191 14.3 75 9 28
4 18 313 11.5 62 5 4
55 NA 250 6.3 76 6 24
70 97 272 5.7 92 7 9head(dt.test) Ozone Solar.R Wind Temp Month Day
1 41 190 7.4 67 5 1
6 28 NA 14.9 66 5 6
10 NA 194 8.6 69 5 10
11 7 NA 6.9 74 5 11
13 11 290 9.2 66 5 13
17 34 307 12.0 66 5 17Se ha creado una muestra aleatoria del 70% de los índices filas del data.frame ‘airquality’ al indicar: ’size=nrow(airquality)*0.7’.
Los data.frame pueden ser fusionados por una variable columna común. Si la columna ‘by’ tiene diferentes nombres, estas pueden especificarse por los argumentos: ‘by.x’ y ‘by.y’. El inner/outer join, left y right join de las consultas SQL pueden llevarse a cabo con los argumentos de merge: ‘all’, ‘all.x’, ‘all.y’.
La operación de fusión de dos data.frame tiene como resultado un nuevo data.frame que combina la información a partir de columnas enlace o clave en ambos data.frame. En R pueden realizarse con ayuda de la función R “merge()”.
Se usarán los siguientes data.frame para realizar diferentes operaciones de fusión de ejemplo con merge().
set.seed(100)
df1 = data.frame(
StudentId = c(1:10),
Subject = sample(c("Matematicas", "Ciencias", "Arte"), 10, replace=T))
df2 = data.frame(
StudentNum = c(2, 4, 6, 12),
Sport = sample(c("Futbol", "Tenis", "Ajedrez"), 4, replace=T))df1
df2 StudentId Subject
1 1 Ciencias
2 2 Arte
3 3 Ciencias
4 4 Arte
5 5 Matematicas
6 6 Ciencias
7 7 Ciencias
8 8 Arte
9 9 Ciencias
10 10 Ciencias StudentNum Sport
1 2 Ajedrez
2 4 Tenis
3 6 Tenis
4 12 AjedrezOperaciones de fusión:
merge(df1,df2,by.x="StudentId",by.y = "StudentNum") # inner join StudentId Subject Sport
1 2 Arte Ajedrez
2 4 Arte Tenis
3 6 Ciencias Tenismerge(df1,df2,by.x="StudentId",by.y = "StudentNum",all.x = T) # left join StudentId Subject Sport
1 1 Ciencias <NA>
2 2 Arte Ajedrez
3 3 Ciencias <NA>
4 4 Arte Tenis
5 5 Matematicas <NA>
6 6 Ciencias Tenis
7 7 Ciencias <NA>
8 8 Arte <NA>
9 9 Ciencias <NA>
10 10 Ciencias <NA>merge(df1,df2,by.x="StudentId",by.y = "StudentNum",all.y = T) # right join StudentId Subject Sport
1 2 Arte Ajedrez
2 4 Arte Tenis
3 6 Ciencias Tenis
4 12 <NA> Ajedrezmerge(df1,df2,by.x="StudentId",by.y = "StudentNum",all = T) # outer join StudentId Subject Sport
1 1 Ciencias <NA>
2 2 Arte Ajedrez
3 3 Ciencias <NA>
4 4 Arte Tenis
5 5 Matematicas <NA>
6 6 Ciencias Tenis
7 7 Ciencias <NA>
8 8 Arte <NA>
9 9 Ciencias <NA>
10 10 Ciencias <NA>
11 12 <NA> Ajedrez11.5 El uso del sistema tidyverse para manipulación de datos
Para saber más sobre el sistema tidyverse ver la siguiente url: https://www.tidyverse.org.
En el siguiente enlace puede practicar con el sistema tidyverse respondiendo a una serie de preguntas sobre un dataset de compras de artículos de un comercio.
11.5.1 El paquete “dplyr”
Se cargan los datos que se van a utilizar (un objeto de tipo data.frame o tibble).
'data.frame': 3000 obs. of 10 variables:
$ ano.inicio : num 2006 2004 2003 2003 2005 ...
$ edad : num 18 24 45 43 50 54 44 30 41 52 ...
$ estado.civil : chr "soltero" "soltero" "casado" "casado" ...
$ raza : chr "blanca" "blanca" "blanca" "asiatica" ...
$ nivel.educacion: chr "No tiene bachillerato" "Graduado Universitario" "Algun Curso Universidad" "Graduado Universitario" ...
$ tipo.trabajo : chr "Industrial" "Servicios" "Industrial" "Servicios" ...
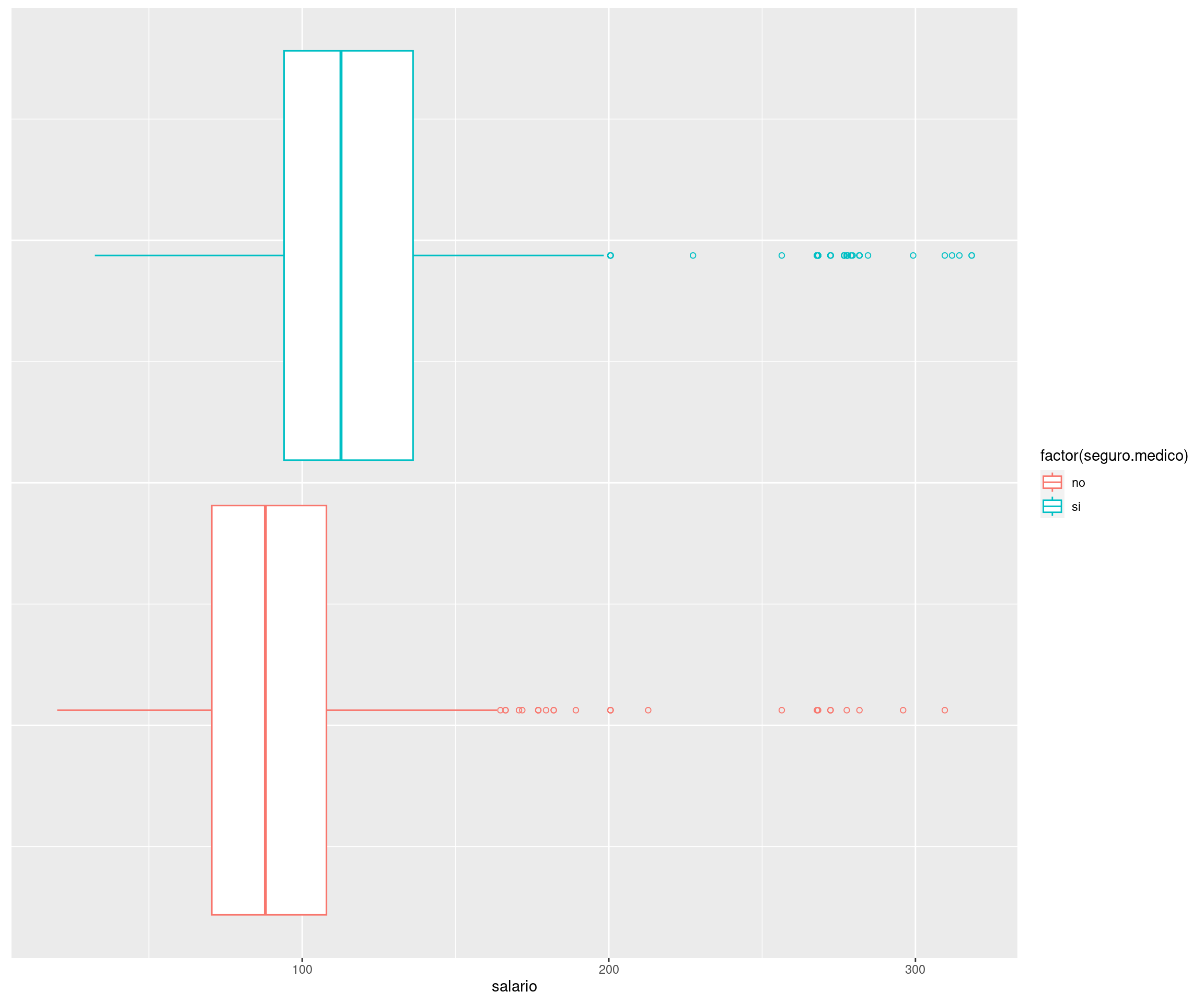
$ salud : chr "buena" "muy buena" "buena" "muy buena" ...
$ seguro.medico : chr "no" "no" "si" "si" ...
$ log.salario : num 4.32 4.26 4.88 5.04 4.32 ...
$ salario : num 75 70.5 131 154.7 75 ...# Uso de: filter(), select(), arrange() y slice()
datosF = datos.salarios |>
filter(ano.inicio==2006, # filtra filas
estado.civil=="casado" | estado.civil=="divorciado") |> # | representa "o"
select(raza,seguro.medico,salario) |> # selecciona cols
arrange(raza,desc(salario)) # ordena por cols
dim(datosF)[1] 296 3datosF |>
slice(1:2,12:14) # extrae filas concretas raza seguro.medico salario
1 asiatica si 148.4132
2 asiatica no 141.7752
3 blanca si 279.5018
4 blanca si 277.7995
5 blanca si 277.7995# Uso de: group_by(), rename(), mutate() (también: filter(), summarise())
datos.salarios %>%
filter(seguro.medico=='si' & estado.civil=='soltero') %>%
group_by(tipo.trabajo) %>%
summarise(
n = n(),
percent = n()/nrow(.)) %>%
rename(ni = n, fi = percent) %>%
mutate(pi = fi*100)# A tibble: 2 × 4
tipo.trabajo ni fi pi
<chr> <int> <dbl> <dbl>
1 Industrial 185 0.468 46.8
2 Servicios 210 0.532 53.2datos.salarios %>%
filter(seguro.medico=='si' & estado.civil=='soltero') %>%
group_by(tipo.trabajo) %>%
summarise(
MediaSalario = mean(salario),
MedianaSalario = median(salario),
MediaEdad = mean(edad),
MedianaEdad = median(edad)
)# A tibble: 2 × 5
tipo.trabajo MediaSalario MedianaSalario MediaEdad MedianaEdad
<chr> <dbl> <dbl> <dbl> <dbl>
1 Industrial 94.2 90.5 33.1 31
2 Servicios 112. 105. 36.0 33La función merge() del sistema base nos facilitó la fusión de dos data.frame. El sistema tidyverse también lo permite y además de una forma más eficiente.
Se usarán los mismos data.frame para realizar diferentes operaciones de fusión de ejemplo con el sistema tidyverse.
df1
df2 StudentId Subject
1 1 Ciencias
2 2 Arte
3 3 Ciencias
4 4 Arte
5 5 Matematicas
6 6 Ciencias
7 7 Ciencias
8 8 Arte
9 9 Ciencias
10 10 Ciencias StudentNum Sport
1 2 Ajedrez
2 4 Tenis
3 6 Tenis
4 12 AjedrezOperaciones de fusión:
df1 %>%
inner_join(df2, by = c("StudentId" = "StudentNum")) # inner join StudentId Subject Sport
1 2 Arte Ajedrez
2 4 Arte Tenis
3 6 Ciencias Tenisdf1 %>%
right_join(df2, by = c("StudentId" = "StudentNum")) # right join StudentId Subject Sport
1 2 Arte Ajedrez
2 4 Arte Tenis
3 6 Ciencias Tenis
4 12 <NA> AjedrezPara explicar la miniherramienta o función case_when(), se utilizan los siguientes datos que contienen personas que pertenecen o no a dos grupos: “Grupo1” y “Grupo2”.
df = data.frame(
Nombre = c("Juan","Ana","Marta"),
Grupo1 = c(F,T,T),
Grupo2 = c(F,F,T)
)
df Nombre Grupo1 Grupo2
1 Juan FALSE FALSE
2 Ana TRUE FALSE
3 Marta TRUE TRUESe utiliza la función case_when() para construir una nueva columna (mutate()) que asigne valores nuevos en función de los valores de las columnas: “Grupo1” y “Grupo2”. Como puede verse, aparecen una serie de expresiones lógicas a la izquierda del símbolo “~”, que si es cierta se asigna el valor que está a su derecha.
df <- df %>%
mutate(Grupo = case_when(
Grupo1 & Grupo2 ~ "A", # Ambos grupos: Grupo A
xor(Grupo1, Grupo2) ~ "B", # A un grupo solamente: Grupo B
!Grupo1 & !Grupo2 ~ "C", # Ningún grupo: Grupo C
TRUE ~ "D" # En otro caso: Grupo D (no habría otro caso)
))
df Nombre Grupo1 Grupo2 Grupo
1 Juan FALSE FALSE C
2 Ana TRUE FALSE B
3 Marta TRUE TRUE AMás adelante (ver Sección 14.3.1, en el apartado “Estadísticas agrupadas”) se muestra cómo se pueden realizar estas operaciones con el sistema base de R.
11.5.2 El paquete “tidyr”
Esta configuración de miniherramientas que usa el paquete dplyr invita a otros paquetes a extenderlo. Uno de tales paquetes es el paquete tidyr que forma parte del sistema “tidyverse”.
En general, el sistema tidyverse supone que cada fila es una observación, y cada columna es una variable. A esta disposición se la conoce como FORMATO LARGO.
En el siguiente ejemplo se presenta una situación diferente que aparece habitualmente. Hay una variable, lluvia o cantidad de precipitación, que se extiende sobre tres columnas (“lluvia_estacion01” a “lluvia_estacion03”). Esta disposición de los datos se conoce como FORMATO ANCHO.
set.seed(24)
dat = data.frame(temper = runif(3, 15, 25),
lluvia_estacion01 = runif(3, 1, 3),
lluvia_estacion02 = runif(3, 1, 3),
lluvia_estacion03 = runif(3, 1, 3))
dat temper lluvia_estacion01 lluvia_estacion02 lluvia_estacion03
1 17.92574 2.037794 1.559471 1.509450
2 17.24891 2.325239 2.527641 2.209778
3 22.04223 2.840888 2.603261 1.741470Como se ha comentado anteriormente, el sistema tidyverse espera que los datos se encuentren en “formato largo”. En algunas situaciones se necesita transformar los datos de “formato ancho” a “formato largo”. Es decir, en estos datos se necesita reunir todos los valores de precipitaciones en una única columna, y añadir una columna de identificación adicional que especifique la estación a la que pertenece.
La operación de combinación que convierte datos de formato ancho a formato largo puede realizarse usando la función pivot_longer() o también con gather().
pivot_longer(
data,
cols,
names_to = "name",
values_to = "value",
# más argumentos
...
)
#gather(data, key, value, ...)donde:
-
data, es el data.frame de entrada. -
names_to(key), el nombre de la columna con la identificación en el data.frame resultante. -
values_to(value), el nombre de la columna con los valores (precipitacion en nuestro ejemplo) en el data.frame resultante. -
cols(...), especificación de qué columnas deberían ser reunidas/combinadas. Se pueden usar nombres de columnas con un menos delante para excluir esas columnas de la combinación.
El siguiente código llama a pivot_longer() para transformar los datos del ejemplo anterior (aparece comentada el modo equivalente de hacerlo con la función: gather()).
library(tidyr)
dat_nuevos = dat %>%
pivot_longer(cols = -temper,
names_to = "id_estacion",
values_to = "precipitacion")
# dat_nuevos = gather(dat, key = id_estacion, value = precipitacion, -temper)
head(dat_nuevos)# A tibble: 6 × 3
temper id_estacion precipitacion
<dbl> <chr> <dbl>
1 17.9 lluvia_estacion01 2.04
2 17.9 lluvia_estacion02 1.56
3 17.9 lluvia_estacion03 1.51
4 17.2 lluvia_estacion01 2.33
5 17.2 lluvia_estacion02 2.53
6 17.2 lluvia_estacion03 2.21La operación contraria de extensión se realiza usando la función pivot_wider() o la función spread(), las cuales convierten de formato largo a formato ancho. En el siguiente ejemplo, se transforman a formato ancho los datos en formato largo creados en el apartado anterior: “dat_nuevos”.
pivot_wider(dat_nuevos,
names_from = "id_estacion",
values_from = "precipitacion")# A tibble: 3 × 4
temper lluvia_estacion01 lluvia_estacion02 lluvia_estacion03
<dbl> <dbl> <dbl> <dbl>
1 17.9 2.04 1.56 1.51
2 17.2 2.33 2.53 2.21
3 22.0 2.84 2.60 1.74#spread(dat_nuevos,key = id_estacion, value = precipitacion)La función separate() permite obtener nuevas columnas a partir de una columna de partida, al indicar una cadena de texto como separador. Por ejemplo, tenemos una columna fecha y queremos separarla en 3 columnas nuevas: día, mes y año.
Su complementario es unite(), que construye una nueva columna a partir de unir varias columnas con un separador que indiquemos.
Ejemplo. En la columna “Provincia” del conjunto de datos de población del censo de 2001 empleado anteriormente, aparece el código junto al nombre de la provincia separado por un guión.
#load("datosPobEspCenso2001.RData",verbose = TRUE)
set.seed(24)
datos2 = data.frame(
"Provincia" = c("01-Alava", "02-Albacete", "03-Alicante"),
lluvia_estacion01 = runif(3, 1, 3))
datos2 Provincia lluvia_estacion01
1 01-Alava 1.585148
2 02-Albacete 1.449782
3 03-Alicante 2.408446Para separarlo en dos columnas, se haría del siguiente modo:
datos_sep = datos2 %>%
separate(col = Provincia,into = c("Codigo","Provincia"),sep="-")
head(datos_sep) Codigo Provincia lluvia_estacion01
1 01 Alava 1.585148
2 02 Albacete 1.449782
3 03 Alicante 2.408446Por defecto, elimina la columna de partida, pero esto podría cambiarse (consultar la sintaxis de la función).
Ahora podría ordenarse por código o por el nombre de la provincia.
11.6 Uso de funciones de tipo bucle: apply, lapply, sapply
11.6.1 Función apply
La función apply() se utiliza para aplicar una función a los elementos de una matriz o array.
# Crear una matriz de 3x3
(matriz1 = matrix(1:9, nrow = 3)) [,1] [,2] [,3]
[1,] 1 4 7
[2,] 2 5 8
[3,] 3 6 9# Aplicar la función "mean" a las filas de la matriz
(apply(matriz1, 1, mean))[1] 4 5 6# Aplicar la función "mean" a las columnas de la matriz
(apply(matriz1, 2, mean))[1] 2 5 8
11.6.2 Función lapply
La función lapply() se utiliza para aplicar una función a los elementos de una lista.
# Crear una lista con dos vectores
(lista1 = list(1:3, 4:6))[[1]]
[1] 1 2 3
[[2]]
[1] 4 5 6# Aplicar la función "mean" a los elementos de la lista
(lapply(lista1, mean))[[1]]
[1] 2
[[2]]
[1] 5
11.6.3 Función sapply
La función sapply() es similar a lapply(), pero simplifica el resultado si es posible.
# Aplicar la función "mean" a los elementos de la lista
(sapply(lista1, mean))[1] 2 5# Aplicar la función "mean" a las filas de la matriz
(sapply(matriz1, mean))[1] 1 2 3 4 5 6 7 8 911.6.4 Otras funciones de tipo bucle
12 Construcción de funciones en R
12.1 Estructuras de control en R
- Las estructuras de control en R nos permiten controlar el flujo de ejecución del programa, dependiendo de las condiciones del tiempo de ejecución.
- Las estructuras más comunes son:
- if, else: comprueban una condición. switch.
- for: ejecuta un bucle un número fijo de veces.
- while: ejecuta un bucle mientras una condición sea verdadera.
- repeat: ejecuta un bucle infinito.
- break: finaliza la ejecución de un bucle.
- next: salta una iteración de un bucle.
- return: sale de una función.
- La mayoría de las estructuras de control no se usan en sesiones interactivas, sino al escribir funciones o expresiones grandes.
Operadores de comparación en R:
- igual: ==
- no igual: !=
- mayor/menor que: > <
- mayor/menor o igual que: >=, <=
Operadores lógicos en R:
- Y lógico: & (vectores) o && (escalares)
- O lógico: | (vectores) o || (escalares)
- NO lógico: !
if (<condicion>) {
# hacer algo
} else {
# hacer algo en otro caso
}
if (<condicion1>) {
# hacer algo
} else if (<condicion2>) {
# hacer algo diferente
} else {
# hacer algo diferente
}- Esto es una estructura if/else válida:
if (x>3) {
y = 10
} else {
y = 0
}- Esta también lo es:
y = if (x>3) {
10
} else {
0
}- La cláusula else no es necesaria:
if (<condicion1>) {
}
if (<condicion2>) {
}Nota: En la condición de las estructuras de control, en particular en las estructuras if, se pueden usar operadores lógicos y de comparación pero el resultado debe ser un escalar es decir un único valor TRUE o FALSE. Así que si se usa el “Y” o el “O” lógico, debe utilizarse && o || en lugar de & o |, ya que se producirían advertencias o errores.
Error in if ((c(3, 9) <= 2) & (c(9, 3) <= 2)) "Verdadero": the condition has length > 1Warning in (c(3, 9) <= 2) && (c(9, 3) <= 2): 'length(x) = 2 > 1' in coercion to 'logical(1)'Warning in (c(3, 9) <= 20) && (c(1, 3) <= 2): 'length(x) = 2 > 1' in coercion to 'logical(1)'Warning in (c(3, 9) <= 20) && (c(1, 3) <= 2): 'length(x) = 2 > 1' in coercion to 'logical(1)'[1] "Verdadero"Error in if ((c(3, 9) <= 20) & (c(1, 3) <= 2)) "Verdadero": the condition has length > 1Warning in (c(3, 9) <= 20) && (c(1, 3) <= 2): 'length(x) = 2 > 1' in coercion to 'logical(1)'
Warning in (c(3, 9) <= 20) && (c(1, 3) <= 2): 'length(x) = 2 > 1' in coercion to 'logical(1)'[1] TRUE[1] TRUE FALSEUso de las funciones: all() (si todos son verdaderos devuelve verdadero) y de any() (si alguno es verdadero devuelve verdadero) en R para evaluar expresiones lógicas vectoriales y que devuelvan un único valor lógico.
Uso de all():
Uso de any():
isTRUE()
La función isTRUE() se usa para verificar si un objeto es TRUE o no. Si el objeto es TRUE, devuelve TRUE, de lo contrario, devuelve FALSE.
La función ifelse() opera sobre vectores de longitud variable.
ifelse(test, valor_TRUE, valor_FALSE)Ejemplo:
x <- 1:10 # datos de ejemplo
ifelse(x<5 | x>8, x, 0) [1] 1 2 3 4 0 0 0 0 9 10- Para bucles se elige una variable iterador y asigna sus sucesivos valores de una secuencia o vector. Los bucles for son más usados para iterar sobre los elementos de un objeto (list, vector, etc)
for (i in 1:10) {
print(i)
}Este bucle selecciona la variable i y en cada iteración del bucle da los valores: 1, 2, 3, …, 10, y luego sale.
Estos tres bucles tienen el mismo comportamiento.
- Los bucles for pueden anidarse.
- Nota: ser cuidadoso con los bucles anidados, anidamientos de 2 o 3 niveles son más difíciles de leer/entender.
- Los bucles while comienzan probando una condición. Si es verdad (TRUE), entonces se ejecuta el cuerpo del bucle. Una vez que el cuerpo del bucle se ha ejecutado, la condición se prueba de nuevo, y así sucesivamente.
cuenta = 0
while (cuenta < 10) {
print(cuenta)
cuenta = cuenta + 1
}Bucles while pueden potencialmente resultar en bucles infinitos sino se escriben convenientemente. Deben usarse con cuidado.
Algunas veces podrá haber más de una condición que probar.
- Las condiciones son siempre evaluadas de izquierda a derecha.
- repeat inicia un bucle infinito; no se usa habitualmente en estadística pero tienen sus usos. El único camino de salir de un bucle repeat es llamando a break.
x <- 1
repeat {
print(x)
x = x+1
if (x == 6){
break
}
}x0 = 1
tol = 1e-8
repeat {
x1 = calculoEstimador()
if (abs(x1-x0)<tol) {
break
} else {
x0 = x1
}
} - El bucle anterior es un poco peligroso ya que no hay garantía que se detenga. Lo mejor es definir un límite fijo sobre el número de iteraciones (por ejemplo, usando for) y luego informar si la convergencia se alcanzó o no.
- next se usa para saltar una iteración de un bucle
for (i in 1:20) {
if (i==5) {
# Salta la iteración 5
next
}
print(i)
# hacer algo aquí
}- return indica que una función debe salir y devolver un valor dado.
12.2 Creación de funciones en R
- Las funciones se crean usando la directiva
function()y son almacenadas como objetos R exactamente igual que cualquier otro. En particular, son objetos R de la clase “function”.
f <- function(<argumentos>) {
# hacer algo interesante
}- Las funciones en R son “objetos de primera clase”, lo que significa que pueden considerarse como cualquier otro objeto R.
- Las funciones pueden ser pasadas como argumentos a otras funciones.
- Las funciones pueden ser anidadas, así que puede definirse una función dentro de otra función.
- El valor devuelto de una función es la última expresión en el cuerpo de la función que se evaluó.
- Los nombres de la función puede ser casi cualquier cosa. Sin embargo, debe evitarse el uso de nombres de funciones existentes.
- Reglas de alcance. Las variables creadas dentro de una función existen solamente en el tiempo de vida de la llamada a la función. Por lo que no son accesibles fuera de la función. Para forzar que variables en funciones sean vistas globalmente, puede usarse el operador de asignación global
<<-.
es.par <- function(un.numero){
resto <- un.numero %% 2
if (resto==0)
return(TRUE)
return(FALSE)
}
es.par(10)[1] TRUEes.par(9)[1] FALSEes.divisible.por <- function(numero.grande, numero.pequeno){
if (numero.grande %% numero.pequeno != 0)
return(FALSE)
return(TRUE)
}
es.divisible.por(10, 2)[1] TRUEes.divisible.por(10, 3)[1] FALSEes.divisible.por(9, 3)[1] TRUEes.par <- function(num){
es.divisible.por(num, 2)
}Más ejemplos de creación de funciones
myfct <- function(x1, x2=5) {
z1 <- x1/x1
z2 <- x2*x2
myvec <- c(z1, z2)
return(myvec)
}
myfct # imprime la definición de la funciónfunction(x1, x2=5) {
z1 <- x1/x1
z2 <- x2*x2
myvec <- c(z1, z2)
return(myvec)
}myfct(x1=2, x2=5) # aplica la función a los valores 2 y 5[1] 1 25myfct(2, 5) # los nombres de argumentos no serán necesarios, [1] 1 25 # pero el orden especificado es importante
myfct(x1=2) # igual que antes, pero el valor por defecto '5' se usa en este caso[1] 1 25- Los argumentos de las funciones R pueden encontrarse por posición o por nombre. Por ejemplo, las siguientes llamadas a la función
sdson todas equivalentes.
Aunque es legal, no se recomienda mezclar el orden de los argumentos mucho, ya que puede llevar a confusión.
Podemos mezclar búsqueda posicional con búsqueda por nombre. Cuando un argumento es encontrado por nombre, se “elige” de la lista de argumentos y los argumentos sin nombre que permanecen son buscados en el orden que son listados en la definición de la función.
args(lm)function (formula, data, subset, weights, na.action, method = "qr",
model = TRUE, x = FALSE, y = FALSE, qr = TRUE, singular.ok = TRUE,
contrasts = NULL, offset, ...)
NULL- Las siguientes dos llamadas son equivalentes.
La mayoría de las veces, los argumentos nombrados son útiles en la línea de comandos cuando tenemos una lista grande de argumentos y queremos usar los valores por defecto para cada cosa excepto para un argumento cercano al final de la lista.
Argumentos nombrados también ayudan a recordar el nombre del argumento y no su posición en la lista de argumentos (por ejemplo, la función
plot()es un buen ejemplo de eso).Definir una función
f = function(a, b=1, c=2, d=NULL) {
}Además para no especificar un valor por defecto, podemos también definir un valor de argumento igual a NULL.
- Los argumentos para las funciones son evaluados de forma perezosa, ya que se evalúan solamente cuando se necesita.
f = function(a, b) {
a^2
}
f(2)Esta función realmente nunca usa el argumento b, al llamar
f(2)no producirá ningún error ya que el 2 encuentra el argumento a por posición.Otro ejemplo
- Observa que “45” se imprime primero antes de que se produzca el lanzamiento del error. Esto es porque “b” no tiene que ser evaluado hasta después de “print(a)”. Una vez que la función intenta evaluar “print(b)” lanza el error.
- El argumento “…” indica un número variable de argumentos que son pasados realmente a otras funciones.
- “…” se usa habitualmente cuando extendemos otra función y no queremos copiar la lista de argumentos completa de la función original.
miplot = function(x, y, tipo=T, ...) {
plot(x,y,type=tipo,...)
}- Las funciones genéricas usan “…” para pasar argumentos extras a los métodos.
meanfunction (x, ...)
UseMethod("mean")
<bytecode: 0x55e1fea48320>
<environment: namespace:base>- El argumento “…” es también necesario cuando el número de argumentos pasado a la función no se puede conocer por adelantado.
- Un problema con “…” es que cualquier argumento que aparezca después de “…” sobre la lista de argumentos debe tener el nombre exacto y no parcialmente.
-
return: el flujo de evaluación de una función puede terminarse en cualquier parte con la funciónreturn(). Generalmente se usa con evaluaciones de condicionales. -
stop(): para detener la acción de una función y mostrar un mensaje de error, puede usarse la funciónstop. -
warning(): imprime un mensaje de aviso en situaciones inesperadas sin abortar el flujo de evaluación de la función.
12.3 Mejorando las funciones
Con la función
tryCatch()se consigue evitar que cuando se produzcan errores no se detenga el programa, en tal caso el programa lo captura y efectuará las operaciones que se le indiquen en tal situación.Cuando se producen warnings o avisos no se detiene el programa pero se emiten mensajes, lo que con esta función se podrían eliminar o personalizar.
Veamos un ejemplo básico de uso al crear una función que se encargará de importar un fichero excel.
importa_excel = function(ficheroexcel, hoja) {
resultado = tryCatch({
dframe <- readxl::read_excel(ficheroexcel, sheet = hoja)
cat("Ha ido todo bien\n")
return(dframe)
}, warning = function(w) {
cat(paste("Se ha producido un warning al intentar importar: ", ficheroexcel,"\n",w))
dframe = NULL
return(dframe)
}, error = function(e) {
cat(paste("Se ha producido un error al intentar importar: ", ficheroexcel,"\n",e))
dframe = NULL
return(dframe)
}, finally = {
cat("Ha finalizado\n")
}
)
return(resultado)
}
df1 = importa_excel("mtcars2no.xlsx",1)
# Se ha producido un error al intentar importar: mtcars2no.xlsx
# Ha ido todo bien
df2 = importa_excel("mtcars2.xlsx",1)
# Ha ido todo bienHay varias utilidades en R para hacer depuración (debugging) de código: debug(funcionR) (undebug(), debugonce()) y la más utilizada browser() (detiene la ejecución en los puntos de ruptura en el código donde se ha escrito).
En las siguientes capturas se muestra como RStudio facilita el uso de la depuración de código al encontrarse la función “browser()” (o punto de ruptura) en el cuerpo de una función incluida en un fichero de código R: “ejbrowser.R”.
En la consola de RStudio se han habilitado una barra de herramientas para la depuración de código con cinco iconos:
- “Next” (F10). Ejecuta la siguiente línea de código.
- “Step into current function” (May+F4). Entra en el interior de la función en la línea de código actual.
- “Execute the remainder of the current function or loop” (May+F7). Ejecuta el resto de la función actual o bucle.
- “Continue” (May+F5). Continúa la ejecución hasta el próximo punto de ruptura o “browser()” que se encuentre.
- “Stop” (May+F8). Sale del modo “debuging”.
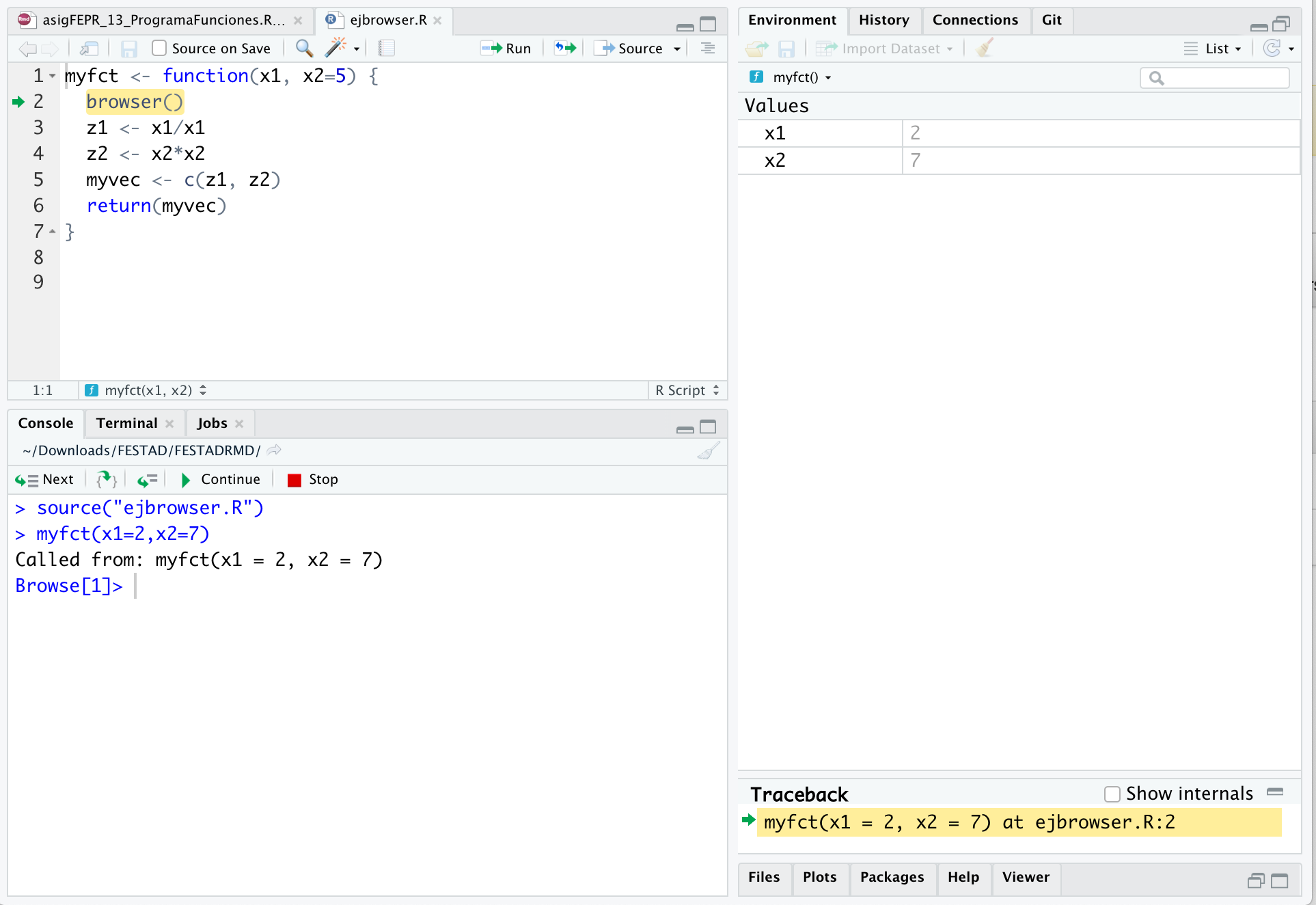
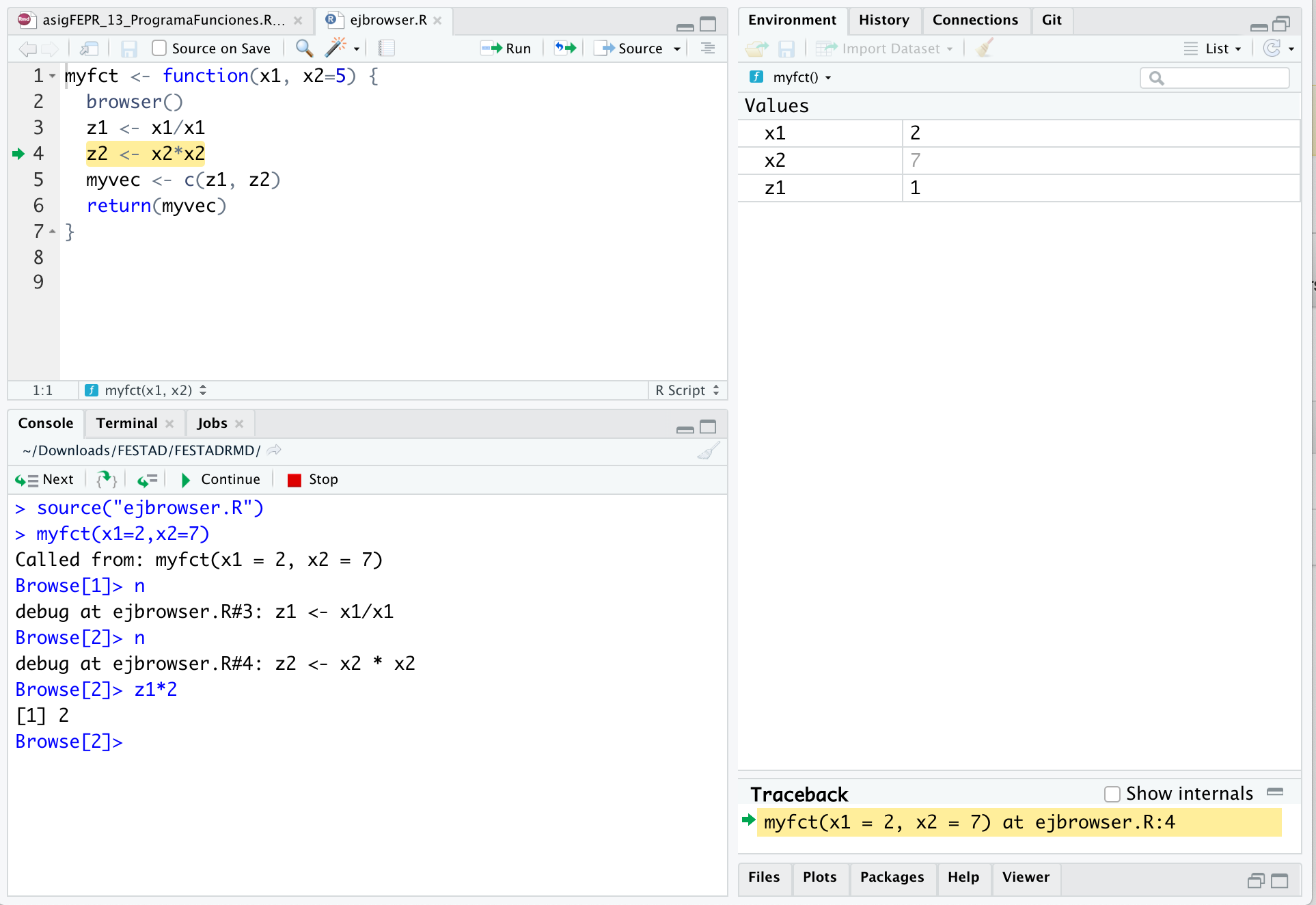
12.4 Ejemplos de funciones en R
12.4.1 Función para extraer los extremos de los intervalos obtenidos con cut
Extremos_IntervalosAgrup = function(num_var1, breaks_ = 5, dig.lab_ = 3) {
AgrupaenIntervalos = cut(num_var1, breaks = breaks_, dig.lab = dig.lab_)
ExtremosIntervalos = levels(AgrupaenIntervalos)
ExtremosIntervalos = gsub("\\(|\\]", "", ExtremosIntervalos)
ExtremosIntervalos = gsub(",", " - ", ExtremosIntervalos)
s1 = unlist(strsplit(ExtremosIntervalos, " - ", fixed = TRUE))
ExtremosIntervalos = unique(as.numeric(s1))
ExtremosIntervalos
}
(ExtIntervalos = Extremos_IntervalosAgrup(num_var1, breaks_ = 5))[1] -2.310 -1.410 -0.511 0.389 1.290 2.190[1] "(-2.31,-1.41]" "(-1.41,-0.511]" "(-0.511,0.389]" "(0.389,1.29]" "(1.29,2.19]" 12.4.2 Función para calcular el contraste sobre la varianza de una variable numérica
var_test_1var <- function(x, var0, alpha = 0.05) {
# Cálculos básicos
n <- length(x)
var_muestra <- var(x)
estadistico <- (n-1) * var_muestra / var0
df <- n-1
# P-valor bilateral
p_valor <- 2 * min(
pchisq(estadistico, df = df),
1 - pchisq(estadistico, df = df)
)
# Intervalos de confianza
chi_lower <- qchisq(alpha/2, df = df)
chi_upper <- qchisq(1-alpha/2, df = df)
ic_lower <- (n-1) * var_muestra / chi_upper
ic_upper <- (n-1) * var_muestra / chi_lower
# Resultados
resultados <- list(
estadistico = estadistico,
p_valor = p_valor,
varianza_muestra = var_muestra,
varianza_hipotesis = var0,
ic_lower = ic_lower,
ic_upper = ic_upper,
decision = ifelse(p_valor < alpha,
"Rechazar H0",
"No rechazar H0")
)
return(resultados)
}
var_test_1var(x = rnorm(12,sd = 4), var0 = 2, alpha = 0.05)$estadistico
[1] 83.74678
$p_valor
[1] 5.540013e-13
$varianza_muestra
[1] 15.22669
$varianza_hipotesis
[1] 2
$ic_lower
[1] 7.641113
$ic_upper
[1] 43.89534
$decision
[1] "Rechazar H0"12.4.3 Función para calcular el contraste la diferencia de proporciones de Bernouilli dependientes (test de McNemar)
test_mcnemar <- function(antes, despues, alpha = 0.05) {
# Crear tabla de contingencia
tabla <- table(antes, despues)
# Extraer valores
n12 <- tabla[1,2] # Cambios de 0 a 1
n21 <- tabla[2,1] # Cambios de 1 a 0
# Calcular estadístico
estadistico <- ((abs(n12 - n21) - 1)^2) / (n12 + n21)
# Calcular p-valor
p_valor <- pchisq(estadistico, df = 1, lower.tail = FALSE)
# Calcular proporción de cambios
n_total <- sum(tabla)
prop_antes <- sum(tabla[2,]) / n_total
prop_despues <- sum(tabla[,2]) / n_total
# Intervalo de confianza para la diferencia
diff_prop <- prop_despues - prop_antes
se_diff <- sqrt((n12 + n21)/(n_total^2))
z <- qnorm(1 - alpha/2)
ic_lower <- diff_prop - z * se_diff
ic_upper <- diff_prop + z * se_diff
return(list(
tabla = tabla,
estadistico = estadistico,
p_valor = p_valor,
prop_antes = prop_antes,
prop_despues = prop_despues,
diferencia = diff_prop,
ic_lower = ic_lower,
ic_upper = ic_upper,
decision = ifelse(p_valor < alpha, "Rechazar H0", "No rechazar H0")
))
}
# Ejemplo con datos pareados
antes <- c(1,1,0,1,0,1,1,0,0,1) # 1: éxito, 0: fracaso
despues <- c(1,1,1,1,0,0,1,1,1,1)
# Crear tabla de contingencia
tabla <- table(antes, despues)
# McNemar con la función definida en el paquete R: "stats"
(resultado <- mcnemar.test(tabla))
McNemar's Chi-squared test with continuity correction
data: tabla
McNemar's chi-squared = 0.25, df = 1, p-value = 0.6171# McNemar con la función creada
(resultado2 <- test_mcnemar(antes, despues))$tabla
despues
antes 0 1
0 1 3
1 1 5
$estadistico
[1] 0.25
$p_valor
[1] 0.6170751
$prop_antes
[1] 0.6
$prop_despues
[1] 0.8
$diferencia
[1] 0.2
$ic_lower
[1] -0.1919928
$ic_upper
[1] 0.5919928
$decision
[1] "No rechazar H0"13 Otras cuestiones de interés
13.1 Cómo dar nombre a las variables u objetos en R
Se pueden usar caracteres alfanuméricos, puntos y guiones bajos (distinguiendo entre mayúsculas y minúsculas), pero no se pueden empezar con un número ni contener espacios. Además, no se pueden usar palabras reservadas de R como nombres de variables, ni empezar con un punto seguido de un número.
proceso_Aproceso_A.1Proceso_A.1.proceso_B
1proceso_Aproceso Aproceso-A.1proceso_A
13.2 Valores especiales en R: NA, NULL, NaN, Inf y -Inf
En R, los valores faltantes se representan con
NA(Not Available).Si se intenta realizar una operación aritmética con un
NA, el resultado seráNA.Para comprobar si un valor es
NA, se puede usar la funciónis.na().
En R, el valor
NULLse usa para representar la ausencia de un objeto.Si se intenta realizar una operación aritmética con un valor
NULL, se producirá un error.Para comprobar si un valor es
NULL, se puede usar la funciónis.null().
# Crear un vector con un valor NULL
(v1 = c(1, 2, NULL, 4, 5))[1] 1 2 4 5# Comprobar si un valor es NULL
is.null(v1)[1] FALSE(v2 = is.null(v1))[1] FALSE- Si se asigna un valor
NULLa un objeto, se eliminará el objeto.
# Crear un vector con un valor NULL
v1 = c(1, 2, 3, 4, 5)
v1[1] 1 2 3 4 5# Asignar un valor NULL a un objeto
v1 = NULL
v1NULLEn R, los valores infinitos positivos y negativos se representan con
Infy-Inf, respectivamente.Si se intenta realizar una operación aritmética con un valor infinito, el resultado será
Info-Inf(no se producirá un error).
# Crear un vector con un valor infinito
(v1 = c(3/0, Inf, -10/0, -Inf, 72, 0.23))[1] Inf Inf -Inf -Inf 72.00 0.23- Para comprobar si un valor es infinito, se puede usar la función
is.infinite().
# Crear un vector con un valor infinito
(v1 = c(1, 2, Inf, 4, 5))[1] 1 2 Inf 4 5# Comprobar si un valor es Infinito
is.infinite(v1)[1] FALSE FALSE TRUE FALSE FALSE(v2 = is.infinite(v1))[1] FALSE FALSE TRUE FALSE FALSE13.3 Conocer de qué tipo es un objeto en R
- Para saber de qué tipo es un objeto en R, se puede usar la función
class().
- Para saber el tipo de datos de un objeto en R, se puede usar la función
typeof().
- Para obtener una descripción estructurada de un objeto en R, se puede usar la función
str().
- Para comprobar si un objeto es de un tipo concreto, se pueden usar las funciones
is.numeric(),is.integer(),is.character(),is.logical(),is.factor().
(v1 = 1:5)[1] 1 2 3 4 5is.numeric(v1)[1] TRUEis.integer(v1)[1] TRUEis.character(v1)[1] FALSEis.logical(v1)[1] FALSEis.factor(v1)[1] FALSE[1] TRUE13.4 Convertir vectores de unos tipos a otros
Para convertir un vector de un tipo a otro, se puede usar la función
as.numeric(),as.integer(),as.character(),as.logical(),as.factor(), …Si se intenta convertir un vector de caracteres a numérico y hay algún valor que no se puede convertir, se obtendrá un
NA.
# Convertir un vector numérico a un vector de caracteres
(v1 = 1:5)[1] 1 2 3 4 5(v2 = as.character(v1))[1] "1" "2" "3" "4" "5"# Convertir un vector de caracteres a un vector numérico
(v3 = c("1", "2", "3", "4", "hola"))[1] "1" "2" "3" "4" "hola"(v4 = as.numeric(v3)) # el último valor no se puede convertir coerción a NA[1] 1 2 3 4 NA# Convertir un vector de caracteres a un vector lógico
(v5 = c("TRUE", "FALSE", "T", "F", "3.32", "S"))[1] "TRUE" "FALSE" "T" "F" "3.32" "S" (v6 = as.logical(v5))[1] TRUE FALSE TRUE FALSE NA NA# Convertir un vector numérico a un vector lógico
(v7 = c(1, 0, 1, 0, 1, 23, -1, -7, 2.1, NA, Inf)) [1] 1.0 0.0 1.0 0.0 1.0 23.0 -1.0 -7.0 2.1 NA Inf(v8 = as.logical(v7)) [1] TRUE FALSE TRUE FALSE TRUE TRUE TRUE TRUE TRUE NA TRUE# Convertir un vector numérico a un vector de factores
(v9 = c(1, 2, 2, 1, 3, 2))[1] 1 2 2 1 3 2(v10 = as.factor(v9))[1] 1 2 2 1 3 2
Levels: 1 2 3# Convertir un vector de caracteres a un vector de factores
(v11 = c("A", "B", "B", "A", "C", "B"))[1] "A" "B" "B" "A" "C" "B"(v12 = as.factor(v11))[1] A B B A C B
Levels: A B C13.4.1 Errores al convertir factor a numérico
Al convertir un vector de tipo factor con valores numéricos a vector numérico, se obtendrá un vector numérico con los niveles del factor.
Este primer ejemplo no presenta ningún problema en la conversión:
Sin embargo, en este otro ejemplo sí se producen errores al realizar la conversión, ya que aunque los niveles o “levels” asignados a las categorías del factor han sido: 1 2 7 9, al realizar la conversión a “numeric” serán reemplazados por los valores: 1 2 3 4, respectivamente, por lo que la conversión no será correcta.
Para solucionarlo, se puede convertir el factor a un vector de caracteres y luego a numérico.
(v15 = as.numeric(as.character(v13)))[1] 1 2 2 1 3 2(v16 = as.numeric(as.character(v13m)))[1] 1 2 9 1 7 213.5 Asignar nombres a los elementos de un objeto R
(v1 = 1:5)[1] 1 2 3 4 5(matriz1 = matrix(1:12, nrow = 3, ncol = 4)) [,1] [,2] [,3] [,4]
[1,] 1 4 7 10
[2,] 2 5 8 11
[3,] 3 6 9 12$a
[1] 1 2 3 4 5
$b
[1] "A" "B" "C"
$c
[,1] [,2] [,3] [,4]
[1,] 1 4 7 10
[2,] 2 5 8 11
[3,] 3 6 9 12(dataframe1 = data.frame(a = 1:5,
b = sample(c("A", "B", "C"), 5, replace = TRUE),
c = sample(c(T,F), 5, replace = TRUE)
)) a b c
1 1 B FALSE
2 2 A TRUE
3 3 C TRUE
4 4 C FALSE
5 5 A FALSE13.6 Escribir código más eficiente en R
Para ejecutar código más rápido, evidentemente, lo mejor es tener un mejor equipo: procesador más rápido y mayor número de núcleos, más memoria RAM, etc.
Como regla general, es más importante escribir código fácil de mantener y entendible que optimizar su velocidad. Pero cuando se trabaja con grandes conjuntos de datos o tareas altamente repetitivas, la velocidad puede ser mejor.
-
Varias técnicas de codificación puede ayudarte a hacer programas más eficientes:
- Leer solamente los datos que necesitamos.
- Usar vectorización más que bucles cuando sea posible.
- Crear objetos del tamaño correcto, más que cambiar el tamaño varias veces.
- Usar paralelización para tareas repetitivas e independientes.
Vectorización significa que usemos funciones R que estén diseñadas para procesar vectores de una manera más eficiente.
En el paquete base existen ejemplos como:
ifelse(),colSums(),colMeans(),rowSums(),rowMeans().El paquete matrixStats ofrece funciones optimizadas para muchos cálculos adicionales: conteos, sumas, productos, medidas de tendencia central y dispersión, cuantiles, rangos.
Paquetes como: plyr, dplyr, reshape2 y data.table también proveen funciones altamente optimizadas.
Ejemplo al considerar una matriz de 1 millón de filas y 10 columnas, y la función
colSums():
La función system.time() nos ayuda a determinar tiempos de CPU:
system.time(acumula(mimatrix)) # elapsed: 25.75
system.time(colSums(mimatrix)) # elapsed: 0.02 (1200 más rápida)- Es más eficiente iniciar objetos con su tamaño requerido final e ir rellenándolo, que comenzar con un objeto de tamaño pequeño e ir aumentándolo a medida que se requiere.
- Aproximación 1:
y = 0
system.time(for (i in 1:length(x)) y[i] = x[i]^2) # elapsed: 10.03- Aproximación 2:
y = numeric(length=k)
system.time(for (i in 1:length(x)) y[i] = x[i]^2) # elapsed: 0.24- Aproximación 3 (vectorización):
y = numeric(length=k)
system.time(y = x^2) # elapsed: 0- Nota: Las operaciones como exponenciación, suma, multiplicación, y parecidas son funciones vectorizadas.
Para grandes matrices la función rowMeans (se puede trasladar a funciones: ‘rowSums’, ‘colMeans’,…) es mucho más rápida que la función bucle ‘apply’.
myMA <- matrix(rnorm(1000000), 100000, 10, dimnames=list(1:100000, paste("C", 1:10, sep="")))
system.time(myMAmean <- apply(myMA, 1, mean))
# user system elapsed
# 0.969 0.025 1.002
system.time(myMAmean <- rowMeans(myMA))
# user system elapsed
# 0.005 0.001 0.006 14 Tratamiento de datos: Estudio Descriptivo
Se recomienda visitar el siguiente enlace que contiene una aplicación web para realizar una Exploración de datos cuantitativos: resúmenes estadísticos y gráficos (histogramas, boxplot, )
Se recuerda el contenido del data.frame “datos” que se ha utilizado en el ejemplo de la simulación de datos inicial:
str(datos)'data.frame': 100 obs. of 15 variables:
$ respuesta : num 194 308 344 247 303 ...
$ num_var1 : num -0.5605 -0.2302 1.5587 0.0705 0.1293 ...
$ num_var2 : num 61.9 98.1 80.1 75.8 70.1 ...
$ num_var3 : int 10 10 1 10 1 10 5 7 5 10 ...
$ num_var4 : int 1 2 5 4 4 1 1 7 3 3 ...
$ num_var5 : num 3.672 3.315 0.598 0.197 35 ...
$ num_var6 : int 0 0 1 1 1 1 0 0 0 0 ...
$ num_var7 : num 6.71 -16.51 -3.5 7.56 -5.39 ...
$ num_var8 : num -8.687 -1.189 -0.758 -3.181 -6.297 ...
$ factor_var1 : Factor w/ 2 levels "Categoría 1",..: 1 1 2 1 2 2 2 1 2 2 ...
$ factor_var2 : Factor w/ 3 levels "Grupo A","Grupo B",..: 1 1 3 3 1 1 3 2 2 3 ...
$ factor_var3 : Factor w/ 2 levels "Nivel 1","Nivel 2": 2 1 1 2 2 1 1 1 1 1 ...
$ factor_var4 : Factor w/ 4 levels "Tipo W","Tipo X",..: 4 4 4 2 2 1 4 4 2 4 ...
$ interaccion1: num -5.605 -2.302 1.559 0.705 0.129 ...
$ interaccion2: num 61.9 98.1 160.1 75.8 140.3 ...En los datos simulados de nuestro ejemplo se tienen diferentes tipos de variables:
-
Variables numéricas:
Variables discretas:
num_var3,num_var4,num_var6Variables continuas:
num_var1,num_var2,num_var5,num_var7,num_var8,interaccion1,interaccion2,respuesta
Variables cualitativas o categóricas:
factor_var1,factor_var2,factor_var3yfactor_var4
Desde el punto de vista de la regresión lineal, se consideran las siguientes variables:
respuesta <- 5 + 1.5 * num_var1 + 2 * num_var2 + 0.5 * num_var3 +
0.3 * num_var4 + 0.2 * num_var5 +
3 * as.numeric(factor_var1) + 2 * as.numeric(factor_var2) +
interaccion1 + interaccion2 + rnorm(nsim)Variable de respuesta u objetivo:
respuesta-
Variables predictoras o explicativas:
Variables explicativas reales:
num_var1,num_var2,num_var3,num_var4,num_var5,factor_var1,factor_var2,interaccion1,interaccion2Variables de interacción:
interaccion1,interaccion2Variables poco predictivas:
num_var7,num_var8
14.1 Tablas de frecuencia
# Tabla de frecuencia de la variable cualitativa factor_var2
(tabla_frecAbs_factor_var2 = table(factor_var2))factor_var2
Grupo A Grupo B Grupo C
30 35 35 (tabla_frecRel_factor_var2 = prop.table(tabla_frecAbs_factor_var2))factor_var2
Grupo A Grupo B Grupo C
0.30 0.35 0.35 Se puede presentar de una forma más compacta con un data.frame y cbind():
# Tabla de frecuencia de la variable cualitativa factor_var2
tabla_factor_var2 = data.frame(cbind(
FrecAbs = tabla_frecAbs_factor_var2,
FrecRel = tabla_frecRel_factor_var2,
Porc = tabla_frecRel_factor_var2 * 100))
tabla_factor_var2 FrecAbs FrecRel Porc
Grupo A 30 0.30 30
Grupo B 35 0.35 35
Grupo C 35 0.35 35# Tabla de frecuencia de la variable cuantitativa num_var3
(tabla_frecAbs_num_var3 = table(num_var3))num_var3
1 2 3 4 5 6 7 8 9 10
13 13 10 7 12 7 8 4 12 14 (tabla_frecRel_num_var3 = prop.table(tabla_frecAbs_num_var3))num_var3
1 2 3 4 5 6 7 8 9 10
0.13 0.13 0.10 0.07 0.12 0.07 0.08 0.04 0.12 0.14 (tabla_frecAbsAcum_num_var3 = cumsum(tabla_frecAbs_num_var3)) 1 2 3 4 5 6 7 8 9 10
13 26 36 43 55 62 70 74 86 100 (tabla_frecRelAcum_num_var3 = cumsum(tabla_frecRel_num_var3)) 1 2 3 4 5 6 7 8 9 10
0.13 0.26 0.36 0.43 0.55 0.62 0.70 0.74 0.86 1.00 Se puede presentar de una forma más compacta con un data.frame y cbind():
# Tabla de frecuencia de la variable cuantitativa num_var3
tabla_num_var3 = data.frame(cbind(
FrecAbs = tabla_frecAbs_num_var3,
FrecRel = tabla_frecRel_num_var3,
FrecAbsAcum = tabla_frecAbsAcum_num_var3,
FrecRelAcum = tabla_frecRelAcum_num_var3))
tabla_num_var3 FrecAbs FrecRel FrecAbsAcum FrecRelAcum
1 13 0.13 13 0.13
2 13 0.13 26 0.26
3 10 0.10 36 0.36
4 7 0.07 43 0.43
5 12 0.12 55 0.55
6 7 0.07 62 0.62
7 8 0.08 70 0.70
8 4 0.04 74 0.74
9 12 0.12 86 0.86
10 14 0.14 100 1.00# Tabla de frecuencia de la variable cuantitativa num_var1
AgrupaenIntervalos = cut(num_var1, breaks = 5)
(tabla_frecAbs_num_var1 = table(AgrupaenIntervalos))AgrupaenIntervalos
(-2.31,-1.41] (-1.41,-0.511] (-0.511,0.389] (0.389,1.29] (1.29,2.19]
4 20 40 26 10 (tabla_frecRel_num_var1 = prop.table(tabla_frecAbs_num_var1))AgrupaenIntervalos
(-2.31,-1.41] (-1.41,-0.511] (-0.511,0.389] (0.389,1.29] (1.29,2.19]
0.04 0.20 0.40 0.26 0.10 (tabla_frecAbsAcum_num_var1 = cumsum(tabla_frecAbs_num_var1)) (-2.31,-1.41] (-1.41,-0.511] (-0.511,0.389] (0.389,1.29] (1.29,2.19]
4 24 64 90 100 (tabla_frecRelAcum_num_var1 = cumsum(tabla_frecRel_num_var1)) (-2.31,-1.41] (-1.41,-0.511] (-0.511,0.389] (0.389,1.29] (1.29,2.19]
0.04 0.24 0.64 0.90 1.00 Se puede presentar de una forma más compacta con un data.frame y cbind():
# Tabla de frecuencia de la variable cuantitativa num_var1
tabla_num_var1 = data.frame(cbind(
FrecAbs = tabla_frecAbs_num_var1,
FrecRel = tabla_frecRel_num_var1,
Porc = tabla_frecRel_num_var1 * 100,
FrecAbsAcum = tabla_frecAbsAcum_num_var1,
FrecRelAcum = tabla_frecRelAcum_num_var1,
PorcAcum = tabla_frecRelAcum_num_var1 * 100
))
tabla_num_var1 FrecAbs FrecRel Porc FrecAbsAcum FrecRelAcum PorcAcum
(-2.31,-1.41] 4 0.04 4 4 0.04 4
(-1.41,-0.511] 20 0.20 20 24 0.24 24
(-0.511,0.389] 40 0.40 40 64 0.64 64
(0.389,1.29] 26 0.26 26 90 0.90 90
(1.29,2.19] 10 0.10 10 100 1.00 100# En este ejemplo no todos los intervalos tienen la misma amplitud
# Se recomienda incluir las marcas de clase y la amplitud de los intervalos
ExtIntervalos = c(-2.5,-1.5,-0.5, 0, 0.5,1.5,2.5)
AgrupaenIntervalos = cut(num_var1, breaks = ExtIntervalos,
right = FALSE, include.lowest = TRUE)
(tabla_frecAbs_num_var1 = table(AgrupaenIntervalos))AgrupaenIntervalos
[-2.5,-1.5) [-1.5,-0.5) [-0.5,0) [0,0.5) [0.5,1.5) [1.5,2.5]
4 21 23 22 22 8 (tabla_frecRel_num_var1 = prop.table(tabla_frecAbs_num_var1))AgrupaenIntervalos
[-2.5,-1.5) [-1.5,-0.5) [-0.5,0) [0,0.5) [0.5,1.5) [1.5,2.5]
0.04 0.21 0.23 0.22 0.22 0.08 (tabla_frecAbsAcum_num_var1 = cumsum(tabla_frecAbs_num_var1))[-2.5,-1.5) [-1.5,-0.5) [-0.5,0) [0,0.5) [0.5,1.5) [1.5,2.5]
4 25 48 70 92 100 (tabla_frecRelAcum_num_var1 = cumsum(tabla_frecRel_num_var1))[-2.5,-1.5) [-1.5,-0.5) [-0.5,0) [0,0.5) [0.5,1.5) [1.5,2.5]
0.04 0.25 0.48 0.70 0.92 1.00 De modo más compacto con un data.frame y cbind():
# Tabla de frecuencia de la variable cuantitativa num_var1
tabla_num_var1 = data.frame(cbind(
FrecAbs = tabla_frecAbs_num_var1,
FrecRel = tabla_frecRel_num_var1,
Porc = tabla_frecRel_num_var1 * 100,
FrecAbsAcum = tabla_frecAbsAcum_num_var1,
FrecRelAcum = tabla_frecRelAcum_num_var1,
PorcAcum = tabla_frecRelAcum_num_var1 * 100,
MarcasClase = as.numeric(
(ExtIntervalos[1:(length(ExtIntervalos) - 1)] +
ExtIntervalos[2:length(ExtIntervalos)]) / 2),
Amplitud = diff(ExtIntervalos)
))
tabla_num_var1 FrecAbs FrecRel Porc FrecAbsAcum FrecRelAcum PorcAcum MarcasClase Amplitud
[-2.5,-1.5) 4 0.04 4 4 0.04 4 -2.00 1.0
[-1.5,-0.5) 21 0.21 21 25 0.25 25 -1.00 1.0
[-0.5,0) 23 0.23 23 48 0.48 48 -0.25 0.5
[0,0.5) 22 0.22 22 70 0.70 70 0.25 0.5
[0.5,1.5) 22 0.22 22 92 0.92 92 1.00 1.0
[1.5,2.5] 8 0.08 8 100 1.00 100 2.00 1.0Añadimos a la tabla básica la amplitud de los intervalos y los extremos de los intervalos, con ayuda de la función definida en Sección 12.4.1: Extremos_IntervalosAgrup().
(ExtIntervalos = Extremos_IntervalosAgrup(num_var1, breaks_ = 5))[1] -2.310 -1.410 -0.511 0.389 1.290 2.190Se puede presentar de una forma más compacta con un data.frame y cbind():
# Tabla de frecuencia de la variable cuantitativa num_var1
tablaComp_num_var1 = data.frame(cbind(
FrecAbs = tabla_frecAbs_num_var1,
FrecRel = tabla_frecRel_num_var1,
Porc = tabla_frecRel_num_var1 * 100,
FrecAbsAcum = tabla_frecAbsAcum_num_var1,
FrecRelAcum = tabla_frecRelAcum_num_var1,
PorcAcum = tabla_frecRelAcum_num_var1 * 100,
MarcasClase = as.numeric(
(ExtIntervalos[1:(length(ExtIntervalos) - 1)] +
ExtIntervalos[2:length(ExtIntervalos)]) / 2),
Amplitud = diff(ExtIntervalos)
))
tablaComp_num_var1 FrecAbs FrecRel Porc FrecAbsAcum FrecRelAcum PorcAcum MarcasClase Amplitud
[-2.5,-1.5) 4 0.04 4 4 0.04 4 -1.8600 0.900
[-1.5,-0.5) 21 0.21 21 25 0.25 25 -0.9605 0.899
[-0.5,0) 23 0.23 23 48 0.48 48 -0.0610 0.900
[0,0.5) 22 0.22 22 70 0.70 70 0.8395 0.901
[0.5,1.5) 22 0.22 22 92 0.92 92 1.7400 0.900
[1.5,2.5] 8 0.08 8 100 1.00 100 -1.8600 0.90014.2 Tablas multidimensionales o de contingencia
# Tabla de contingencia de las variables cualitativas factor_var1 y factor_var2
(tabla_contingencia = table(factor_var1, factor_var2)) factor_var2
factor_var1 Grupo A Grupo B Grupo C
Categoría 1 16 20 14
Categoría 2 14 15 21# Tabla de contingencia de las variables cualitativas factor_var1 y factor_var2
(tabla_contingencia = prop.table(table(factor_var1, factor_var2))) factor_var2
factor_var1 Grupo A Grupo B Grupo C
Categoría 1 0.16 0.20 0.14
Categoría 2 0.14 0.15 0.21# Tabla de contingencia de las variables cualitativas factor_var1 y factor_var2
(tabla_contingencia = prop.table(table(factor_var1, factor_var2)) * 100) factor_var2
factor_var1 Grupo A Grupo B Grupo C
Categoría 1 16 20 14
Categoría 2 14 15 21# Frecuencias condicionadas de la variable factor_var1 por la variable factor_var2
(tabla_contingencia = prop.table(table(factor_var1, factor_var2), margin = 2)) factor_var2
factor_var1 Grupo A Grupo B Grupo C
Categoría 1 0.5333333 0.5714286 0.4000000
Categoría 2 0.4666667 0.4285714 0.6000000# Frecuencias condicionadas de la variable factor_var2 por la variable factor_var1
(tabla_contingencia = prop.table(table(factor_var1, factor_var2), margin = 1)) factor_var2
factor_var1 Grupo A Grupo B Grupo C
Categoría 1 0.32 0.40 0.28
Categoría 2 0.28 0.30 0.42# Tabla de contingencia de las variables cualitativas factor_var1, factor_var2 y factor_var3
(tabla_contingencia = table(factor_var1, factor_var2, factor_var3)), , factor_var3 = Nivel 1
factor_var2
factor_var1 Grupo A Grupo B Grupo C
Categoría 1 7 13 6
Categoría 2 5 13 12
, , factor_var3 = Nivel 2
factor_var2
factor_var1 Grupo A Grupo B Grupo C
Categoría 1 9 7 8
Categoría 2 9 2 9# Tabla de contingencia de las variables cualitativas factor_var1 y factor_var2
(ftable(factor_var1, factor_var2, factor_var3)) factor_var3 Nivel 1 Nivel 2
factor_var1 factor_var2
Categoría 1 Grupo A 7 9
Grupo B 13 7
Grupo C 6 8
Categoría 2 Grupo A 5 9
Grupo B 13 2
Grupo C 12 914.3 Estadísticos descriptivos
14.3.1 Para variables unididimensionales
Ya se han visto en el apartado Sección 11.3.4, muchas de las funciones que tiene R para realizar cálculos estadísticos básicos: sum(), mean(), median(), var(), sd(), min(), max(), range(), quantile(), IQR(), fBasics::skewness(), fBasics::kurtosis().
Las siguientes funciones nos permiten obtener un resumen de los estadísticos descriptivos de una variable.
# Estadísticos descriptivos de la variable num_var1
summary(num_var1) Min. 1st Qu. Median Mean 3rd Qu. Max.
-2.30917 -0.49385 0.06176 0.09041 0.69182 2.18733 # Estadísticos descriptivos de la variable factor_var2
summary(factor_var2)Grupo A Grupo B Grupo C
30 35 35 # Estadísticos descriptivos de cada columna de un data.frame
summary(datos) respuesta num_var1 num_var2 num_var3 num_var4 num_var5 num_var6
Min. :156.0 Min. :-2.30917 Min. :50.32 Min. : 1.00 Min. :0.00 Min. : 0.05817 Min. :0.00
1st Qu.:235.5 1st Qu.:-0.49385 1st Qu.:61.28 1st Qu.: 2.00 1st Qu.:2.00 1st Qu.: 2.31220 1st Qu.:0.00
Median :285.3 Median : 0.06176 Median :73.74 Median : 5.00 Median :3.00 Median : 6.18999 Median :0.00
Mean :280.4 Mean : 0.09041 Mean :74.30 Mean : 5.35 Mean :2.99 Mean : 9.46029 Mean :0.45
3rd Qu.:320.2 3rd Qu.: 0.69182 3rd Qu.:86.50 3rd Qu.: 9.00 3rd Qu.:4.00 3rd Qu.:12.60971 3rd Qu.:1.00
Max. :422.5 Max. : 2.18733 Max. :99.11 Max. :10.00 Max. :8.00 Max. :39.46983 Max. :1.00
num_var7 num_var8 factor_var1 factor_var2 factor_var3 factor_var4 interaccion1
Min. :-26.609 Min. :-9.7378 Categoría 1:50 Grupo A:30 Nivel 1:56 Tipo W:27 Min. :-16.1642
1st Qu.: -3.964 1st Qu.:-4.4940 Categoría 2:50 Grupo B:35 Nivel 2:44 Tipo X:28 1st Qu.: -2.0421
Median : 2.046 Median :-0.1288 Grupo C:35 Tipo Y:23 Median : 0.1176
Mean : 1.267 Mean :-0.1882 Tipo Z:22 Mean : 0.6168
3rd Qu.: 7.524 3rd Qu.: 4.4315 3rd Qu.: 3.2780
Max. : 23.975 Max. : 9.8523 Max. : 17.4987
interaccion2
Min. : 50.32
1st Qu.: 73.04
Median :100.55
Mean :111.96
3rd Qu.:147.89
Max. :196.94 vars n mean sd median trimmed mad min max range skew kurtosis se
respuesta 1 100 280.38 67.16 285.26 278.41 70.76 155.95 422.55 266.60 0.14 -0.78 6.72
num_var1 2 100 0.09 0.91 0.06 0.08 0.89 -2.31 2.19 4.50 0.06 -0.22 0.09
num_var2 3 100 74.30 14.72 73.74 74.11 18.71 50.32 99.11 48.79 0.08 -1.28 1.47
num_var3 4 100 5.35 3.14 5.00 5.31 4.45 1.00 10.00 9.00 0.13 -1.40 0.31
num_var4 5 100 2.99 1.77 3.00 2.88 1.48 0.00 8.00 8.00 0.55 0.03 0.18
num_var5 6 100 9.46 9.82 6.19 7.68 7.15 0.06 39.47 39.41 1.47 1.48 0.98
num_var6 7 100 0.45 0.50 0.00 0.44 0.00 0.00 1.00 1.00 0.20 -1.98 0.05
num_var7 8 100 1.27 9.93 2.05 1.74 8.60 -26.61 23.97 50.58 -0.46 0.23 0.99
num_var8 9 100 -0.19 5.29 -0.13 -0.16 6.59 -9.74 9.85 19.59 -0.03 -1.07 0.53
factor_var1* 10 100 1.50 0.50 1.50 1.50 0.74 1.00 2.00 1.00 0.00 -2.02 0.05
factor_var2* 11 100 2.05 0.81 2.00 2.06 1.48 1.00 3.00 2.00 -0.09 -1.48 0.08
factor_var3* 12 100 1.44 0.50 1.00 1.43 0.00 1.00 2.00 1.00 0.24 -1.96 0.05
factor_var4* 13 100 2.40 1.11 2.00 2.38 1.48 1.00 4.00 3.00 0.14 -1.34 0.11
interaccion1 14 100 0.62 5.71 0.12 0.55 4.06 -16.16 17.50 33.66 0.19 1.23 0.57
interaccion2 15 100 111.96 44.50 100.55 109.78 57.92 50.32 196.94 146.62 0.28 -1.23 4.45datos
15 Variables 100 Observations
------------------------------------------------------------------------------------------------------------------------
respuesta
n missing distinct Info Mean Gmd .05 .10 .25 .50 .75 .90 .95
100 0 100 1 280.4 77.07 176.6 187.1 235.5 285.3 320.2 377.3 394.5
lowest : 155.9509 168.5110 170.7268 171.3548 174.5528, highest: 405.9259 409.4319 410.1735 416.7474 422.5490
------------------------------------------------------------------------------------------------------------------------
num_var1
n missing distinct Info Mean Gmd .05 .10 .25 .50 .75 .90 .95
100 0 100 1 0.09041 1.036 -1.26508 -1.06822 -0.49385 0.06176 0.69182 1.26450 1.56653
lowest : -2.309169 -1.966617 -1.686693 -1.548753 -1.265396, highest: 1.715065 1.786913 2.050085 2.168956 2.187333
------------------------------------------------------------------------------------------------------------------------
num_var2
n missing distinct Info Mean Gmd .05 .10 .25 .50 .75 .90 .95
100 0 100 1 74.3 17.06 52.89 53.71 61.28 73.74 86.50 94.27 98.06
lowest : 50.31504 51.00122 52.38318 52.64220 52.73146, highest: 98.11795 98.36992 98.46782 98.59378 99.10702
------------------------------------------------------------------------------------------------------------------------
num_var3
n missing distinct Info Mean Gmd .05 .10 .25 .50 .75 .90 .95
100 0 10 0.987 5.35 3.61 1 1 2 5 9 10 10
lowest : 1 2 3 4 5, highest: 6 7 8 9 10
Value 1 2 3 4 5 6 7 8 9 10
Frequency 13 13 10 7 12 7 8 4 12 14
Proportion 0.13 0.13 0.10 0.07 0.12 0.07 0.08 0.04 0.12 0.14
------------------------------------------------------------------------------------------------------------------------
num_var4
n missing distinct Info Mean Gmd
100 0 9 0.966 2.99 1.963
lowest : 0 1 2 3 4, highest: 4 5 6 7 8
Value 0 1 2 3 4 5 6 7 8
Frequency 5 16 24 16 22 9 4 2 2
Proportion 0.05 0.16 0.24 0.16 0.22 0.09 0.04 0.02 0.02
------------------------------------------------------------------------------------------------------------------------
num_var5
n missing distinct Info Mean Gmd .05 .10 .25 .50 .75 .90 .95
100 0 100 1 9.46 10.1 0.3866 0.6110 2.3122 6.1900 12.6097 24.4694 33.0934
lowest : 0.05816608 0.16741259 0.19685799 0.22161044 0.30600416
highest: 35.00006681 36.41037261 37.50472491 38.73333683 39.46983402
------------------------------------------------------------------------------------------------------------------------
num_var6
n missing distinct Info Sum Mean Gmd
100 0 2 0.743 45 0.45 0.5
------------------------------------------------------------------------------------------------------------------------
num_var7
n missing distinct Info Mean Gmd .05 .10 .25 .50 .75 .90 .95
100 0 100 1 1.267 11.12 -16.371 -11.076 -3.964 2.046 7.524 12.975 16.375
lowest : -26.60923 -26.43149 -22.24988 -20.52337 -16.50547, highest: 17.12305 17.24262 17.79503 19.75419 23.97452
------------------------------------------------------------------------------------------------------------------------
num_var8
n missing distinct Info Mean Gmd .05 .10 .25 .50 .75 .90 .95
100 0 100 1 -0.1882 6.128 -8.4930 -7.4393 -4.4940 -0.1288 4.4315 6.5475 7.5747
lowest : -9.737836 -9.616179 -9.413268 -9.401203 -8.687438, highest: 7.837925 8.752647 9.483274 9.849106 9.852313
------------------------------------------------------------------------------------------------------------------------
factor_var1
n missing distinct
100 0 2
Value Categoría 1 Categoría 2
Frequency 50 50
Proportion 0.5 0.5
------------------------------------------------------------------------------------------------------------------------
factor_var2
n missing distinct
100 0 3
Value Grupo A Grupo B Grupo C
Frequency 30 35 35
Proportion 0.30 0.35 0.35
------------------------------------------------------------------------------------------------------------------------
factor_var3
n missing distinct
100 0 2
Value Nivel 1 Nivel 2
Frequency 56 44
Proportion 0.56 0.44
------------------------------------------------------------------------------------------------------------------------
factor_var4
n missing distinct
100 0 4
Value Tipo W Tipo X Tipo Y Tipo Z
Frequency 27 28 23 22
Proportion 0.27 0.28 0.23 0.22
------------------------------------------------------------------------------------------------------------------------
interaccion1
n missing distinct Info Mean Gmd .05 .10 .25 .50 .75 .90 .95
100 0 100 1 0.6168 6.176 -8.8555 -5.6445 -2.0421 0.1176 3.2780 8.2151 9.0926
lowest : -16.164182 -13.938775 -10.986459 -9.105095 -8.857774, highest: 9.871551 11.016736 15.326106 17.150650 17.498664
------------------------------------------------------------------------------------------------------------------------
interaccion2
n missing distinct Info Mean Gmd .05 .10 .25 .50 .75 .90 .95
100 0 100 1 112 51.2 53.23 56.69 73.04 100.55 147.89 175.74 188.05
lowest : 50.31504 52.38318 52.64220 52.73146 52.89793, highest: 188.19776 191.56835 192.57080 195.01670 196.93564
------------------------------------------------------------------------------------------------------------------------Con el sistema tidyverse se pueden realizar cálculos agrupados de forma sencilla con la función dplyr::group_by() y dplyr::summarise() (ver: Sección 11.5).
# Medias de la variable num_var1 para cada nivel de factor_var1
aggregate(num_var1,
by = list(factor_var1),
FUN = mean) Group.1 x
1 Categoría 1 -0.0347612
2 Categoría 2 0.2155730# Cuasivarianzas de num_var1 para cada nivel de factor_var1 y factor_var2
aggregate(num_var1,
by = list(factor_var1, factor_var2),
FUN = var) Group.1 Group.2 x
1 Categoría 1 Grupo A 0.6061448
2 Categoría 2 Grupo A 0.7189208
3 Categoría 1 Grupo B 1.0268887
4 Categoría 2 Grupo B 0.9523861
5 Categoría 1 Grupo C 0.8783549
6 Categoría 2 Grupo C 0.6866582# Media de las variables numéricas para cada nivel de factor_var1 y factor_var2
aggregate(datos[, sapply(datos, is.numeric)],
by = list(factor_var1, factor_var2),
FUN = mean) Group.1 Group.2 respuesta num_var1 num_var2 num_var3 num_var4 num_var5 num_var6 num_var7 num_var8
1 Categoría 1 Grupo A 242.8964 -0.141015909 76.49134 5.125000 3.125000 7.489144 0.4375000 -2.875365 0.6515100
2 Categoría 2 Grupo A 334.9341 -0.075670707 78.69544 5.714286 3.000000 14.251773 0.6428571 -0.503235 -1.0768854
3 Categoría 1 Grupo B 238.7716 -0.003877907 73.80915 5.200000 3.000000 10.044609 0.3000000 5.071061 -0.9397754
4 Categoría 2 Grupo B 310.1744 0.013530797 72.53029 4.333333 2.733333 8.827938 0.4666667 1.558241 -0.4083568
5 Categoría 1 Grupo C 227.3626 0.042553771 68.86610 6.714286 3.214286 7.471806 0.5000000 -1.213678 0.5575380
6 Categoría 2 Grupo C 326.2458 0.554051366 75.06657 5.238095 2.904762 8.988659 0.4285714 3.427582 0.1404752
interaccion1 interaccion2
1 -1.21858891 76.49134
2 0.35978587 157.39087
3 0.02954511 73.80915
4 0.47470769 145.06058
5 0.81727113 68.86610
6 2.71373021 150.13315library(psych)
describeBy(datos, group = list(factor_var1) )
Descriptive statistics by group
: Categoría 1
vars n mean sd median trimmed mad min max range skew kurtosis se
respuesta 1 50 236.90 49.58 234.43 235.73 67.73 155.95 340.73 184.78 0.18 -1.36 7.01
num_var1 2 50 -0.03 0.91 -0.12 -0.05 0.83 -2.31 2.19 4.50 0.11 -0.19 0.13
num_var2 3 50 73.28 16.26 72.50 72.77 21.16 50.32 99.11 48.79 0.16 -1.53 2.30
num_var3 4 50 5.60 3.38 6.00 5.62 4.45 1.00 10.00 9.00 -0.06 -1.61 0.48
num_var4 5 50 3.10 1.98 3.00 3.00 1.48 0.00 8.00 8.00 0.45 -0.18 0.28
num_var5 6 50 8.51 9.05 6.42 6.83 7.40 0.17 39.47 39.30 1.76 3.05 1.28
num_var6 7 50 0.40 0.49 0.00 0.38 0.00 0.00 1.00 1.00 0.40 -1.88 0.07
num_var7 8 50 0.77 10.47 2.06 1.32 8.12 -26.61 23.97 50.58 -0.47 0.14 1.48
num_var8 9 50 -0.01 4.82 -0.82 -0.05 5.06 -8.69 9.85 18.54 0.11 -0.91 0.68
factor_var1* 10 50 1.00 0.00 1.00 1.00 0.00 1.00 1.00 0.00 NaN NaN 0.00
factor_var2* 11 50 1.96 0.78 2.00 1.95 1.48 1.00 3.00 2.00 0.07 -1.39 0.11
factor_var3* 12 50 1.48 0.50 1.00 1.48 0.00 1.00 2.00 1.00 0.08 -2.03 0.07
factor_var4* 13 50 2.60 1.11 3.00 2.62 1.48 1.00 4.00 3.00 -0.07 -1.38 0.16
interaccion1 14 50 -0.15 6.17 -0.12 -0.28 3.76 -16.16 17.50 33.66 0.22 1.25 0.87
interaccion2 15 50 73.28 16.26 72.50 72.77 21.16 50.32 99.11 48.79 0.16 -1.53 2.30
------------------------------------------------------------------------------------------
: Categoría 2
vars n mean sd median trimmed mad min max range skew kurtosis se
respuesta 1 50 323.86 52.88 317.77 322.97 54.90 236.96 422.55 185.59 0.13 -1.07 7.48
num_var1 2 50 0.22 0.91 0.16 0.22 0.81 -1.97 2.17 4.14 0.01 -0.31 0.13
num_var2 3 50 75.32 13.08 74.00 75.34 14.25 51.00 98.47 47.47 0.04 -1.02 1.85
num_var3 4 50 5.10 2.89 5.00 5.00 2.97 1.00 10.00 9.00 0.34 -1.11 0.41
num_var4 5 50 2.88 1.53 3.00 2.75 1.48 1.00 7.00 6.00 0.56 -0.40 0.22
num_var5 6 50 10.41 10.54 6.13 8.74 7.13 0.06 38.73 38.68 1.19 0.36 1.49
num_var6 7 50 0.50 0.51 0.50 0.50 0.74 0.00 1.00 1.00 0.00 -2.04 0.07
num_var7 8 50 1.77 9.43 1.96 2.08 9.57 -26.43 19.75 46.19 -0.40 0.07 1.33
num_var8 9 50 -0.37 5.78 0.77 -0.32 7.77 -9.74 9.85 19.59 -0.08 -1.31 0.82
factor_var1* 10 50 2.00 0.00 2.00 2.00 0.00 2.00 2.00 0.00 NaN NaN 0.00
factor_var2* 11 50 2.14 0.83 2.00 2.17 1.48 1.00 3.00 2.00 -0.26 -1.54 0.12
factor_var3* 12 50 1.40 0.49 1.00 1.38 0.00 1.00 2.00 1.00 0.40 -1.88 0.07
factor_var4* 13 50 2.20 1.09 2.00 2.12 1.48 1.00 4.00 3.00 0.35 -1.23 0.15
interaccion1 14 50 1.38 5.16 0.61 1.30 4.30 -10.99 17.15 28.14 0.33 0.71 0.73
interaccion2 15 50 150.64 26.15 147.99 150.69 28.51 102.00 196.94 94.93 0.04 -1.02 3.70# En forma de matriz
describeBy(datos, group = list(factor_var1), mat = TRUE) item group1 vars n mean sd median trimmed mad min
respuesta1 1 Categoría 1 1 50 236.89702713 49.5802694 234.4321447 235.72875578 67.7348058 155.95091381
respuesta2 2 Categoría 2 1 50 323.85709637 52.8758127 317.7725022 322.97284666 54.8978185 236.96030528
num_var11 3 Categoría 1 2 50 -0.03476120 0.9069468 -0.1232608 -0.05058004 0.8326208 -2.30916888
num_var12 4 Categoría 2 2 50 0.21557301 0.9104641 0.1552956 0.21834402 0.8109429 -1.96661716
num_var21 5 Categoría 1 3 50 73.28339867 16.2624759 72.4999447 72.77390567 21.1631172 50.31503920
num_var22 6 Categoría 2 3 50 75.32177035 13.0762868 73.9971996 75.34257693 14.2544909 51.00121503
num_var31 7 Categoría 1 4 50 5.60000000 3.3806170 6.0000000 5.62500000 4.4478000 1.00000000
num_var32 8 Categoría 2 4 50 5.10000000 2.8943999 5.0000000 5.00000000 2.9652000 1.00000000
num_var41 9 Categoría 1 5 50 3.10000000 1.9820624 3.0000000 3.00000000 1.4826000 0.00000000
num_var42 10 Categoría 2 5 50 2.88000000 1.5338361 3.0000000 2.75000000 1.4826000 1.00000000
num_var51 11 Categoría 1 6 50 8.50647523 9.0534741 6.4167277 6.82867312 7.4031391 0.16741259
num_var52 12 Categoría 2 6 50 10.41411437 10.5360180 6.1312959 8.74346510 7.1302541 0.05816608
num_var61 13 Categoría 1 7 50 0.40000000 0.4948717 0.0000000 0.37500000 0.0000000 0.00000000
num_var62 14 Categoría 2 7 50 0.50000000 0.5050763 0.5000000 0.50000000 0.7413000 0.00000000
num_var71 15 Categoría 1 8 50 0.76847779 10.4738369 2.0623201 1.32332622 8.1172626 -26.60922798
num_var72 16 Categoría 2 8 50 1.76615115 9.4336356 1.9630647 2.08284824 9.5722368 -26.43148952
num_var81 17 Categoría 1 9 50 -0.01131633 4.8156221 -0.8189667 -0.04700995 5.0578456 -8.68743776
num_var82 18 Categoría 2 9 50 -0.36503538 5.7783994 0.7657785 -0.32062983 7.7693650 -9.73783568
factor_var1*1 19 Categoría 1 10 50 1.00000000 0.0000000 1.0000000 1.00000000 0.0000000 1.00000000
factor_var1*2 20 Categoría 2 10 50 2.00000000 0.0000000 2.0000000 2.00000000 0.0000000 2.00000000
factor_var2*1 21 Categoría 1 11 50 1.96000000 0.7814168 2.0000000 1.95000000 1.4826000 1.00000000
factor_var2*2 22 Categoría 2 11 50 2.14000000 0.8332381 2.0000000 2.17500000 1.4826000 1.00000000
factor_var3*1 23 Categoría 1 12 50 1.48000000 0.5046720 1.0000000 1.47500000 0.0000000 1.00000000
factor_var3*2 24 Categoría 2 12 50 1.40000000 0.4948717 1.0000000 1.37500000 0.0000000 1.00000000
factor_var4*1 25 Categoría 1 13 50 2.60000000 1.1065667 3.0000000 2.62500000 1.4826000 1.00000000
factor_var4*2 26 Categoría 2 13 50 2.20000000 1.0879676 2.0000000 2.12500000 1.4826000 1.00000000
interaccion11 27 Categoría 1 14 50 -0.14929449 6.1667048 -0.1245167 -0.28065006 3.7580841 -16.16418213
interaccion12 28 Categoría 2 14 50 1.38291904 5.1590805 0.6083557 1.30113432 4.3020800 -10.98645941
interaccion21 29 Categoría 1 15 50 73.28339867 16.2624759 72.4999447 72.77390567 21.1631172 50.31503920
interaccion22 30 Categoría 2 15 50 150.64354069 26.1525736 147.9943993 150.68515387 28.5089819 102.00243006
max range skew kurtosis se
respuesta1 340.734459 184.783545 0.180973264 -1.35640515 7.01170894
respuesta2 422.549036 185.588731 0.130412026 -1.06502301 7.47776914
num_var11 2.187333 4.496502 0.110977015 -0.19261673 0.12826165
num_var12 2.168956 4.135573 0.007301933 -0.30743790 0.12875906
num_var21 99.107019 48.791979 0.156933398 -1.52660906 2.29986140
num_var22 98.467821 47.466606 0.044129741 -1.01951689 1.84926621
num_var31 10.000000 9.000000 -0.064603591 -1.60756700 0.47809144
num_var32 10.000000 9.000000 0.338007493 -1.11053649 0.40932997
num_var41 8.000000 8.000000 0.449999589 -0.18101461 0.28030596
num_var42 7.000000 6.000000 0.563030801 -0.40273042 0.21691718
num_var51 39.469834 39.302421 1.756980310 3.04808243 1.28035459
num_var52 38.733337 38.675171 1.190608844 0.35645268 1.49001795
num_var61 1.000000 1.000000 0.396062285 -1.87953333 0.06998542
num_var62 1.000000 1.000000 0.000000000 -2.03960000 0.07142857
num_var71 23.974525 50.583753 -0.471921971 0.13682652 1.48122422
num_var72 19.754191 46.185680 -0.399663283 0.07210772 1.33411755
num_var81 9.849106 18.536544 0.107804242 -0.91372384 0.68103181
num_var82 9.852313 19.590149 -0.081518300 -1.30684768 0.81718908
factor_var1*1 1.000000 0.000000 NaN NaN 0.00000000
factor_var1*2 2.000000 0.000000 NaN NaN 0.00000000
factor_var2*1 3.000000 2.000000 0.066797630 -1.39249929 0.11050903
factor_var2*2 3.000000 2.000000 -0.256716748 -1.54207487 0.11783766
factor_var3*1 2.000000 1.000000 0.077674205 -2.03344359 0.07137141
factor_var3*2 2.000000 1.000000 0.396062285 -1.87953333 0.06998542
factor_var4*1 4.000000 3.000000 -0.070849775 -1.38012533 0.15649216
factor_var4*2 4.000000 3.000000 0.354092699 -1.23336647 0.15386185
interaccion11 17.498664 33.662846 0.221873674 1.25460673 0.87210375
interaccion12 17.150650 28.137109 0.326334248 0.70538109 0.72960416
interaccion21 99.107019 48.791979 0.156933398 -1.52660906 2.29986140
interaccion22 196.935641 94.933211 0.044129741 -1.01951689 3.6985324214.3.2 Para variables bidimensionales
# Correlación entre las variables num_var1 y num_var2
cor(num_var1, num_var2)[1] 0.05564807# Correlación entre todas las variables numéricas: `cor()`
round( cor(datos[, sapply(datos, is.numeric)]) , 4) respuesta num_var1 num_var2 num_var3 num_var4 num_var5 num_var6 num_var7 num_var8 interaccion1
respuesta 1.0000 0.2279 0.7852 -0.0502 -0.0285 0.1152 0.1485 0.0110 0.0994 0.2335
num_var1 0.2279 1.0000 0.0556 0.0469 -0.0820 0.2461 -0.1544 -0.2078 0.0508 0.8969
num_var2 0.7852 0.0556 1.0000 -0.0263 0.0112 0.0106 0.1177 -0.0109 0.1394 0.0475
num_var3 -0.0502 0.0469 -0.0263 1.0000 -0.0449 0.1313 -0.0113 -0.0276 -0.0085 0.0837
num_var4 -0.0285 -0.0820 0.0112 -0.0449 1.0000 0.0360 -0.1321 -0.0395 -0.0994 -0.1281
num_var5 0.1152 0.2461 0.0106 0.1313 0.0360 1.0000 -0.0896 -0.0116 0.0555 0.2963
num_var6 0.1485 -0.1544 0.1177 -0.0113 -0.1321 -0.0896 1.0000 0.1378 0.0857 -0.0892
num_var7 0.0110 -0.2078 -0.0109 -0.0276 -0.0395 -0.0116 0.1378 1.0000 0.1062 -0.1818
num_var8 0.0994 0.0508 0.1394 -0.0085 -0.0994 0.0555 0.0857 0.1062 1.0000 0.0852
interaccion1 0.2335 0.8969 0.0475 0.0837 -0.1281 0.2963 -0.0892 -0.1818 0.0852 1.0000
interaccion2 0.9260 0.1389 0.5191 -0.1086 -0.0428 0.0727 0.1677 0.0491 0.0458 0.1408
interaccion2
respuesta 0.9260
num_var1 0.1389
num_var2 0.5191
num_var3 -0.1086
num_var4 -0.0428
num_var5 0.0727
num_var6 0.1677
num_var7 0.0491
num_var8 0.0458
interaccion1 0.1408
interaccion2 1.0000# Covarianza entre las variables numéricas: `cov()`
round( cov(datos[, sapply(datos, is.numeric)]) , 4) respuesta num_var1 num_var2 num_var3 num_var4 num_var5 num_var6 num_var7 num_var8 interaccion1
respuesta 4510.1012 13.9691 776.0103 -10.5977 -3.3828 75.9442 4.9874 7.3344 35.3332 89.5362
num_var1 13.9691 0.8332 0.7476 0.1345 -0.1323 2.2057 -0.0705 -1.8838 0.2456 4.6737
num_var2 776.0103 0.7476 216.5787 -1.2168 0.2908 1.5301 0.8663 -1.5879 10.8656 3.9882
num_var3 -10.5977 0.1345 -1.2168 9.8662 -0.2490 4.0486 -0.0177 -0.8597 -0.1407 1.5006
num_var4 -3.3828 -0.1323 0.2908 -0.2490 3.1211 0.6244 -0.1167 -0.6930 -0.9302 -1.2922
num_var5 75.9442 2.2057 1.5301 4.0486 0.6244 96.4309 -0.4397 -1.1348 2.8843 16.6079
num_var6 4.9874 -0.0705 0.8663 -0.0177 -0.1167 -0.4397 0.2500 0.6842 0.2269 -0.2546
num_var7 7.3344 -1.8838 -1.5879 -0.8597 -0.6930 -1.1348 0.6842 98.5952 5.5819 -10.3033
num_var8 35.3332 0.2456 10.8656 -0.1407 -0.9302 2.8843 0.2269 5.5819 28.0359 2.5749
interaccion1 89.5362 4.6737 3.9882 1.5006 -1.2922 16.6079 -0.2546 -10.3033 2.5749 32.5885
interaccion2 2767.7710 5.6415 339.9809 -15.1841 -3.3624 31.7824 3.7319 21.6943 10.8014 35.7616
interaccion2
respuesta 2767.7710
num_var1 5.6415
num_var2 339.9809
num_var3 -15.1841
num_var4 -3.3624
num_var5 31.7824
num_var6 3.7319
num_var7 21.6943
num_var8 10.8014
interaccion1 35.7616
interaccion2 1980.683114.4 Gráficos con el sistema base
14.4.1 Gráficos de barras
bp01 = barplot(table(factor_var2), col = "lightblue",
border="orange",space=0.1,
main = "Gráfico de barras de factor_var2",
xlab = "Niveles de factor_var2",
cex.names = 0.8,
xaxt = "n")
text(bp01, 0, labels = names(table(factor_var2)),
srt = 45, adj = c(1.1,1.1), # pos = 2,
xpd = TRUE)
# Añade texto a las barras
text(x = bp01, y = table(factor_var2), label = table(factor_var2),
pos = 1, cex = 0.9, col = "red")tbfactor_var2 = table(factor_var2)
tbfactor_var2ord = tbfactor_var2[order(tbfactor_var2, decreasing = TRUE)]
bp01 = barplot(tbfactor_var2ord, col = "lightblue",
border="orange",space=0.1,
main = "Gráfico de barras de factor_var2",
xlab = "Niveles de factor_var2",
cex.names = 0.8,
xaxt = "n")
text(bp01, 0, labels = names(tbfactor_var2ord),
srt = 45, adj = c(1.1,1.1), # pos = 2,
xpd = TRUE)
# Añade texto a las barras
text(x = bp01, y = tbfactor_var2ord, label = tbfactor_var2ord,
pos = 1, cex = 0.9, col = "red")tbfactor_var2 = prop.table(table(factor_var2)) * 100
tbfactor_var2ord = tbfactor_var2[order(tbfactor_var2, decreasing = TRUE)]
bp01 = barplot(tbfactor_var2ord, col = "lightblue",
border="orange",space=0.1,
density = 15, # con density se consigue el rallado
main = "Gráfico de barras de factor_var2",
xlab = "Niveles de factor_var2",
ylab = "Porcentajes",
cex.names = 0.8,
xaxt = "n")
text(bp01, 0, labels = names(tbfactor_var2ord),
srt = 45, adj = c(1.1,1.1), # pos = 2,
xpd = TRUE)
# Añade texto a las barras
text(x = bp01, y = tbfactor_var2ord, label = paste0(tbfactor_var2ord, " %"),
pos = 1, cex = 0.9, col = "red")14.4.2 Histogramas
# Histograma de la variable num_var1
hist(num_var1, col = "lightblue",
main = "Histograma de num_var1",
xlab = "num_var1",
ylab = "Frecuencia")# Histograma de la variable num_var1 con densidad
hist(num_var1, col = "lightblue",
main = "Histograma de num_var1",
xlab = "num_var1",
ylab = "Densidades",
freq = FALSE)14.4.3 Diagramas de caja
# Diagrama de caja de la variable num_var1
boxplot(num_var1, col = "lightblue",
main = "Diagrama de caja de num_var1")# Diagrama de caja de la variable num_var1 con información adicional
bx1 = boxplot(num_var1, col = "lightblue",
main = "Diagrama de caja de num_var1",
boxwex = 0.5, whisklty = 2, staplelty = 1, outpch = 19, outcol = "red")Información adicional: $stats (estadísticos), $n (número de observaciones), $conf (intervalos), $out (valores atípicos), $group (grupos), $names (nombres de los grupos).
bx1$stats
[,1]
[1,] -1.96661716
[2,] -0.49667731
[3,] 0.06175631
[4,] 0.69499808
[5,] 2.18733299
$n
[1] 100
$conf
[,1]
[1,] -0.1265284
[2,] 0.2500410
$out
[1] -2.309169
$group
[1] 1
$names
[1] ""# Diagrama de caja de la variable num_var1 con color según factor_var1
boxplot(num_var1 ~ factor_var1, col = "lightblue",
main = "Diagrama de caja de num_var1 según factor_var1")# Diagrama de caja horizontal de la variable num_var1
boxplot(num_var1, col = "lightblue", horizontal = TRUE,
main = "Diagrama de caja de num_var1")14.4.4 Gráficos de dispersión y correlación
# Gráfico de dispersión de las variables num_var1 y num_var2
plot(num_var1, num_var2)# Gráfico de dispersión de las variables num_var1 y interaccion1
plot(num_var1, interaccion1)# Gráfico de dispersión de num_var1 y num_var2 con color según factor_var1
plot(num_var1, num_var2, col = factor_var1, pch = 19, cex = 1.5)
14.4.5 La función plot()
Las funciones plot(), points(), lines(), text(), mtext(), axis(), identify() etc nos permitirán dibujar puntos, líneas y texto.
Las siguientes formas de llamar a la función plot() dibujan \(y\) frente a \(x\) (también conocido como nube de puntos o diagrama de dispersión):
x e y tienen que tener el mismo número de elementos.
Probamos con los siguientes ejemplos:
plot(y ~ x,type="l")plot(y ~ x,type="b")plot(y ~ x,type="h")La función points() añade puntos a un gráfico creado con plot(), la función lines() añade líneas, la función text() añade texto en localizaciones específicas, la función mtext() añade texto en uno de los márgenes, y la función axis() da un control más preciso sobre las marcas y etiquetas sobre los ejes.
Con la función spline() nos permite ajustar curvas a los puntos facilitados:
Los parámetros por defecto, tales como el tamaño del texto, el grosor de línea, etc, son generalmente adecuados. La función par() nos permite cambiar los parámetros por defecto.
par(cex=1.25) # cambia el tamaño del textoEl primer uso de par() para hacer cambios al dispositivo actual de dibujo, se almacenan los parámetros existentes, para que puedan ser restaurados más tarde.
par.viejos = par(cex=1.25,mex=1.25) # mex=1.25 expande el margen un 25%En este ejemplo, se han guardado los parámetros existentes en el objeto par.viejos, y además se han cambiado los parámetros: cex y mex. Para restaurar los parámetros a los valores anteriores, introduciríamos la expresión R: par(par.viejos). A continuación, se muestra un ejemplo de uso:
14.4.6 Otros tipos de gráficos
x1 = x2 = seq(0,3,.1) # asignación múltiple permitida!!
funx = function(vx) (vx[1]-2)^4+(vx[1]-2*vx[2])^2
z = outer(x1,x2,FUN=function(x1,x2) ( (x1-2)^4+(x1-2*x2)^2 ) )
# z = matrix(0,nrow=length(x1),ncol=length(x2))
# for (i in 1:length(x1)) {
# for (j in 1:length(x2)) {
# z[i,j] = funx(c(x1[i],x2[j]))
# }
# }
res = persp(x1,x2,z,theta=45,phi=0)
# añadir línea roja
ptos.vx = data.frame(
x = c(0,0,3,3,0,0,3,3),
y = c(0,3,3,0,0,3,3,0)
)
vz = as.matrix(funx(ptos.vx))
lines(trans3d(x=ptos.vx[,1],y=ptos.vx[,2],z=vz,pmat=res),col="red",lwd=2)#ptos.vx = df.res[,3:4]
ptos.vx = data.frame(
x = c(0,0,3,3,0,0,3,3),
y = c(0,3,3,0,0,3,3,0)
)
x <- seq(0, 3.5, length.out=100)
y <- seq(0, 3, length.out=100)
#z <- as.matrix(funx(expand.grid(x, y)))
#contour(x, y, matrix(z, length(x)),xlim=c(0,3.5))
z <- funx(expand.grid(x, y))
contour(x, y, matrix(z$Var1, nrow = length(x)),xlim=c(0,3.5))
lines(ptos.vx,type="o",col="red",pch=3)
grid(col=gray(0.6))
# punto inicial
points(ptos.vx[1,1], ptos.vx[1,2], pch = 20, cex = 2,col="black")
n = nrow(ptos.vx)
# punto final
points(ptos.vx[n,1], ptos.vx[n,2], pch = 20, col = "blue", cex = 3)También puede verse como se mueve en el plano XY (no se usa: contour()):
plot(ptos.vx[,1],ptos.vx[,2],type="l",xlim=c(-0.5,3.5),ylim=c(-0.5,3.5),
xlab="x",ylab="y")
points(ptos.vx[,1],ptos.vx[,2],pch=16)
grid(col=gray(0.6))
# punto inicial
points(ptos.vx[1,1], ptos.vx[1,2], pch = 20, cex = 2,col="red")
n = nrow(ptos.vx)
# punto final
points(ptos.vx[n,1], ptos.vx[n,2], pch = 20, col = "blue", cex = 3)x = 0:3
a=1
f = expression(sin(x)*exp(-a*x))
ffun = function(x,a) eval(f)
(D1fun = deriv(f,"x", hessian = TRUE, func=TRUE))function (x)
{
.expr1 <- sin(x)
.expr4 <- exp(-a * x)
.expr5 <- .expr1 * .expr4
.expr6 <- cos(x)
.expr8 <- .expr4 * a
.expr11 <- .expr6 * .expr8
.value <- .expr5
.grad <- array(0, c(length(.value), 1L), list(NULL, c("x")))
.hessian <- array(0, c(length(.value), 1L, 1L), list(NULL,
c("x"), c("x")))
.grad[, "x"] <- .expr6 * .expr4 - .expr1 * .expr8
.hessian[, "x", "x"] <- -(.expr11 + .expr5 + (.expr11 - .expr1 *
(.expr8 * a)))
attr(.value, "gradient") <- .grad
attr(.value, "hessian") <- .hessian
.value
}14.4.7 Otras cuestiones sobre gráficos
par(mfrow = c(2, 2))
# Gráfico de barras de la variable cualitativa factor_var2
barplot(table(factor_var2), col = "lightblue",
border="orange",space=0.1,
main = "Gráfico de barras de factor_var2",
xlab = "Niveles de factor_var2",
cex.names = 0.8)
# Histograma de la variable num_var1
hist(num_var1, col = "lightblue",
main = "Histograma de num_var1",
xlab = "num_var1",
ylab = "Frecuencia")
# Diagrama de caja de la variable num_var1
boxplot(num_var1, col = "lightblue",
main = "Diagrama de caja de num_var1")
# Gráfico de dispersión de las variables num_var1 y num_var2
plot(num_var1, num_var2)En el siguiente ejemplo, se muestran dos gráficos, donde el de la derecha es una mejora del gráfico de la izquierda. A ambos se les ha añadido texto.
p.viejos = par(mfrow=c(1,2))
library(MASS)
primates = Animals[row.names(Animals) %in% c("Potar monkey",
"Gorilla","Human","Rhesus monkey","Chimp"),]
plot(primates$body,primates$brain)
#' pos=4 # texto a la derecha del punto
text(x=primates$body,y=primates$brain,labels=row.names(primates),pos=4)
##' Gráfico 2
plot(primates$body,primates$brain,pch=16,
xlab="Peso Cuerpo (kg)",ylab="Peso Cabeza (g)",
xlim=c(0,280),ylim=c(0,1350))
text(x=primates$body,y=primates$brain,labels=row.names(primates),pos=4)par(p.viejos)Nota: valores de pos: 1 (inferior), 2 (izquierda), 3 (arriba) y 4 (derecha).
Se ilustra en el siguiente ejemplo el uso de las funciones mtext() y axis().
plot(primates$body,primates$brain,pch=16,
xlab="Peso Cuerpo (kg)",ylab="Peso Cabeza (g)",
xlim=c(0,280),ylim=c(0,1350),
main="Título gráfico",axes=FALSE)
text(x=primates$body,y=primates$brain,labels=row.names(primates),pos=4)
mtext(text = "Subtítulo Y",side=2,line=2)
mtext(text = "Subtítulo X",side=1,line=2)
mtext(text = "Subtítulo",side=3,line=0)
mtext(text = "Comentario 1",side=4,line=0,cex = 0.8,adj=0.05,col="red")
mtext(text = "Comentario 2",side=4,line=0,cex = 0.8,adj=0.95,col="blue")
axis(side=1,tick = T,at=seq(0,300,by=25),labels = seq(0,300,by=25),
col="red",cex.axis=0.9,padj=-0.5,las=0 ) # las=2 etiq. perp.
axis(side=2,tick = T,at=seq(0,1350,by=100),labels = seq(0,1350,by=100),
col="red",cex.axis=0.7,hadj = 0.7,lwd = 2,las=2) #las=2 etiq.perp.
box(lwd=0.5)En el siguiente ejemplo, usaremos el parámetro cex (tamaño carácter), col (color de los símbolos) y pch (símbolo). Nota: type="n" no pinta ningún símbolo.
plot(1,1,xlim=c(1,7.5),ylim=c(1.75,5),type="n",axes=F,xlab="",ylab="")
box()
#' primera fila
points(1:7,rep(4.5,7),cex=1:7,col=1:7,pch=0:6)
#' segunda fila
text(1:7,rep(3.5,7), labels=paste(0:6),cex=1:7,col=1:7)
#' tercera fila
points(1:7,rep(2.5,7), pch=(0:6)+7)
text(1:7,rep(2.5,7), paste((0:6)+7),pos=4)
#' cuarta fila
points(1:7,rep(2,7), pch=(0:6)+14)
text(1:7,rep(2,7), paste((0:6)+14),pos=4)Se pueden utilizar otras paletas de colores con el parámetro col, por ejemplo: col=rainbow(6).
14.4.8 Cómo grabar los gráficos en ficheros gráficos (jpg, png, pdf, …)
- A continuación se crea el fichero “grafico.jpg” en formato “jpg”.
- A continuación se crea el fichero “grafico.png” en formato “png”.
- A continuación se crea el fichero “grafico.pdf” en formato “pdf”.
14.5 Gráficos con el sistema “ggplot2”
14.5.1 Diagramas de barras
library(ggplot2)
datos_CCAA = data.frame(
CCAA = c("Andalucía","Aragón","Asturias","Baleares","Canarias",
"Cantabria","Castilla y León","Castilla-La Mancha",
"Cataluña","Extremadura","Galicia","Madrid","Murcia",
"Navarra","País Vasco","La Rioja","Valencia","Ceuta",
"Melilla"),
TOTALCCAA = c(7.357,1.277,1.076,0.846,1.718,0.527,2.540,1.839,
6.343,1.087,2.772,5.423,1.218,0.527,2.098,0.316,
4.518,0.073,0.068)
)
ggplot(datos_CCAA,aes(x=CCAA,y=TOTALCCAA)) +
geom_col(fill="blue") +
labs(title="Población Española",
subtitle="por Comunidades Autónomas",
y="Población (millones)",x="Comunidades Autónomas",
caption="Fuente: Elaboración propia") +
scale_y_continuous(labels = scales::comma) +
theme(axis.text.x = element_text(angle = 90, hjust = 1)) ggplot(datos_CCAA,aes(x=CCAA,y=TOTALCCAA)) +
geom_col(fill="blue") +
labs(title="Población Española en 2001",
subtitle = "por Comunidades Autónomas",
y="Población (millones)",x="Comunidades Autónomas",
caption="Fuente: Elaboración propia") +
scale_y_continuous(labels = scales::comma) +
theme(axis.text.y = element_text(angle = 0, hjust = 1)) +
coord_flip()Para presentar las columnas siguiendo algún tipo de orden (por defecto, las ordena según el orden alfabético) se puede utilizar la función reorder(). Cuando se llama a reorder() el primer argumento indica la columna que se usará para las etiquetas, y la segunda columna será para indicar el orden en el que aparecerán (si se quiere presentar en orden contrario se debe colocar un signo “-” delante del segundo argumento).
p0 = ggplot(datos_CCAA,aes(x=reorder(CCAA,TOTALCCAA),y=TOTALCCAA)) +
geom_col(fill="blue") +
labs(title="Población Española",
subtitle = "por Comunidades Autónomas",
y="Población (millones)",x="Comunidades Autónomas",
caption="Fuente: Elaboración propia") +
scale_y_continuous(labels = scales::comma) +
theme(axis.text.y = element_text(angle = 0, hjust = 1)) +
coord_flip()
p014.5.2 Diagramas de líneas
datos3 = data.frame(
Año = c(2011,2012,2013,2014,2015,2016),
TBN = c(10.630451,10.221912,9.652501,9.782435,9.600260,9.449450)
)library(ggplot2) # ya cargado con library(tidyverse)
library(ggthemes)
p1 = ggplot(datos3, aes(x = Año, y=TBN)) +
geom_line(alpha = 1,linetype = "solid", colour="blue",linewidth = 1) +
geom_point(size = 2) +
labs(title="Tasa bruta de Natalidad (x 1.000) ",
subtitle = "Andalucía. 2010-2016",
y="Tasa bruta de natalidad",
x="Años",
caption="Fuente: Elaboración propia") +
#scale_y_continuous(labels = scales::comma,breaks = seq(0,3.5,by=0.25)) +
scale_x_continuous(breaks = seq(2010,2016,by=1)) +
theme(axis.text.y = element_text(angle = 0, hjust = 1)) +
theme_solarized()
p1# datos simulados
set.seed(123)
datos4 = data.frame(
Edades = rep(0:100,2),
dx = floor(runif(202, min=0, max=100)),
Sexo = rep(c("Hombres","Mujeres"),each=101)
)
rbind(datos4[1:4,], datos4[199:202,]) Edades dx Sexo
1 0 28 Hombres
2 1 78 Hombres
3 2 40 Hombres
4 3 88 Hombres
199 97 15 Mujeres
200 98 57 Mujeres
201 99 23 Mujeres
202 100 96 Mujeresp2 = ggplot(datos4, aes(x = Edades, y=dx, group = Sexo, colour = Sexo)) +
geom_line(alpha = 1,
linetype = "solid",
linewidth = 0.5) +
labs(title="Defunciones teóricas por sexo. Tablas Vida",
subtitle = "Andalucía. 2015.",
y="Defunciones teóricas (dx)",
x="Edades",
caption="Fuente: Elaboración propia") +
#scale_y_continuous(labels = scales::comma,breaks = seq(0,1,by=0.1)) +
#scale_x_continuous(breaks = c(0,seq(5,100,by=5))) +
scale_x_discrete(breaks = c(0,seq(5,100,by=5))) +
theme(axis.text.y = element_text(angle = 0, hjust = 1)) +
theme_solarized()
p214.5.3 Integración Monte Carlo
circle <- function(x)
{
return(sqrt(1-x^2))
}
ggplot(data.frame(x = c(0, 1)), aes(x)) +
geom_function(fun = circle)ggplot(data.frame(x = seq(0, 1, 1e-4)), aes(x)) +
geom_area(aes(x = x,
y = ifelse(x^2 + circle(x)^2 <= 1, circle(x), 0)),
fill = "pink") +
geom_function(fun = circle)B <- 1e4
unif_points <- data.frame(x = runif(B), y = runif(B))ggplot(unif_points, aes(x, y)) +
geom_area(aes(x = x,
y = ifelse(x^2 + circle(x)^2 <= 1, circle(x), 0)),
fill = "pink") +
geom_point(size = 0.5, alpha = 0.25,
colour = ifelse(unif_points$x^2 + unif_points$y^2 <= 1,
"red", "black")) +
geom_function(fun = circle)mean(unif_points$x^2 + unif_points$y^2 <= 1)[1] 0.7949En este caso, se puede calcular el área de forma exacta: \(\int_0^1 \sqrt{1-x^2}\ dx = \frac{\pi}{4} = 0.7853...\). Sin embargo, para integrales más complicadas, pueden ser necesarios métodos de integración numérica como la integración de Monte Carlo.
14.5.4 Gráficos de Estadística Descriptiva Básica
datos2 = data.frame(X = c(3,2,4,2,1,2,5,2,3,2),
Y = c(2,5,4,3,3,4,4,3,2,3))tabfrec = datos2 %>%
group_by(X) %>%
summarise(
n = n(),
percent = n()/nrow(.)) %>%
rename(ni = n,fi=percent) %>%
mutate(pi = fi*100,
Ni = cumsum(ni),
Fi = cumsum(fi),
Pi = Fi*100)
tabfrec# A tibble: 5 × 7
X ni fi pi Ni Fi Pi
<dbl> <int> <dbl> <dbl> <int> <dbl> <dbl>
1 1 1 0.1 10 1 0.1 10
2 2 5 0.5 50 6 0.6 60
3 3 2 0.2 20 8 0.8 80
4 4 1 0.1 10 9 0.9 90
5 5 1 0.1 10 10 1 100# tabfrec es una tabla de frecuencias
ggplot(tabfrec,aes(x="", y=pi, fill=factor(X))) +
geom_bar(width = 1, stat = "identity") +
coord_polar("y", start=0) +
theme_void() +
geom_text(aes(label=paste0(X," - ",round(pi,2), "%")),
position = position_stack(vjust = 0.5),
size = 4)# tabfrec es una tabla de frecuencias
ggplot(tabfrec,aes(x=X, y=Fi)) +
geom_step() +
coord_cartesian(ylim = c(0,1)) # xlimX2 = c(0.2,0.6,1.1,1.7,1.9,3.7,3.8,4.2,4.5,4.8,5.3,5.7,
6.2,6.7,7.5,8.1,8.5,8.7,9.2,9.5)
extremos = c(0,1,3,5,6,8,10)
m = length(extremos)
marcas = (extremos[1:(m-1)]+extremos[2:m])/2
X2int=cut(X2,breaks=extremos) #agrupamos en intervalos
ai = diff(extremos)
datosInt = data.frame(X=X2int)
tabfrecInt = datosInt %>%
group_by(X) %>%
summarise(
n = n(),
percent = n()/nrow(.)) %>%
rename(ni = n,fi=percent) %>%
mutate(xi = marcas,
fi = round(ni/sum(ni),4),
pi = fi*100,
Ni = cumsum(ni),
Fi = cumsum(fi),
Pi = Fi*100,
ai = ai,
hini = ni/ai,
hifi = fi/ai)
tabfrecInt# A tibble: 6 × 11
X ni fi xi pi Ni Fi Pi ai hini hifi
<fct> <int> <dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl> <dbl> <dbl>
1 (0,1] 2 0.1 0.5 10 2 0.1 10 1 2 0.1
2 (1,3] 3 0.15 2 15 5 0.25 25 2 1.5 0.075
3 (3,5] 5 0.25 4 25 10 0.5 50 2 2.5 0.125
4 (5,6] 2 0.1 5.5 10 12 0.6 60 1 2 0.1
5 (6,8] 3 0.15 7 15 15 0.75 75 2 1.5 0.075
6 (8,10] 5 0.25 9 25 20 1 100 2 2.5 0.125Intercambiar los ejes:
p +
coord_flip()p3 = ggplot(datos.salarios,
aes(y=salario,color=factor(seguro.medico))) +
geom_boxplot(outlier.shape = 1) +
coord_flip() +
theme(axis.text.y=element_blank(),
axis.ticks.y = element_blank())
p3datos2C = data.frame(X=c(3,2,4,2,1,2,5,2,3,2),
Y=c(2,5,4,3,3,4,4,3,2,3))
ggplot(datos2C) +
geom_point(aes(x=X, y=Y), color="blue") 14.5.5 Gráficos comparativos
14.5.5.1 Diagramas de barras
[1] "X" "estado.salud" "hizo.ejercicio" "cobertura.medica" "fumado.100cig" "altura.cm"
[7] "peso.kilos" "peso.deseado" "edad" "sexo" library(janitor)
datos10 %>%
tabyl(estado.salud,hizo.ejercicio) %>%
adorn_totals("row") %>%
adorn_totals("col") %>%
adorn_percentages("all") %>%
adorn_pct_formatting(digits = 2) %>%
adorn_ns() %>%
adorn_title() hizo.ejercicio
estado.salud No Si Total
Mala 1.40% (14) 1.40% (14) 2.80% (28)
Regular 5.20% (52) 5.30% (53) 10.50% (105)
Buena 8.40% (84) 19.80% (198) 28.20% (282)
Muy buena 6.60% (66) 27.80% (278) 34.40% (344)
Excelente 3.30% (33) 20.80% (208) 24.10% (241)
Total 24.90% (249) 75.10% (751) 100.00% (1,000)Intercambiando las variables:
Con la ordenación por defecto:
Ordenando de forma manual:
Ordenando según el valor de alguna variable:
Nota: las distribuciones condicionadas son muy indicadas cuando se quieren comparar características en grupos de individuos con tamaño diferente.
Proporciones con dodge
Con proporciones condicionadas (uso en aes() de group):
Con porcentajes:
datos10 %>%
ggplot(aes(x=estado.salud,group=hizo.ejercicio)) +
geom_bar(aes(y=..prop..,fill=hizo.ejercicio),
position= "dodge") +
geom_text(aes(label = scales::percent(..prop..), y= ..prop.. ),
stat= "count", vjust = -.5,
position = position_dodge(width = 1)) +
labs(y="Porcentajes") +
scale_y_continuous(labels = scales::percent)NOTA: en este gráfico se puede observar que las dos variables no son independientes, para ello, sobre cada uno de los valores de “estado.salud” (en el eje X) las barras rojas (no hizo ejercicio) y verdes (sí hizo ejercicio) deberían tener la misma altura.
Las tablas de frecuencias condicionadas son:
datos10 %>%
tabyl(estado.salud,hizo.ejercicio) %>%
adorn_totals("row") %>%
adorn_totals("col") %>%
adorn_percentages("col") %>%
adorn_pct_formatting(digits = 1) %>%
adorn_ns() %>%
adorn_title() hizo.ejercicio
estado.salud No Si Total
Mala 5.6% (14) 1.9% (14) 2.8% (28)
Regular 20.9% (52) 7.1% (53) 10.5% (105)
Buena 33.7% (84) 26.4% (198) 28.2% (282)
Muy buena 26.5% (66) 37.0% (278) 34.4% (344)
Excelente 13.3% (33) 27.7% (208) 24.1% (241)
Total 100.0% (249) 100.0% (751) 100.0% (1,000)Con proporciones condicionadas (uso en aes() de group):
Se pueden colocar etiquetas sobre las barras con los porcentajes:
ggplot(datos10,aes(x=estado.salud,fill=hizo.ejercicio)) +
geom_bar(position="fill") +
coord_flip()Intercambiando las variables:
ggplot(datos10,aes(x=hizo.ejercicio,fill=estado.salud)) +
geom_bar(position="fill") +
coord_flip()14.5.5.2 Con Diagramas de cajas y bigotes
Pasamos de formato ancho a formato largo de los datos:
F = c(3,4,6,7,5,8,7,3,5,4,8,5,5,8,8,8,5)
L = c(5, 5, 8, 7, 7, 9, 10, 4, 7, 4, 10, 5, 7, 9, 10, 5, 7)
n = length(F)
t115largo = tibble(
Calificacion = c(F,L),
Asignatura = c(rep("F",n),rep("L",n))
)
head(t115largo)# A tibble: 6 × 2
Calificacion Asignatura
<dbl> <chr>
1 3 F
2 4 F
3 6 F
4 7 F
5 5 F
6 8 F t115largo %>%
ggplot(aes(x=Asignatura,y=Calificacion,fill=Asignatura)) +
geom_boxplot() +
coord_flip()t115largo %>%
ggplot(aes(x=Asignatura,y=Calificacion,fill=Asignatura)) +
geom_boxplot(outlier.colour = "red", outlier.shape = 1) +
geom_point() +
scale_fill_brewer(palette="Blues") +
stat_summary(fun=mean, geom="point", color = "blue",shape=23, size=4) +
scale_x_discrete(limits=c("L", "F")) +
coord_flip()Puede hacerse al agrupar sobre una de las variables con ayuda de las funciones de ggplot2:
-
cut.width: considera intervalos de anchura fijada. -
cut.interval: considera intervalos de igual ancho fijo. -
cut.number: considera intervalos para que contengan un número de observaciones fijo (aproximadamente).
ggplot(diamonds, aes(x=carat, y=price)) +
geom_boxplot(aes(group = cut_width(carat, 0.25)),
outlier.colour = "red")Ajustar la transparencia de los outliers usando el argumento outlier.alpha:
ggplot(diamonds, aes(x=carat, y=price)) +
geom_boxplot(aes(group = cut_width(carat, 0.25)),
outlier.colour = "red",
outlier.alpha = 0.1)# use stat = "identity":
y <- rnorm(100)
df <- data.frame(
x = 1,
y0 = min(y),
y25 = quantile(y, 0.25),
y50 = median(y),
y75 = quantile(y, 0.75),
y100 = max(y)
)
df2 = data.frame(Y = y)
p1a = ggplot(df, aes(x)) +
geom_boxplot(
aes(ymin = y0, lower = y25, middle = y50, upper = y75, ymax = y100),
stat = "identity"
) + coord_flip()
p1b = ggplot(df2, aes(x = Y)) +
geom_boxplot(col = "red", fill = "blue", alpha = 0.5)
par(mfrow = c(1,2))
p1a p1b14.6 Gráficos dinámicos
14.6.1 Gráficos interactivos con plotly
14.6.2 Gráficos interactivos con dygraphs
14.6.3 Gráficos interactivos con highcharter
Código
library(highcharter)
library(dplyr)
library(lubridate)
library(purrr)
# Crear datos de ejemplo
set.seed(123)
timestamps <- seq(
from = as.POSIXct("2024-01-28 00:00:00"),
to = as.POSIXct("2024-01-28 23:50:00"),
by = "10 mins"
)
datos <- data.frame(
timestamp = timestamps,
bateria = c(
seq(80, 60, length.out = 36),
seq(60, 90, length.out = 36),
seq(90, 75, length.out = 36),
seq(75, 80, length.out = 36)
),
generacion = c(
rep(0, 36),
seq(0, 5, length.out = 36),
seq(5, 0, length.out = 36),
rep(0, 36)
),
precio = c(
rep(0.08, 36),
seq(0.08, 0.25, length.out = 18),
seq(0.25, 0.15, length.out = 18),
seq(0.15, 0.30, length.out = 36),
seq(0.30, 0.08, length.out = 36)
)
)
# Preparar datos para highcharter
datos_hc <- list(
bateria = map2(
as.numeric(datos$timestamp) * 1000, # Convertir a timestamp de JavaScript
datos$bateria,
function(x, y) list(x = x, y = y)
),
generacion = map2(
as.numeric(datos$timestamp) * 1000,
datos$generacion,
function(x, y) list(x = x, y = y)
),
precio = map2(
as.numeric(datos$timestamp) * 1000,
datos$precio,
function(x, y) list(x = x, y = y)
)
)
# Crear el gráfico
hc <- highchart() %>%
hc_chart(type = "area") %>%
# Título
hc_title(
text = "Monitorización Diaria: Batería, Generación y Precio"
) %>%
# Eje X
hc_xAxis(
type = "datetime",
crosshair = TRUE
) %>%
# Ejes Y
hc_yAxis_multiples(
list(
title = list(text = "Batería (%)", style = list(color = "#1E90FF")),
labels = list(format = "{value}%", style = list(color = "#1E90FF")),
min = 0,
max = 100
),
list(
title = list(text = "Generación (kW)", style = list(color = "#FFA500")),
labels = list(format = "{value} kW", style = list(color = "#FFA500")),
opposite = TRUE,
min = 0,
max = 6
),
list(
title = list(text = "Precio (€/kWh)", style = list(color = "#32CD32")),
labels = list(format = "{value}€", style = list(color = "#32CD32")),
opposite = TRUE,
min = 0,
max = 0.35
)
) %>%
# Series
hc_add_series(
data = datos_hc$bateria,
name = "Batería",
color = "#1E90FF",
fillOpacity = 0.3,
yAxis = 0
) %>%
hc_add_series(
data = datos_hc$generacion,
name = "Generación",
color = "#FFA500",
fillOpacity = 0.3,
yAxis = 1
) %>%
hc_add_series(
data = datos_hc$precio,
name = "Precio",
color = "#32CD32",
fillOpacity = 0.3,
yAxis = 2
) %>%
# Tooltips
hc_tooltip(
shared = TRUE,
crosshairs = TRUE,
headerFormat = "<b>{point.x:%H:%M}</b><br/>",
pointFormat = "<span style='color:{series.color}'>{series.name}</span>: <b>{point.y:.2f}</b><br/>"
) %>%
# Leyenda
hc_legend(
align = "center",
verticalAlign = "bottom",
layout = "horizontal"
) %>%
# Opciones de área
hc_plotOptions(
area = list(
stacking = NULL,
lineWidth = 1,
marker = list(
enabled = FALSE,
symbol = "circle",
radius = 2,
states = list(
hover = list(enabled = TRUE)
)
),
states = list(
hover = list(lineWidth = 2)
)
)
) %>%
# Exportación
hc_exporting(enabled = TRUE) %>%
# Zoom
hc_chart(zoomType = "x")
# Mostrar el gráfico
hc15 Probabilidad
Se recomienda visitar las aplicaciones web didácticas-interactivas para manipular distribuciones de probabilidad:
15.1 Distribuciones de probabilidad
| Distribución | Función de densidad | Función de distribución | Función cuantil | Función de probabilidad |
|---|---|---|---|---|
| Normal | dnorm() |
pnorm() |
qnorm() |
rnorm() |
| T-Student | dt() |
pt() |
qt() |
rt() |
| F-Snedecor | df() |
pf() |
qf() |
rf() |
| Chi-cuadrado | dchisq() |
pchisq() |
qchisq() |
rchisq() |
| Binomial | dbinom() |
pbinom() |
qbinom() |
rbinom() |
| Poisson | dpois() |
ppois() |
qpois() |
rpois() |
| Hipergeométrica | dhyper() |
phyper() |
qhyper() |
rhyper() |
# Función de densidad de la distribución normal
dnorm(0, mean = 0, sd = 1)[1] 0.3989423# Función de probabilidad de una binomial con 10 ensayos y probabilidad 0.5
dbinom(5, size = 10, prob = 0.5)[1] 0.2460938# Función de probabilidad de una Poisson con lambda 2
dpois(5, lambda = 2)[1] 0.03608941# Función de probabilidad de una Hipergeométrica con 10 bolas, 5 blancas y 5 negras
dhyper(2, m = 5, n = 5, k = 10)[1] 0# Función de probabilidad de una Binomial negativa con 5 éxitos y probabilidad 0.5
dnbinom(2, size = 5, prob = 0.5)[1] 0.1171875# Función de distribución de la distribución normal
pnorm(1.96, mean = 0, sd = 1)[1] 0.9750021# Función de distribución de una Binomial con 5 ensayos y probabilidad 0.5
pbinom(2, size = 5, prob = 0.5)[1] 0.5# Función de distribución de una Poisson con lambda 2
ppois(5, lambda = 2)[1] 0.9834364# Función de distribución de una Exponencial con lambda 2
pexp(2, rate = 2)[1] 0.9816844# Función cuantil de la distribución normal
qnorm(0.975, mean = 0, sd = 1)[1] 1.959964# Función cuantil de la distribución t-Student
qt(0.975, df = 10)[1] 2.228139# Función cuantil de la distribución F-Snedecor
qf(0.975, df1 = 5, df2 = 10)[1] 4.236086# Función cuantil de la distribución Chi-cuadrado
qchisq(0.975, df = 5)[1] 12.8325# Genera valores de una distribución normal
rnorm(10, mean = 0, sd = 1) [1] -0.56047565 -0.23017749 1.55870831 0.07050839 0.12928774 1.71506499 0.46091621 -1.26506123 -0.68685285
[10] -0.44566197# Genera valores de una distribución t-Student
rt(10, df = 10) [1] 1.18942191 0.41170946 -0.41226883 0.97822144 -0.99963708 -0.30305368 -0.07190032 -0.21130955 -0.92603370
[10] 0.48313427# Genera valores de una distribución F-Snedecor
rf(10, df1 = 5, df2 = 10) [1] 0.5680880 1.0753056 0.7462000 0.3176353 0.4779375 0.2694212 0.4360031 0.6511190 1.8898213 0.3253912También se han visto más funciones R en el apartado Sección 5.7.
16 Tratamiento de datos: Análisis inferencial
16.1 Contrastes de hipótesis
Se recomienda visitar la aplicación web:
Contrastes de Hipótesis de Inferencia Paramétrica (en inglés): aplicación web para realizar contrastes de hipótesis de inferencia paramétrica.
-
DIAGRAMA DE FLUJOS EN PDF que ayudará a elegir qué test se tendría que utilizar según un árbol de decisión: “What statistical test should I do? (pdf)”.
- Nota: al hacer click sobre los tests-contrastes nos dirige a una página del autor en el qué explica dicho test.
16.1.1 Contrastes de Normalidad (No paramétricos)
# Contraste de normalidad de Shapiro-Wilk
shapiro.test(num_var1)
Shapiro-Wilk normality test
data: num_var1
W = 0.99388, p-value = 0.9349# Contraste de normalidad de Lilliefors
lillie.test(num_var1)
Lilliefors (Kolmogorov-Smirnov) normality test
data: num_var1
D = 0.058097, p-value = 0.557516.1.2 Contrastes paramétricos de medias y varianzas
Para usar los contrastes paramétricos, en primer lugar, se deben aceptar las hipótesis de normalidad adecuadas, realizando contrastes de Normalidad (más utilizado es el test de Shapiro-Wilk).
-
Se recomienda visitar las siguientes aplicaciones web de tipo didáctico que permiten trabajar con la distribución muestrales de la media muestral:
Con variables continuas: “Sampling Distribution of the Sample Mean”
Con variables discretas: “Sampling Distribution of the Sample Mean”
Inferencia sobre la media poblacional “Inference for a Population Mean”
Interpretación de los intervalos de confianza (explicado sobre proporción y media) “Interpretation of Confidence Intervals”
Errores y Potencia en contrastes de hipótesis (proporción y media poblacional): “Errors and Power in Significance Testing”
Bootstrap para una muestra: “The Bootstrap For One Sample”
- Bilateral
# Contraste de medias de una variable numérica
t.test(num_var1, mu = 0) # alternative = ""two.sided"
One Sample t-test
data: num_var1
t = 0.99041, df = 99, p-value = 0.3244
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
-0.09071657 0.27152838
sample estimates:
mean of x
0.09040591 # Contraste de medias de una variable numérica
t.test(num_var1, mu = 1) # alternative = ""two.sided"
One Sample t-test
data: num_var1
t = -9.9647, df = 99, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 1
95 percent confidence interval:
-0.09071657 0.27152838
sample estimates:
mean of x
0.09040591 - Unilateral
# Contraste de medias de una variable numérica
t.test(num_var1, mu = 0, alternative = "greater")
One Sample t-test
data: num_var1
t = 0.99041, df = 99, p-value = 0.1622
alternative hypothesis: true mean is greater than 0
95 percent confidence interval:
-0.06115723 Inf
sample estimates:
mean of x
0.09040591 # Contraste de medias de una variable numérica
t.test(num_var1, mu = 0, alternative = "less")
One Sample t-test
data: num_var1
t = 0.99041, df = 99, p-value = 0.8378
alternative hypothesis: true mean is less than 0
95 percent confidence interval:
-Inf 0.2419691
sample estimates:
mean of x
0.09040591 Ver la definición de la función var_test_1var() en el apartado Sección 12.4.2.
# Contraste de varianza de una variable numérica
# Ejemplo de uso
set.seed(123)
datos <- rnorm(30, mean = 0, sd = 2)
resultado_detallado <- var_test_1var(datos, var0 = 4)
resultado_detallado$estadistico
[1] 27.91022
$p_valor
[1] 0.954565
$varianza_muestra
[1] 3.849685
$varianza_hipotesis
[1] 4
$ic_lower
[1] 2.441717
$ic_upper
[1] 6.957086
$decision
[1] "No rechazar H0"16.1.3 Contraste dos variables independientes
- Bilateral
# Contraste de varianzas de dos variables numéricas
var.test(num_var1, num_var2)
F test to compare two variances
data: num_var1 and num_var2
F = 0.0038473, num df = 99, denom df = 99, p-value < 2.2e-16
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.002588592 0.005717917
sample estimates:
ratio of variances
0.003847253 - Unilateral
# Contraste de varianzas de dos variables numéricas
var.test(num_var1, num_var2, alternative = "greater")
F test to compare two variances
data: num_var1 and num_var2
F = 0.0038473, num df = 99, denom df = 99, p-value = 1
alternative hypothesis: true ratio of variances is greater than 1
95 percent confidence interval:
0.002759744 Inf
sample estimates:
ratio of variances
0.003847253 # Contraste de varianzas de dos variables numéricas
var.test(num_var1, num_var2, alternative = "less")
F test to compare two variances
data: num_var1 and num_var2
F = 0.0038473, num df = 99, denom df = 99, p-value < 2.2e-16
alternative hypothesis: true ratio of variances is less than 1
95 percent confidence interval:
0.000000000 0.005363306
sample estimates:
ratio of variances
0.003847253 Se recomienda visitar las siguientes aplicaciones web que permiten realizar los contrastes:
Comparar dos medias: “Compare Two Means”
Comparar dos muestras con Bootstrap: “Bootstrap for Two Samples”
- Bilaterales
# Contraste de medias de dos variables numéricas
t.test(num_var1, num_var2, var.equal = TRUE)
Two Sample t-test
data: num_var1 and num_var2
t = -50.331, df = 198, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-77.11990 -71.30446
sample estimates:
mean of x mean of y
0.09040591 74.30258451 # Contraste de medias de una variable numérica frente a un factor
t.test(num_var1 ~ factor_var1, var.equal = TRUE)
Two Sample t-test
data: num_var1 by factor_var1
t = -1.3774, df = 98, p-value = 0.1715
alternative hypothesis: true difference in means between group Categoría 1 and group Categoría 2 is not equal to 0
95 percent confidence interval:
-0.6109942 0.1103257
sample estimates:
mean in group Categoría 1 mean in group Categoría 2
-0.0347612 0.2155730 - Unilaterales
# Contraste de medias de dos variables numéricas
t.test(num_var1, num_var2, alternative = "greater", var.equal = TRUE)
Two Sample t-test
data: num_var1 and num_var2
t = -50.331, df = 198, p-value = 1
alternative hypothesis: true difference in means is greater than 0
95 percent confidence interval:
-76.6489 Inf
sample estimates:
mean of x mean of y
0.09040591 74.30258451 # Contraste de medias de dos variables numéricas
t.test(num_var1, num_var2, alternative = "less", var.equal = TRUE)
Two Sample t-test
data: num_var1 and num_var2
t = -50.331, df = 198, p-value < 2.2e-16
alternative hypothesis: true difference in means is less than 0
95 percent confidence interval:
-Inf -71.77546
sample estimates:
mean of x mean of y
0.09040591 74.30258451 - Bilaterales
# Contraste de medias de dos variables numéricas
t.test(num_var1, num_var2, var.equal = FALSE)
Welch Two Sample t-test
data: num_var1 and num_var2
t = -50.331, df = 99.762, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-77.13761 -71.28675
sample estimates:
mean of x mean of y
0.09040591 74.30258451 # Contraste de medias de una variable numérica frente a un factor
t.test(num_var1 ~ factor_var1, var.equal = FALSE)
Welch Two Sample t-test
data: num_var1 by factor_var1
t = -1.3774, df = 97.999, p-value = 0.1715
alternative hypothesis: true difference in means between group Categoría 1 and group Categoría 2 is not equal to 0
95 percent confidence interval:
-0.6109942 0.1103258
sample estimates:
mean in group Categoría 1 mean in group Categoría 2
-0.0347612 0.2155730 - Unilaterales
# Contraste de medias de dos variables numéricas
t.test(num_var1, num_var2, alternative = "greater", var.equal = FALSE)
Welch Two Sample t-test
data: num_var1 and num_var2
t = -50.331, df = 99.762, p-value = 1
alternative hypothesis: true difference in means is greater than 0
95 percent confidence interval:
-76.66023 Inf
sample estimates:
mean of x mean of y
0.09040591 74.30258451 16.1.4 Contraste dos variables dependientes
Nota: Para realizar un contraste de medias de dos variables dependientes, se debe realizar un contraste de Normalidad sobre la diferencia de las variables. Por ejemplo, estudiar: shapiro.test(num_var1 - num_var2).
# Contraste de medias de dos variables numéricas dependientes
t.test(num_var1, num_var2, paired = TRUE)
Paired t-test
data: num_var1 and num_var2
t = -50.505, df = 99, p-value < 2.2e-16
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
-77.12781 -71.29655
sample estimates:
mean difference
-74.21218 # Contraste de medias de dos variables a partir de la diferencia
# Es un contraste unidimiensional
t.test(num_var1 - num_var2)
One Sample t-test
data: num_var1 - num_var2
t = -50.505, df = 99, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
-77.12781 -71.29655
sample estimates:
mean of x
-74.21218 # Contraste de medias de una variable numéricas según un factor
t.test(num_var1 ~ factor_var1, paired = TRUE)
Paired t-test
data: num_var1 by factor_var1
t = -1.3428, df = 49, p-value = 0.1855
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
-0.6249747 0.1243063
sample estimates:
mean difference
-0.2503342 16.1.5 Contrastes de proporciones
Se recomienda visitar las siguientes aplicaciones web que permiten realizar los contrastes:
Comparar dos proporciones: “Compare Two Proportions”
Sobre el Test Chi-Cuadrado (bondad de ajuste/homogeneidad e independencia): Aplicación didáctica-interactiva para realizar manipulaciones con el Test Chi-Cuadrado: “The Chi-Squared Test”
Asociación entre dos variables categóricas (tablas 2x2) con distribuciones Bootstrap y Permutación: Association Between Two Categorical Variables (2x2 Tables)”
Sobre el Test de Fisher (homogeneidad e independencia en tablas 2x2): “Fisher’s Eact Test”
Distribuciones muestrales: “Sampling Distribution of the Sample Proportion”
caras <- rbinom(1, size = 100, prob = .30)
# con corrección continuidad de Yates TRUE por defecto
prop.test(x = caras, n = 100)
1-sample proportions test with continuity correction
data: caras out of 100, null probability 0.5
X-squared = 10.89, df = 1, p-value = 0.0009668
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
0.2411558 0.4320901
sample estimates:
p
0.33 prop.test(x = caras, n = 100, correct = FALSE) # sin Yates
1-sample proportions test without continuity correction
data: caras out of 100, null probability 0.5
X-squared = 11.56, df = 1, p-value = 0.0006739
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
0.2456312 0.4269466
sample estimates:
p
0.33 caras <- rbinom(1, size = 100, prob = .30)
# con probabilidad de la hipótesis nula igual a 0.25
prop.test(x = caras, n = 100, p = 0.25)
1-sample proportions test with continuity correction
data: caras out of 100, null probability 0.25
X-squared = 0.013333, df = 1, p-value = 0.9081
alternative hypothesis: true p is not equal to 0.25
95 percent confidence interval:
0.1626655 0.3376911
sample estimates:
p
0.24 prop.test(x = caras, n = 100, p = 0.25, correct = FALSE) # sin Yates
1-sample proportions test without continuity correction
data: caras out of 100, null probability 0.25
X-squared = 0.053333, df = 1, p-value = 0.8174
alternative hypothesis: true p is not equal to 0.25
95 percent confidence interval:
0.1669133 0.3323234
sample estimates:
p
0.24 # Contraste de proporciones de una variable categórica
table(factor_var1) # Categoría 1 es éxito y Categoría 2 es fracasofactor_var1
Categoría 1 Categoría 2
50 50
1-sample proportions test without continuity correction
data: table(factor_var1), null probability 0.5
X-squared = 0, df = 1, p-value = 1
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
0.4038315 0.5961685
sample estimates:
p
0.5
1-sample proportions test with continuity correction
data: table(factor_var1), null probability c(0.3)
X-squared = 18.107, df = 1, p-value = 2.088e-05
alternative hypothesis: true p is not equal to 0.3
95 percent confidence interval:
0.3990211 0.6009789
sample estimates:
p
0.5 # Contraste de proporciones de dos variables categóricas
prop.test(x = c(32,20,48), n = c(100,100,100), p = c(0.3, 0.2, 0.5))
3-sample test for given proportions without continuity correction
data: c(32, 20, 48) out of c(100, 100, 100), null probabilities c(0.3, 0.2, 0.5)
X-squared = 0.35048, df = 3, p-value = 0.9503
alternative hypothesis: two.sided
null values:
prop 1 prop 2 prop 3
0.3 0.2 0.5
sample estimates:
prop 1 prop 2 prop 3
0.32 0.20 0.48 table(factor_var2, factor_var1) factor_var1
factor_var2 Categoría 1 Categoría 2
Grupo A 16 14
Grupo B 20 15
Grupo C 14 21# Contraste de proporciones de dos variables categóricas
# Contraste de igualdad de proporciones para 3 grupos
prop.test(x = table(factor_var2, factor_var1)) # 2 columnas
3-sample test for equality of proportions without continuity correction
data: table(factor_var2, factor_var1)
X-squared = 2.2476, df = 2, p-value = 0.325
alternative hypothesis: two.sided
sample estimates:
prop 1 prop 2 prop 3
0.5333333 0.5714286 0.4000000
3-sample test for equality of proportions without continuity correction
data: c(16, 20, 14) out of c(30, 35, 35)
X-squared = 2.2476, df = 2, p-value = 0.325
alternative hypothesis: two.sided
sample estimates:
prop 1 prop 2 prop 3
0.5333333 0.5714286 0.4000000 # Contraste de igualdad de proporciones de fumadores para 4 grupos de pacientes
fumadores <- c( 83, 90, 129, 70 )
pacientes <- c( 86, 93, 136, 82 )
prop.test(x = fumadores, n = pacientes)
4-sample test for equality of proportions without continuity correction
data: fumadores out of pacientes
X-squared = 12.6, df = 3, p-value = 0.005585
alternative hypothesis: two.sided
sample estimates:
prop 1 prop 2 prop 3 prop 4
0.9651163 0.9677419 0.9485294 0.8536585 # Ejemplo con datos pareados
antes <- c(1,1,0,1,0,1,1,0,0,1) # 1: éxito, 0: fracaso
despues <- c(1,1,1,1,0,0,1,1,1,1)
# Crear tabla de contingencia
tabla <- table(antes, despues)
resultado <- mcnemar.test(tabla)
print(resultado)
McNemar's Chi-squared test with continuity correction
data: tabla
McNemar's chi-squared = 0.25, df = 1, p-value = 0.6171-
prop.test()puede usarse para contrastar la hipótesis nula de que las proporciones (probabilidades de éxito) en varios grupos sea la misma, o que sean iguales a ciertos valores dados.
prop.test(x, n, p = NULL,
alternative = c("two.sided", "less", "greater"),
conf.level = 0.95, correct = TRUE)-
“x”: Puede ser:
un vector de conteos de éxitos,
una tabla unidimensional con dos entradas,
o una tabla bidimensional (o matriz) con 2 columnas, que da los conteos de éxitos y fracasos, respectivamente.
“n”: un vector de conteos de ensayos; ignorado si “x” es una matriz o tabla.
“p”: un vector de probabilidades de éxito. Si se especifica, se utiliza como el valor de la probabilidad de éxito en la hipótesis nula. Si no se especifica, se calcula como la suma de los éxitos dividida por la suma de los ensayos.
“alternative”: un caracter que especifica la hipótesis alternativa y debe ser una de “two.sided” (por defecto), “greater” o “less”. Puede especificarse solo con la primera letra. Solo se utiliza para probar la nula que una sola proporción es igual a un valor dado, o que dos proporciones son iguales; de lo contrario, se ignora.
“conf.level”: el nivel de confianza deseado, un número entre 0 y 1. Solo se utiliza para probar la nula que una sola proporción es igual a un valor dado, o que dos proporciones son iguales; de lo contrario, se ignora.
“correct”: un lógico que indica si se debe aplicar la corrección de continuidad de Yates cuando sea posible.
statistic: el valor del estadístico de prueba de chi-cuadrado de Pearson.parameter: los grados de libertad de la distribución chi-cuadrado aproximada del estadístico de prueba.p.value: el p-valor del contraste.estimate: un vector con las proporciones muestrales x/n.conf.int: un intervalo para la proporción verdadera si hay un solo grupo, o para la diferencia en proporciones si hay 2 grupos y p no se da, o NULL de lo contrario. En los casos en que no es NULL, el intervalo de confianza devuelto tiene un nivel de confianza asintótico como se especifica por conf.level, y es apropiado para la hipótesis alternativa especificada.conf.level: el nivel de confianza del intervalo de confianza obtenido. Debe ser un número entre 0 y 1. Solo usado cuando se prueba la hipótesis nula de que una proporción simple es igual a un valor dado, o que dos proporciones son iguales; ignorado en otro caso.correct: un lógico indicando si la corrección de continuidad de Yates se aplicó.
Se realiza un contraste de hipótesis sobre una proporción en una sola muestra o sobre la diferencia de proporciones en dos muestras. Se calcula el estadístico de prueba y el valor p para la hipótesis nula de que la probabilidad de éxito en una sola muestra es igual a p o que la diferencia de probabilidades de éxito en dos muestras es igual a 0. Se calcula un intervalo de confianza para la probabilidad de éxito en una sola muestra o para la diferencia de probabilidades de éxito en dos muestras.
Pueden usarse solo grupos con números finitos de éxitos y fracasos. Los conteos de éxitos y fracasos deben ser no negativos y, por lo tanto, no mayores que los números correspondientes de ensayos que deben ser positivos. Todos los conteos finitos deben ser enteros.
Si
pes NULL y hay más de un grupo, la hipótesis nula probada es que las proporciones en cada grupo son las mismas. Si hay dos grupos, las alternativas son que la probabilidad de éxito en el primer grupo es menor que, no igual a, o mayor que la probabilidad de éxito en el segundo grupo, según lo especificado por “alternative”.Si hay más de dos grupos, la alternativa es siempre “two.sided”, el intervalo de confianza devuelto es NULL y la corrección de continuidad nunca se usa.
Un intervalo de confianza para la diferencia de proporciones con un nivel de confianza especificado por “conf.level” y recortado a [-1,1] se devuelve. La corrección de continuidad se usa solo si no excede la diferencia de proporciones de la muestra en valor absoluto. De lo contrario, si hay más de 2 grupos, la alternativa es siempre “two.sided”, el intervalo de confianza devuelto es NULL y la corrección de continuidad nunca se usa.
Si hay un único grupo, entonces la hipótesis nula probada es que la probabilidad subyacente de éxito es p, o .5 si p no se da. La alternativa es que la probabilidad de éxito es menor que, no igual a, o mayor que p o 0.5, respectivamente, según lo especificado por “alternative”. Se devuelve un intervalo de confianza para la proporción subyacente con un nivel de confianza especificado por “conf.level” y recortado a [0,1]. La corrección de continuidad se usa solo si no excede la diferencia de proporciones de la muestra en valor absoluto. El intervalo de confianza se calcula invirtiendo la prueba de puntuación.
Finalmente, si
pse da y hay más de 2 grupos, la hipótesis nula probada es la que las probabilidades subyacentes de éxito son las dadas porp. La alternativa es siempre “two.sided”, el intervalo de confianza devuelto es NULL y la corrección de continuidad nunca se usa.
17 Regresión lineal básica
17.1 Referencias didácticas
-
Aplicación didáctica-interactiva para realizar manipulaciones con la Regresión Lineal: “Explore Linear Regression”
En esta aplicación permite seleccionar los datos de varias fuentes (subirlos, añadirlos sobre la aplicación y ejemplos): Linear Regression
Obtiene los cálculos detallados sobre un modelo de regresión lineal simple “Statistics 202 - Simple linear regression”
Sobre Regresión Múltiple o Multivariante. Aplicación didáctica-interactiva para explorar relaciones sobre un dataset con múltiples variables: “Multivariate Relationships”
17.2 Gráficos muestran relaciones
17.3 Generación de datos sobre Regresión
17.3.1 Modelos de Regresión Lineal
# Establecer la semilla para reproduc
set.seed(123)
# Generar datos con heterocedasticidad
x <- rnorm(100, mean = 2, sd = 0.5) # Variable independiente
u <- rnorm(100, mean = 0, sd = 3 * x) # error
y <- 2 + 3 * x + u # Variable respuesta
# Crear un data.frame con los datos
data <- data.frame(x, y)
head(data) x y
1 1.719762 3.494096
2 1.884911 9.107343
3 2.779354 8.281130
4 2.035254 5.983750
5 2.064644 2.299671
6 2.857532 10.186593# Mis Libros: CRC.Learning.Microeconometrics.with.R.0367255383.pdf (pag. 28)
set.seed(123456789)
N <- 1000
a <- 2
b <- 3
c <- 4
u_x <- rnorm(N)
alpha <- 0 # no interviene "u_x"
x <- (1 - alpha)*runif(N) + alpha*u_x # Variable independiente
w <- (1 - alpha)*runif(N) + alpha*u_x # Variable independiente
u <- rnorm(N) # Error
y <- a + b*x + c*w + u # Variable respuesta
#lm1 <- lm(y ~ x)
#lm2 <- lm(y ~ x + w)# Dependencia entre x e y
alpha <- 0.5 # interviene "u_x" y provoca dependencia entre x e w
x <- (1 - alpha)*runif(N) + alpha*u_x # Variable independiente
w <- (1 - alpha)*runif(N) + alpha*u_x # Variable independiente
y <- a + b*x + c*w + u # Variable respuesta
# lm3 <- lm(y ~ x)
# lm4 <- lm(y ~ x + w)
# lm4b <- lm(y ~ x + w + x*w)# Establecer una semilla para reproducibilidad
set.seed(123)
# Generar datos simulados con relaciones lineales y correlaciones
publicidad <- runif(100, min=1000, max=5000) # Gastos en publicidad
ubicacion <- as.numeric(factor(sample(c('Centro', 'Suburbio', 'Rural'), 100, replace=TRUE))) # Ubicación de la tienda codificada numéricamente
satis_cliente <- rnorm(100, mean=7, sd=1.5) # Calificaciones de satisfacción del cliente
dias_ultima_promo <- sample(1:30, 100, replace=TRUE) # Días desde la última promoción
comp_cerca <- sample(c(0, 1), 100, replace=TRUE) # Presencia de competencia cercana (0 = No, 1 = Sí)
# Crear una variable de ventas que dependa de las otras variables
ventas <- 150 + 0.3*publicidad - 15*ubicacion + 8*satis_cliente - 0.5*dias_ultima_promo - 20*comp_cerca + rnorm(100, mean=0, sd=10)
# Añadir una correlación entre publicidad y dias_ultima_promo
dias_ultima_promo <- dias_ultima_promo + 0.2*publicidad
# Crear un data.frame con los datos generados
datos_simulados <- data.frame(ventas, publicidad, ubicacion, satis_cliente, dias_ultima_promo, comp_cerca)
# Ver los primeros registros del data.frame
head(datos_simulados) ventas publicidad ubicacion satis_cliente dias_ultima_promo comp_cerca
1 834.6130 2150.310 1 7.176470 449.0620 0
2 1357.8673 4153.221 3 5.578788 855.6441 1
3 953.7231 2635.908 1 6.264164 545.1815 1
4 1508.4396 4532.070 3 6.615862 923.4139 0
5 1625.0167 4761.869 1 9.765793 958.3738 1
6 531.1996 1182.226 2 6.022075 246.4452 0# Instalar paquetes necesarios si no están instalados
if (!require("MASS")) install.packages("MASS", dependencies = TRUE)
library(MASS)
# Establecer la semilla para reproducibilidad
set.seed(123)
# Generar datos con multicolinealidad usando la función mvrnorm
# Supongamos que tenemos 3 variables predictoras y una variable de respuesta
# Las variables predictoras tienen una alta correlación entre sí
# Crear una matriz de correlación
correlation_matrix <- matrix(c(1, 0.9, 0.9, 0.9, 1, 0.9, 0.9, 0.9, 1), nrow = 3)
# Generar datos
data <- mvrnorm(n = 100, mu = c(0, 0, 0), Sigma = correlation_matrix)
# Convertir a dataframe y añadir una variable de respuesta
data <- as.data.frame(data)
colnames(data) <- c("Predictor1", "Predictor2", "Predictor3")
data$Response <- with(data, 3 + 2 * Predictor1 + 2 * Predictor2 + 2 * Predictor3 + rnorm(100))
# Ver las primeras filas del dataframe
head(data) Predictor1 Predictor2 Predictor3 Response
1 -0.19802316 -0.2906963 -1.13569326 -0.9640677
2 0.08830443 -0.2472094 -0.50821281 0.9130755
3 1.41285612 1.5607991 1.54391069 11.0965931
4 0.12626040 0.1741640 -0.09607171 2.3561922
5 -0.10829059 0.3558603 0.12714172 3.3122634
6 1.55165152 1.6535718 1.76550728 13.2726403# Instalar paquetes necesarios si no están instalados
if (!require("MASS")) install.packages("MASS", dependencies = TRUE)
library(MASS)
# Establecer la semilla para reproducibilidad
set.seed(123)
# Generar datos con multicolinealidad oculta
# Supongamos que tenemos 4 variables predictoras y una variable de respuesta
# Las variables predictoras tienen bajas correlaciones lineales entre sí
# pero hay multicolinealidad debido a una combinación lineal
# Crear una matriz de correlación con bajas correlaciones
correlation_matrix <- matrix(c(1, 0.1, 0.1, 0.1,
0.1, 1, 0.1, 0.1,
0.1, 0.1, 1, 0.1,
0.1, 0.1, 0.1, 1), nrow = 4)
# Generar datos
data <- mvrnorm(n = 100, mu = c(0, 0, 0, 0), Sigma = correlation_matrix)
# Convertir a dataframe y añadir una variable de respuesta
data <- as.data.frame(data)
colnames(data) <- c("Predictor1", "Predictor2", "Predictor3", "Predictor4")
data$Response <- with(data, 3 + 2 * Predictor1 + 2 * (Predictor2 - Predictor3) + rnorm(100))
# Ver las primeras filas del dataframe
head(data) Predictor1 Predictor2 Predictor3 Predictor4 Response
1 -1.0461394 -0.4520644 -1.3649455 1.5850682 2.6599274
2 -0.1046585 -0.7556167 -0.7126985 1.0480883 1.5361952
3 0.4750974 0.3837525 1.5256407 1.1699113 1.0316701
4 -0.4793640 -0.4917366 0.2015566 0.9303279 0.6258441
5 -0.7779714 0.2424742 0.6931070 0.1372116 1.2134877
6 1.0196129 1.2196414 1.1553239 0.5163717 3.5173142# Establecer la semilla para reproducibilidad
set.seed(123)
# Generar variables numéricas significativas
num_var1 <- rnorm(100) # Variable numérica normal
num_var2 <- runif(100, min = 50, max = 100) # Variable numérica uniforme
num_var3 <- sample(1:10, 100, replace = TRUE) # Variable numérica entera
num_var4 <- rpois(100, lambda = 3) # Variable numérica de Poisson
num_var5 <- rexp(100, rate = 0.1) # Variable numérica exponencial
num_var6 <- rbinom(100, size = 1, prob = 0.5) # Variable numérica binomial
# Generar variables numéricas poco significativas
num_var7 <- rnorm(100, mean = 0, sd = 10) # Variable numérica con alta varianza
num_var8 <- runif(100, min = -10, max = 10) # Variable numérica con rango amplio
# Generar variables de factor significativas
factor_var1 <- factor(sample(c("Categoría 1", "Categoría 2"), 100, replace = TRUE))
factor_var2 <- factor(sample(c("Grupo A", "Grupo B", "Grupo C"), 100, replace = TRUE))
# Generar variables de factor poco significativas
factor_var3 <- factor(sample(c("Nivel 1", "Nivel 2"), 100, replace = TRUE))
factor_var4 <- factor(sample(c("Tipo X", "Tipo Y", "Tipo Z", "Tipo W"), 100, replace = TRUE))
# Crear interacciones entre variables
interaction1 <- num_var1 * num_var3
interaction2 <- num_var2 * as.numeric(factor_var1)
# Generar la variable de respuesta con una combinación lineal de las predictoras e interacciones
response <- 5 + 1.5 * num_var1 + 2 * num_var2 + 0.5 * num_var3 +
3 * as.numeric(factor_var1) + 2 * as.numeric(factor_var2) +
interaction1 + interaction2 + rnorm(100)
# Función para añadir outliers a una variable numérica
add_outliers <- function(variable, amount, multiplier = 3) {
# Identificar los índices para los outliers
indices <- sample(1:length(variable), amount, replace = TRUE)
# Calcular el valor de los outliers
outliers <- mean(variable) + multiplier * sd(variable)
# Añadir outliers a la variable
variable[indices] <- outliers
return(variable)
}
# Función para añadir valores faltantes a una variable
add_missing_values <- function(variable, amount) {
# Identificar los índices para los valores faltantes
indices <- sample(1:length(variable), amount, replace = TRUE)
# Añadir valores faltantes a la variable
variable[indices] <- NA
return(variable)
}
# Aplicar las funciones a las variables numéricas
num_var1 <- add_outliers(num_var1, 5)
num_var1 <- add_missing_values(num_var1, 5)
# Repetir para las demás variables numéricas...
# Aplicar las funciones a las variables de factor
factor_var1 <- as.character(factor_var1)
factor_var1 <- add_missing_values(factor_var1, 5)
factor_var1 <- factor(factor_var1)
# Repetir para las demás variables de factor...
# Crear el dataframe con las variables modificadas
data <- data.frame(response, num_var1, num_var2, num_var3, num_var4, num_var5, num_var6,
num_var7, num_var8, factor_var1, factor_var2, factor_var3, factor_var4,
interaction1, interaction2)# Establecer la semilla para reproducibilidad
set.seed(123)
# Funciones previamente definidas para añadir outliers y missing values
# ...
# Generar una variable confusora que esté correlacionada con num_var1 y num_var2
confounder <- 0.3 * num_var1 + 0.5 * num_var2 + rnorm(100, mean = 0, sd = 1)
# Ajustar la variable de respuesta para incluir el efecto de la variable confusora
data$response <- data$response + 1.2 * confounder
# Añadir la variable confusora al dataframe
data$confounder <- confounder
# Crear un modelo de regresión lineal incluyendo la variable confusora
# model <- lm(response ~ num_var1 + num_var2 + confounder, data = data)
# Resumen del modelo para ver el efecto de la confusión
# summary(model)17.3.2 Modelos de Regresión Logística
set.seed(12345)
n = 1000
x = rnorm(n) # Variable independiente
z = sample(0:1, n, replace = TRUE) # Variable independiente
u = rnorm(n) # Error
# Variable categórica que no interviene en modelo pero se incluye en los datos
cat = as.factor(sample(c("cat1", "cat2", "cat3"), n, replace = TRUE))
# resultado binario
y = ifelse(pnorm(1 + 0.5*x - 0.5*z + u)>0.5, 1, 0) # Variable Respuesta
datos = data.frame(y,x,z,cat)
head(datos) y x z cat
1 1 0.5855288 0 cat3
2 1 0.7094660 1 cat1
3 1 -0.1093033 1 cat1
4 1 -0.4534972 0 cat1
5 0 0.6058875 1 cat2
6 0 -1.8179560 0 cat1# a<-glm(y ~ x + z + cat, data = datos, family = binomial('logit'))
# summary(a)17.4 Regresión Lineal Simple
datos2C = data.frame(X=c(3,2,4,2,1,2,5,2,3,2),
Y=c(2,5,4,3,3,4,4,3,2,3))
ggplot(datos2C) +
geom_point(aes(x=X, y=Y), color="blue") (reglin1var = lm(datos2C$Y ~ datos2C$X))
Call:
lm(formula = datos2C$Y ~ datos2C$X)
Coefficients:
(Intercept) datos2C$X
3.04839 0.09677 Mejor:
X = datos2C$X
Y = datos2C$Y
(reglin1 = lm(Y ~ X))
Call:
lm(formula = Y ~ X)
Coefficients:
(Intercept) X
3.04839 0.09677 summary(reglin1)
Call:
lm(formula = Y ~ X)
Residuals:
Min 1Q Median 3Q Max
-1.3387 -0.2419 -0.1935 0.5403 1.7581
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.04839 0.80241 3.799 0.00524 **
X 0.09677 0.28369 0.341 0.74180
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.999 on 8 degrees of freedom
Multiple R-squared: 0.01434, Adjusted R-squared: -0.1089
F-statistic: 0.1164 on 1 and 8 DF, p-value: 0.7418Con plot() del sistema base:
Con ggplot2:
ggplot(datos2C) +
geom_point(aes(x=X, y=Y), color="blue") +
geom_smooth(aes(x=X, y=Y), method="lm", se=FALSE, color="red")(reglin1_xsobrey = lm(X ~ Y))
Call:
lm(formula = X ~ Y)
Coefficients:
(Intercept) Y
2.1111 0.1481 summary(reglin1_xsobrey)
Call:
lm(formula = X ~ Y)
Residuals:
Min 1Q Median 3Q Max
-1.5556 -0.6667 -0.5556 0.5926 2.2963
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.1111 1.4855 1.421 0.193
Y 0.1481 0.4343 0.341 0.742
Residual standard error: 1.236 on 8 degrees of freedom
Multiple R-squared: 0.01434, Adjusted R-squared: -0.1089
F-statistic: 0.1164 on 1 and 8 DF, p-value: 0.7418Con plot() del sistema base:
Con ggplot2:
ggplot(datos2C) +
geom_point(aes(x=X, y=Y), color="blue") +
geom_smooth(aes(x=Y, y=X), method="lm", se=FALSE, color="red")(coef.r = cor(datos2C$X,datos2C$Y)) # cor(X,Y)[1] 0.1197369(coef.determinacion = coef.r^2)[1] 0.01433692Nota: puede observarse que en el resumen o summary del modelo lineal aparece el coeficiente de determinación en el apartado (redondeado a 5 cifras decimales):
Multiple R-squared: 0.01434Predecir el valor de la variable Y a partir de un valor de la variable X
predict(reglin1,newdata = data.frame(X=6)) 1
3.629032 # reglin1$coefficients[1] + reglin1$coefficients[2] * 6Predecir el valor de la variable X a partir de un valor de la variable Y
predict(reglin1_xsobrey,newdata = data.frame(Y=1)) 1
2.259259 Nota: También se podrían haber obtenido las predicciones sustituyendo los valores en las rectas de regresión correspondientes.
17.5 Ejercicios de Regresión Lineal
17.5.1 Ejercicio Regresión Lineal 1
En un proceso de fabricación se analizan dos variables cuantitativas X y Y, obteniéndose los siguientes resultados: (0,2), (1,6), (3,14), (-1,-2) y (2,10).
Calcule:
Las distribuciones marginales
La distribución de las frecuencias relativas de X para valores de “Y > 2.5”.
El coeficiente de correlación lineal de ambas variables.
Los valores de X e Y para las siguientes observaciones: (-3,y) y (x,4).
17.5.2 Ejercicio de Regresión Lineal 2
Dada la siguiente distribución bidimensional de frecuencias: \[ \begin{array}{|c|c|c|c|} \hline X/Y & 0 & 1 & 2 \\ \hline 0 & 15 & 15 & 10 \\ \hline 1 & 5 & 20 & 5 \\ \hline 2 & 10 & 5 & 15 \\ \hline \end{array} \] Se pide calcular:
La media aritmética y la varianza de la variable \(X-Y\).
La recta de regresión de Y sobre X y la varianza residual de Y.